6. Свободные затухающие колебания в реальном колебательном контуре

6.1. Основные формулы и обозначения

Вреальном колебательном контуре (рис. 8) колебания заряда являются затухающими:, где– частота свободных затухающих колебаний;– коэффициент затухания. Средняя за период полная энергия, логарифмический декремент затухания, добротность вычисляются по формулам (84) – (88). Рис. 8

6.2. Примеры решения задач

14. Колебательный контур состоит из конденсатора емкостью 0,8 мкФ, катушки индуктивностью 1,25 мГн и сопротивления. Найти: 1) сопротивление контура, при котором за 14 мс амплитуда колебаний заряда на обкладках конденсатора уменьшается в 1,7 раза; 2) логарифмический декремент затухания.

Дано: Ф; Гн. с; . Найти: ;.

Решение. Сопротивление связано с коэффициентом затухания колебаний и индуктивностью контура: (103) Для определения воспользуемся выражением (104) для расчета амплитуды затухающих колебаний.

Отсюда для интересующего момента времени получим:и выразим:

(105)

Объединив формулы (105) и (103), получим:

(106)

Подстановка численных данных приводит к следующему результату: .

Логарифмический декремент затухания

(107)

где – период затухающих колебаний, связанный с их циклической частотой

(108)

соотношением:

; (109)

– (110)

собственная частота колебаний в контуре.

Для того, чтобы найти приравняем друг другу квадраты периодаиполученные из формул (107) и (109):

(111)

а затем в выражение (111) подставим формулы для частот (108) и (110): . Отсюда, учитывая равенство (105), выразим:

(112)

Подставив в формулу (112) данные задачи, получим: .

Ответ: ,;

.

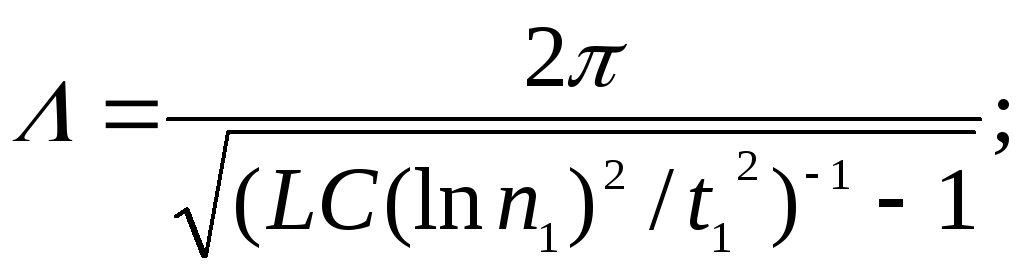
З а д а ч а 15. В реальном колебательном контуре напряжение на обкладках конденсатора меняется по закону: гдеВ;с^-1; с^-1; . Найти: 1) период собственных колебаний в контуре, если его индуктивность равна 0,85 Гн; 2) энергию электрического поля спустя время, равное 1/6 периода от начала затухающих колебаний.

Дано: ; с-1; с-1; ;Гн; . Найти: ;

Решение. Период собственных колебаний . (113) Собственная частота связана с циклической частотой затухающих колебаний соотношением:

из которого следует, что

(114)

следовательно, Подставив в полученное выражение данные задачи, получим:с.

Электрическая емкость контура выражается из равенствадля собственной частоты колебаний в контуре:

, (115)

где при переходе к правой части использовано соотношение (114).

Подставив в зависимость энергии электрического поля от времени (см. равенство (51))

(116)

выражение (115) и закон колебаний напряжения, заданный в условии, получим:

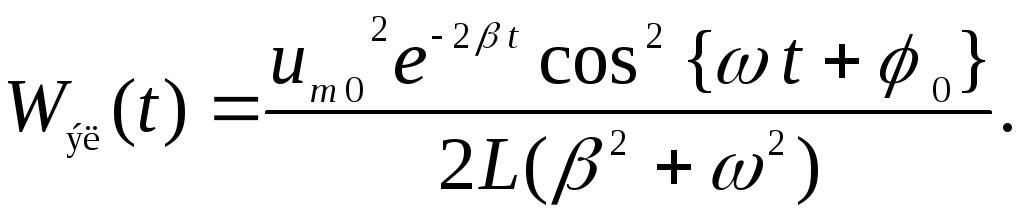(117)

Так как ,, а, в момент времениэнергия электрического поля

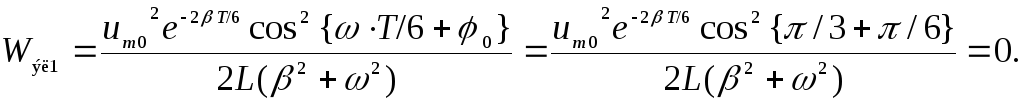
Ответ: ,с;

.

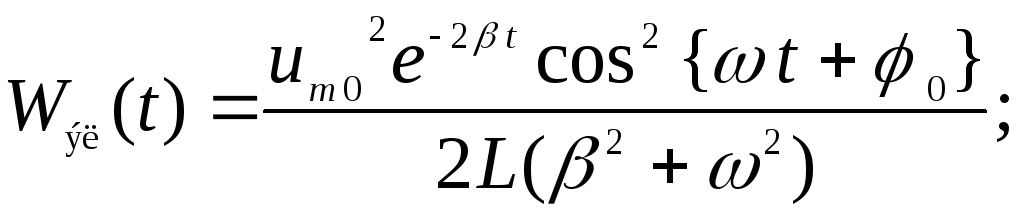
7. Вынужденные механические колебания1

7.1. Основные формулы и обозначения

Гармоническая вынуждающая сила задается выражением: в котороми– амплитуда и циклическая частота колебаний этой силы соответственно.

Закон вынужденных гармонических колебаний при установившемся движении имеет вид:

(118)

где

– (119)

амплитуда;

–разность фаз между колебанием и вынуждающей силой (),

(120)

Резонансная частота

(121)

резонансная амплитуда

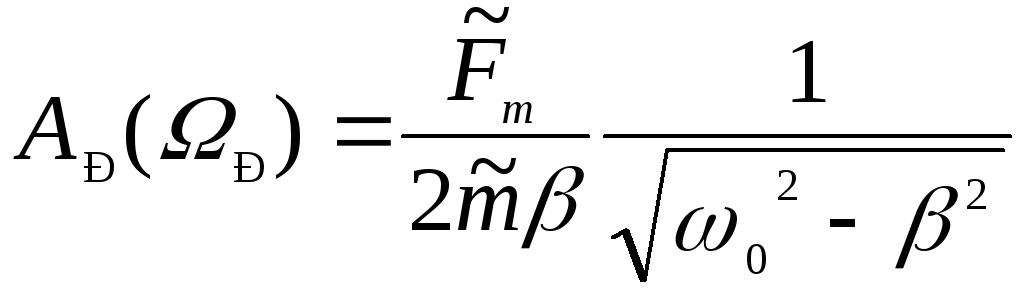. (122)