
- •Введение
- •1. Частота и период свободных незатухающих колебаний
- •1.1. Основные формулы и обозначения
- •1.2. Примеры решения задач
- •2. Свободные незатухающие механические колебания
- •2.1. Основные формулы и обозначения
- •2.2. Примеры решения задач
- •3. Свободные незатухающие колебания в идеальном колебательном контуре
- •3.1. Основные формулы и обозначения
- •3.2. Примеры решения задач
- •4. Сложение гармонических колебаний
- •4.1. Основные формулы и обозначения
- •4.2. Примеры решения задач
- •5. Свободные затухающие механические колебания
- •5.1. Основные формулы и обозначения
- •5.2. Примеры решения задач
- •6. Свободные затухающие колебания в реальном колебательном контуре
- •6.1. Основные формулы и обозначения
- •6.2. Примеры решения задач
- •7. Вынужденные механические колебания1
- •7.1. Основные формулы и обозначения
- •7.2. Примеры решения задач
- •8. Вынужденные колебания в колебательном контуре. Резонанс. Импеданс1
- •8.1. Основные формулы и обозначения
- •8.2. Примеры решения задач
- •9. Плоские монохроматические
- •9.1. Основные формулы и обозначения
- •9.2. Примеры решения задач
- •Библиографический список
- •644046, Г. Омск, пр. Маркса, 35
4. Сложение гармонических колебаний
4.1. Основные формулы и обозначения
П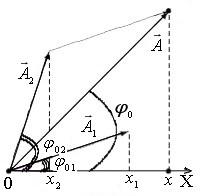 ри
сложении гармонических колебаний одного
направления и одинаковой частоты,
например, колебаний
ри
сложении гармонических колебаний одного
направления и одинаковой частоты,
например, колебаний
![]() и
и![]() удобно использовать метод векторных
диаграмм. Каждое колебание изображается
вектором на плоскости (например,
удобно использовать метод векторных
диаграмм. Каждое колебание изображается
вектором на плоскости (например,![]() и
и![]() ).
Длина этого вектора равна амплитуде
соответствующего колебания. Угол между
вектором и Рис. 5
горизонтальной осью равен фазе
соответствующего колебания в данный
момент времени. Вектор
).
Длина этого вектора равна амплитуде
соответствующего колебания. Угол между
вектором и Рис. 5
горизонтальной осью равен фазе
соответствующего колебания в данный
момент времени. Вектор![]() описывающий результирующее колебание,
строится по правилам сложения векторов.
Частота результирующего колебания
описывающий результирующее колебание,
строится по правилам сложения векторов.
Частота результирующего колебания![]() также равна
также равна![]() Амплитуда и начальная фаза результирующего
колебания определяются по диаграмме
для начального момента времени (рис. 5)
и вычисляются соответственно по формулам:
Амплитуда и начальная фаза результирующего
колебания определяются по диаграмме
для начального момента времени (рис. 5)
и вычисляются соответственно по формулам:
![]() (70)
(70)
![]() (71)
(71)
При сложении
гармонических взаимно перпендикулярных
колебаний,
совершаемых точкой в плоскости
![]() ,
например, колебаний
,
например, колебаний
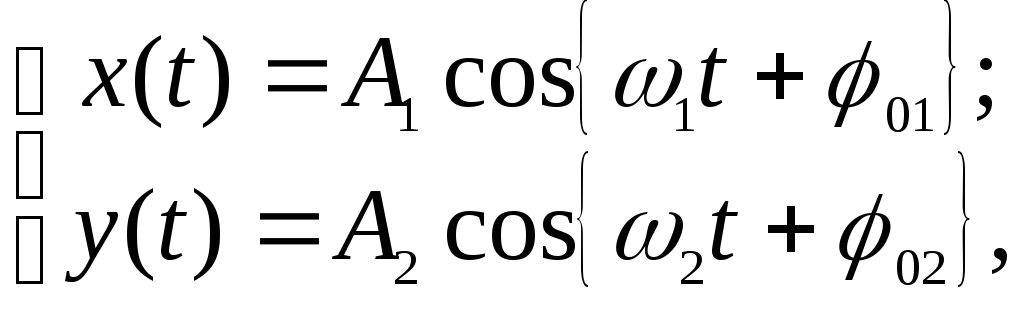 (72)
(72)
уравнение траектории
движения содержит только переменные
![]() и
и![]() но не содержит времени
но не содержит времени![]() Следовательно, уравнение траектории
можно найти, если каким-либо образом
исключить из формул (72) время, например,
выразить
Следовательно, уравнение траектории
можно найти, если каким-либо образом
исключить из формул (72) время, например,
выразить![]() через
через![]() или
или![]() .
.
Если при этом
отношение частот (периодов)
![]() является рациональной дробью (отношением
целых чисел), то траектория оказывается
замкнутой, а движение – периодическим.
является рациональной дробью (отношением
целых чисел), то траектория оказывается
замкнутой, а движение – периодическим.
4.2. Примеры решения задач
З а д а ч а 10.
Построить векторную диаграмму в начальный
момент времени при сложении двух
гармонических колебаний одинаковой
частоты и одного направления. Найти
графически и аналитически амплитуду и
начальную фазу результирующего колебания.
Записать закон результирующего колебания.
Законы складываемых колебаний имеют
вид:
![]()
![]() где
где![]() см;
см;![]() см;
см;![]() с-1;
с-1;
![]()
![]()
|
Дано:
Найти:
|
Решение.
Чтобы найти
амплитуду и начальную фазу результирующего
колебания, можно воспользоваться
формулами (70), (71), предварительно
заменив по формуле приведения
|
где
![]() .
(74)
.
(74)
Тогда
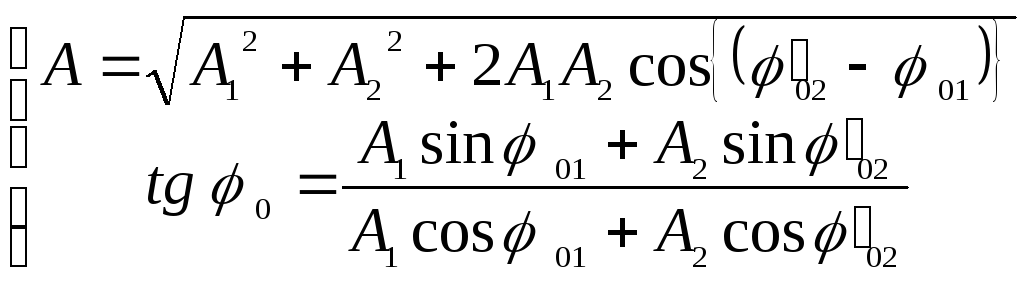 .
(75)
.
(75)
Подставляя в
равенства (75) численные данные и учитывая
формулу (74), получим:
![]() см;
см;![]() Отсюда
Отсюда![]() °
°![]() рад.
Следовательно, закон результирующего
колебания имеет вид:
рад.
Следовательно, закон результирующего
колебания имеет вид:![]() где
где![]() см;
см;![]() с-1;
с-1;
![]() рад.
рад.
Начертим векторную
диаграмму сложения колебаний в начальный
момент времени (рис. 6). Для этого в
соответствии с правилами построения,
изложенными в подразделе 4.1, сопоставим
колебанию
![]() вектор
вектор![]() длиной
длиной![]() ,
который направим под углом
,
который направим под углом![]() к горизонтальной оси
к горизонтальной оси![]() ,
т. е. вертикально вверх; колебанию
,
т. е. вертикально вверх; колебанию![]() сопоставим вектор
сопоставим вектор![]() длиной
длиной![]() ,
который направим под углом
,
который направим под углом![]() к горизонтальной оси
к горизонтальной оси![]() ,
т. е. отложим его в направлении оси (см.
рис. 6). Результирующее колебание будет
описываться вектором
,
т. е. отложим его в направлении оси (см.
рис. 6). Результирующее колебание будет
описываться вектором![]() длиной
длиной![]() полученным по правилу параллелограмма
сложением векторов
полученным по правилу параллелограмма
сложением векторов![]() и
и![]() Угол, образованный вектором
Угол, образованный вектором![]() и осью
и осью![]() равен начальной фазе результирующего
колебания
равен начальной фазе результирующего
колебания![]()
О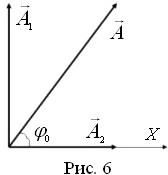 твет:
твет:![]() где
где![]() см;
см;![]() с-1;
Рис. 6
с-1;
Рис. 6
![]() рад.
рад.
З а д а ч а 11.
Получить уравнение траектории частицы
и построить траекторию в плоскости
![]() ,
если частица одновременно участвует в
двух взаимно перпендикулярных колебаниях:
,
если частица одновременно участвует в
двух взаимно перпендикулярных колебаниях:![]()
![]() где
где![]() см,
см,![]() см.
см.
|
Дано:
Найти:
|
Решение.
Чтобы найти
уравнение траектории точки
|
![]() ;
(76)
;
(76)
![]() (77)
(77)
исключить время.
Для этого из уравнения (76) выразим
![]() :
:
![]() . (78)
. (78)
Отсюда
![]() . (79)
. (79)
Преобразовав и возведя в квадрат уравнение (77), а затем, последовательно применив формулы приведения и двойного аргумента к тригонометрическим функциям, получим:
![]() . (80)
. (80)
Используя соотношения (78) и (79), из выражения (80) можно исключить время и получить уравнение траектории:
![]()
 (81)
(81)
Для построения
траектории в плоскости
![]() выберем наиболее удобные точки. Это
точки, имеющие равную нулю, наибольшую
и наименьшую из возможных ординату (
выберем наиболее удобные точки. Это
точки, имеющие равную нулю, наибольшую
и наименьшую из возможных ординату (![]() )
или абсциссу (
)
или абсциссу (![]() ).
).
|
Таблица 2 | |
|
|
|
|
|
|
|
|
|
(см. Табл. 2).
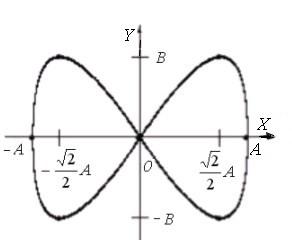
Траектория,
построенная по этим точкам, показана
на рис. 7. Координата
![]() достигает максимума по модулю четырежды,
а
достигает максимума по модулю четырежды,
а![]() – дважды. Это объясняется соответствующим
отношением частот: за время одного
колебания вдоль оси
– дважды. Это объясняется соответствующим
отношением частот: за время одного
колебания вдоль оси![]() точка совершает два колебания вдоль
оси
точка совершает два колебания вдоль
оси![]()
Ответ:
![]()
