2. Свободные незатухающие механические колебания

2.1. Основные формулы и обозначения

Закон гармонических колебаний является решением уравнения (1) и имеет вид¹:

(21)

или

(22)

где – колеблющаяся величина (обобщенная координата),

–время;

–амплитуда (обозначается также );

–фаза;

–начальная фаза;

–циклическая частота колебаний.

Проекции скорости и ускоренияна осьменяются также по гармоническому закону.

Потенциальная² и кинетическая энергия механических колебаний вычисляются по формулам:

; (23)

. (24)

Полная энергия колебаний не зависит от времени:

(25)

2.2. Примеры решения задач

З а д а ч а 3. Частица массой 14 г совершает свободные незатухающие колебания по закону синуса с периодом 3,7 с и с начальной фазой, равной нулю. Полная энергия колеблющейся частицы – 0,016 мДж. Найдите наибольшее значение модуля возвращающей силы, действующей на частицу.

Дано: кг; с; ; ; Дж. Найти: .

Решение. По условию зависимость координаты частицы от времени имеет вид: , (26) где – амплитуда; –время; – (27) собственная частота колебаний.

Согласно закону Гука проекция возвращающей силы, действующей на частицу, на ось вычисляется по формуле:

(28)

Так как движение одномерное, модуль силы

(29)

Следовательно, модуль возвращающей силы будет максимален при

(30)

Амплитуда колебаний может быть найдена, исходя из выражения (25) для полной энергии:

(31)

по формуле:

(32)

Объединив соотношение (3) и формулу (27), получим выражение для расчета обобщенного коэффициента жесткости:

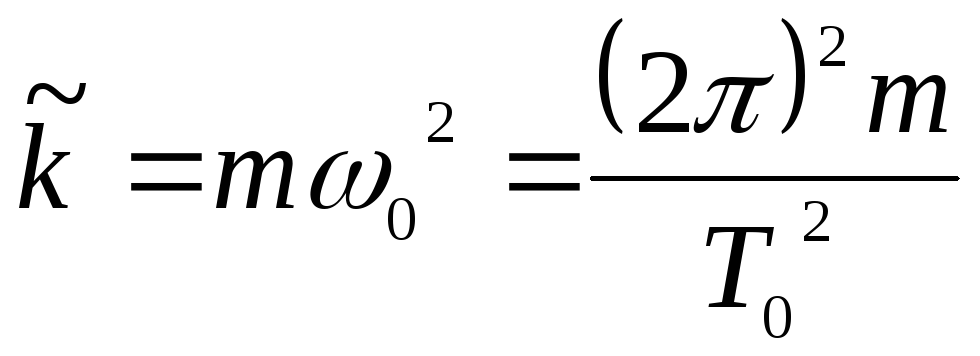. (33)

Подставив равенства (30) и (32), а затем – (33) в выражение (29), получим максимальное значение модуля возвращающей силы (другими словами, амплитуду колебаний силы): Отсюда после подстановки данных получим:.

Ответ: ,.

З а д а ч а 4. Математический маятник массой 250 г и длиной 1,2 м совершает гармонические колебания с амплитудой 72 мм. Определить: 1) полную энергию колебаний; 2) модуль скорости колебаний в момент времени, когда смещение маятника от положения равновесия равно 36 мм.

Дано: м; кг; м; м. Найти: ;

Решение. 1) Полную энергию колебаний маятника вычислим по формуле (25): , (34) подставив в нее соотношение (3) для обобщенного коэффициента жесткости

, (35)

а затем – выражение

(36)

для собственной частоты колебаний математического маятника:

(37)

Подставив в формулу (37) численные данные, получим: .

2) Колебания гармонические, поэтому выполняется закон сохранения энергии:

(38)

Полная энергия определяется выражением (37), а потенциальная и кинетическая – формулами (23), (24), следовательно, с учетом равенств (35) и (36)

(39)

Отсюда в момент времени

. (40)

Подставив в формулу (40) численные значения всех величин, получим: м/с.

Ответ: мДж;

, м/с.

З а д а ч а 5. Материальная точка совершает свободные гармонические колебания вдоль оси так, что проекция ее скорости на осьменяется с течением времени по закону:, гдем/с,рад/с,. Найти момент времени, ближайший к началу колебаний, когда проекция ускорения на ось колебаний равнам/с².

Дано: м/с; рад/с; м/с2. Найти:

Решение. Ускорение можно найти как производную по времени от скорости: (41) Выразим фазу колебаний из соотношения (41): , найдем время:

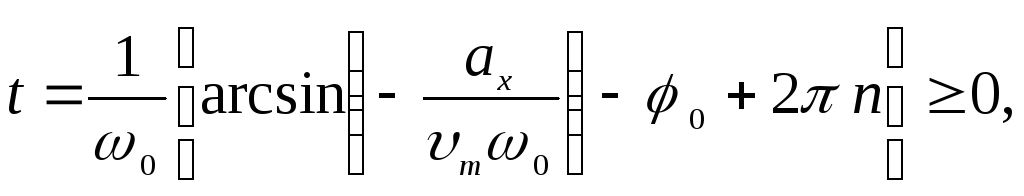(42)

где – целое.

Подстановка численных данных в правую часть формулы (42) приводит к ряду значений времени: распадающемуся на две последовательности, соответствующие двум значениям –и– функции:

с; (43)

с. (44)

Выбираем из всех возможных решений, представленных последовательностями (43) и (44), минимальное (ближайшее к нулю) положительное значение времени: с, которое получается при подстановке значенияв ряд (43).

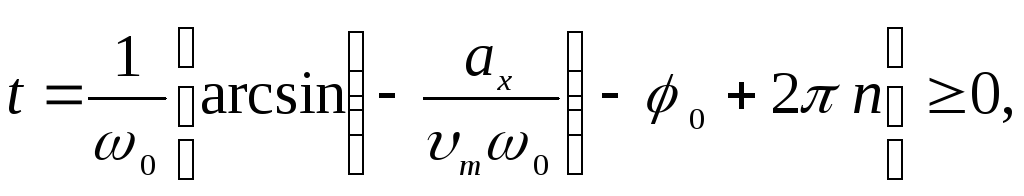
Ответ: с.

З а д а ч а 6. Горизонтальный пружинный маятник массой 170 г выводят из положения равновесия горизонтальным ударом по грузу, после которого маятник начинает совершать гармонические колебания с амплитудой 2 см. Записать закон колебаний и зависимость скорости колебаний от времени, если коэффициент упругости пружины равен 80 Н/м.

Дано: кг; м; Н/м; м. Найти: ;.

Решение. Так как маятник совершает гармонические колебания, зависимость его смещения от положения равновесия от времени в общем случае имеет вид: (45) где – начальная фаза;

с – (46)

собственная частота колебаний маятника.

Чтобы записать закон (45) для рассматриваемого в задаче пружинного маятника в явном виде, необходимо найти начальную фазу колебаний. Для этого подставим в закон начальное условие: (начальное условием означает, что в момент начала колебанийс маятник находился в положении равновесия), откуда

(47)

Подставив соотношение (45) и значение начальной фазы (47) в закон (45), получим зависимость:

(48)

Знак в правой части формулы (48) определяется выбором направления оси вдоль которой происходят колебания маятника. Если, например, направить осьв сторону смещения груза сразу после удара, то сразу после начала колебаний координата груза будет положительной, т. е. зависимость (48) примет вид:

(49)

где м;с.

Скорость колебаний можно найти как производную по времени от координаты, которая задана функцией (49):

(50)

Ответ: гдем,с;

гдем/с.