
- •Введение
- •1. Частота и период свободных незатухающих колебаний
- •1.1. Основные формулы и обозначения
- •1.2. Примеры решения задач
- •2. Свободные незатухающие механические колебания
- •2.1. Основные формулы и обозначения
- •2.2. Примеры решения задач
- •3. Свободные незатухающие колебания в идеальном колебательном контуре
- •3.1. Основные формулы и обозначения
- •3.2. Примеры решения задач
- •4. Сложение гармонических колебаний
- •4.1. Основные формулы и обозначения
- •4.2. Примеры решения задач
- •5. Свободные затухающие механические колебания
- •5.1. Основные формулы и обозначения
- •5.2. Примеры решения задач
- •6. Свободные затухающие колебания в реальном колебательном контуре
- •6.1. Основные формулы и обозначения
- •6.2. Примеры решения задач
- •7. Вынужденные механические колебания1
- •7.1. Основные формулы и обозначения
- •7.2. Примеры решения задач
- •8. Вынужденные колебания в колебательном контуре. Резонанс. Импеданс1
- •8.1. Основные формулы и обозначения
- •8.2. Примеры решения задач
- •9. Плоские монохроматические
- •9.1. Основные формулы и обозначения
- •9.2. Примеры решения задач
- •Библиографический список
- •644046, Г. Омск, пр. Маркса, 35
1.2. Примеры решения задач
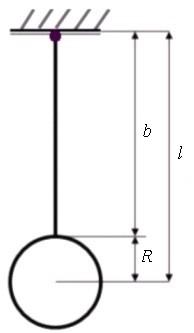
З а д а ч а 1. Маятник настенных часов можно представить в виде невесомого стержня длиной 30 см, к концу которого припаян диск радиусом 8 см и массой 2,5 кг (рис. 1). Маятник колеблется в вертикальной плоскости вокруг горизонтальной оси, проходящей через верхний конец стержня. Диск расположен в плоскости колебаний. Найти период малых свободных незатухающих колебаний маятника.
|
Дано:
Найти:
|
Решение. Тела, из которых сделан маятник, можно считать абсолютно твердыми, а маятник – физическим. Собственную частоту колебаний физического маятника можно найти по формуле:
в
которой
|
![]() –момент инерции
маятника,
–момент инерции
маятника,
![]() – (5)
– (5)
расстояние от
центра инерции до оси вращения;
![]() – ускорение свободного падения.
– ускорение свободного падения.
Период связан с циклической частотой соотношением:
![]() .
(6)
.
(6)
Подставив в соотношение (6) формулу (4), получим:
![]() .
(7)
.
(7)
Стержень невесом, поэтому масса и момент инерции маятника равны соответственно массе и Рис. 1 моменту инерции диска, который вычисляется с использованием теоремы Гюйгенса – Штейнера1, так как ось колебаний не проходит через центр инерции диска:
![]() ,
(8)
,
(8)
где
![]() – момент инерции диска относительно
оси,перпендикулярной
диску и проходящей через его центр.
– момент инерции диска относительно
оси,перпендикулярной
диску и проходящей через его центр.
С учетом равенств (5) и (8) выражение (7) принимает вид:
![]() .
(9)
.
(9)
Подставляем данные задачи:
![]() с.
с.
Ответ:
![]() ,
,![]() с.
с.
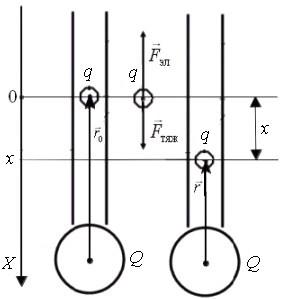
З а д а ч а 2. Маленькая заряженная дробинка может без трения двигаться внутри вертикально расположенной трубки, прикрепленной нижним концом к заряженному шару (рис. 2). Заряды шара и дробинки одноименные. Когда дробинка находится в состоянии равновесия, расстояние от нее до центра шара – 80 см. Найти собственную частоту малых вертикальных колебаний дробинки.
|
Дано:
Найти:
|
Решение. Собственная частота колебаний системы определяется по формуле:
где
|
Обобщенный коэффициент жесткости системы определяется в соответствии с законом Гука как коэффициент пропорциональности между возвращающей силой и обобщенной координатой:
![]() (11)
(11)
Обобщенная масса системы определяется как коэффициент пропорциональности между возвращающей силой и обобщенным ускорением:
![]() (12)
(12)
Таким образом,
основная цель при решении данной задачи
– найти эти обобщенные параметры,
используя явный вид возвращающей силы,
действующей на выведенный из положения
равновесия шарик. Для этого сначала
рассмотрим и найдем силы, действующие
на дробинку, находящуюся в состоянии
равновесия. Результирующая этих сил
равна нулю:
![]() так как при равновесии механической
системы все действующие на нее силы
скомпенсированы. Затем найдем
результирующую силу
так как при равновесии механической
системы все действующие на нее силы
скомпенсированы. Затем найдем
результирующую силу![]() действующую на дробинку, находящуюся
в неравновесном состоянии в положении
с координатой
действующую на дробинку, находящуюся
в неравновесном состоянии в положении
с координатой![]() Эта сила и будет возвращающей:
Эта сила и будет возвращающей:
![]()
 (13)
(13)
Считая дробинку
материальной точкой, направим ось
абсцисс
![]() вертикально, например, вниз, а в качестве
начала координат выберем положение
равновесия дробинки. Тогда координата
вертикально, например, вниз, а в качестве
начала координат выберем положение
равновесия дробинки. Тогда координата![]() дробинки Рис. 2 характеризует
ее смещение от положения равновесия,
т. е. является обобщенной координатой.
дробинки Рис. 2 характеризует
ее смещение от положения равновесия,
т. е. является обобщенной координатой.
В равновесии на
дробинку действуют две силы: сила тяжести
![]() направленная вертикально вниз, и
направленная в противоположную сторону
сила электрического отталкивания
направленная вертикально вниз, и
направленная в противоположную сторону
сила электрического отталкивания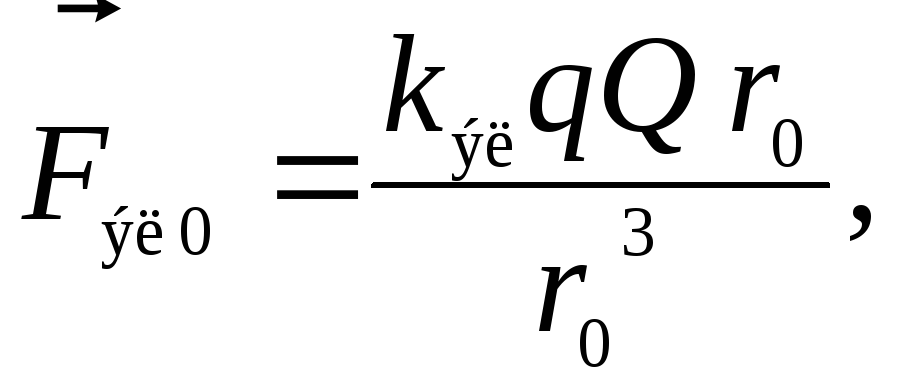 где
где![]() и
и![]() – заряды дробинки и шара соответственно,
вектор
– заряды дробинки и шара соответственно,
вектор![]() проведен из центра шара к дробинке (в
состоянии равновесия). Согласно принципу
суперпозиции сил
проведен из центра шара к дробинке (в
состоянии равновесия). Согласно принципу
суперпозиции сил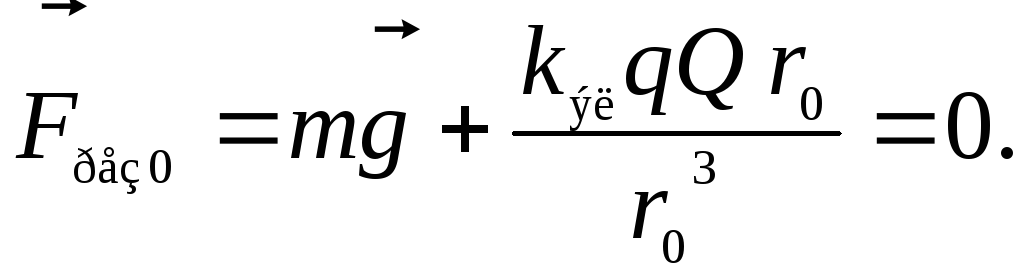 Следовательно, модули силы тяжести и
силы электрического отталкивания равны:
Следовательно, модули силы тяжести и
силы электрического отталкивания равны:
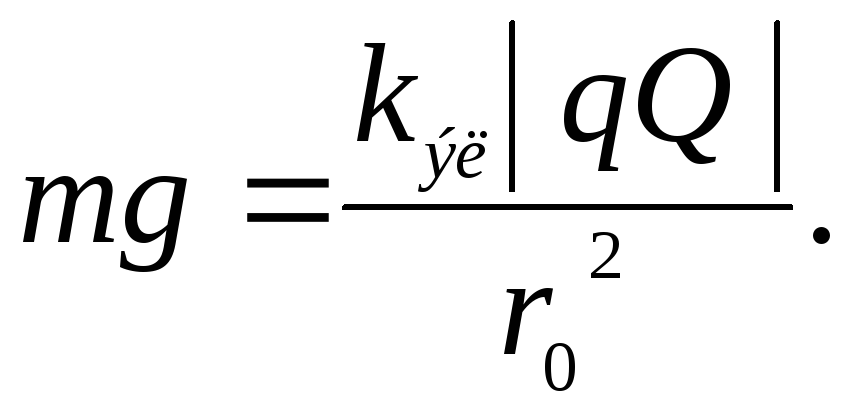 (14)
(14)
На выведенную из
равновесия дробинку действуют те же
две силы. Сила тяжести не меняется, а
сила электрического отталкивания
![]() изменяется: она уменьшается по модулю
в случае удаления дробинки от шара и
увеличивается в случае ее приближения
к шару. Вектор
изменяется: она уменьшается по модулю
в случае удаления дробинки от шара и
увеличивается в случае ее приближения
к шару. Вектор![]() проведен из центра шара к дробинке,
причем
проведен из центра шара к дробинке,
причем![]() Согласно принципу суперпозиции сил
результирующая сила
Согласно принципу суперпозиции сил
результирующая сила![]() Проекция
Проекция![]() на ось
на ось![]() рассчитывается по формуле:
рассчитывается по формуле:
![]() (15)
(15)
где
![]() при смещении дробинки вниз и
при смещении дробинки вниз и![]() при ее смещении вверх.
при ее смещении вверх.
При малых колебаниях
![]() ,
поэтому выражение
,
поэтому выражение![]() можно разложить в ряд по степеням
можно разложить в ряд по степеням![]() ,
ограничившись линейным приближением,
т. е., оставив только два первых слагаемых
ряда и пренебрегая остальными слагаемыми
в силу их малости относительно двух
первых1:
,
ограничившись линейным приближением,
т. е., оставив только два первых слагаемых
ряда и пренебрегая остальными слагаемыми
в силу их малости относительно двух
первых1:
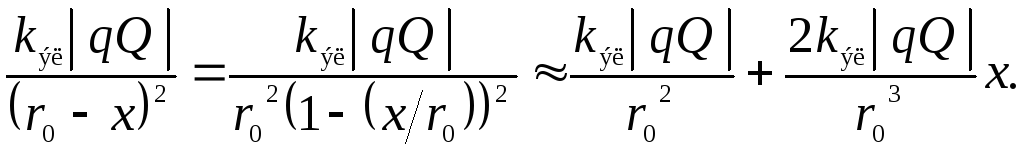 (16)
(16)
Подставив разложение (16) в формулу (15), получим:
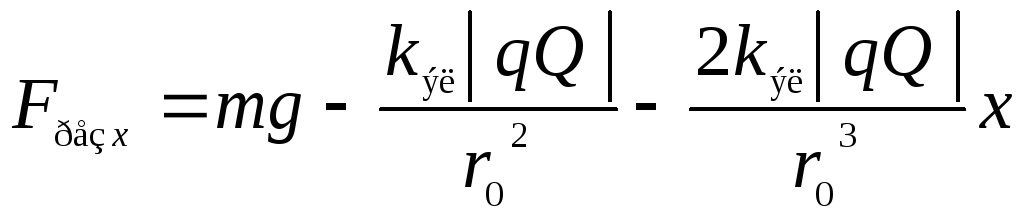 .
(17)
.
(17)
Объединяя равенства (14), (15) и (17), получим в явном виде выражение для расчета возвращающей силы:
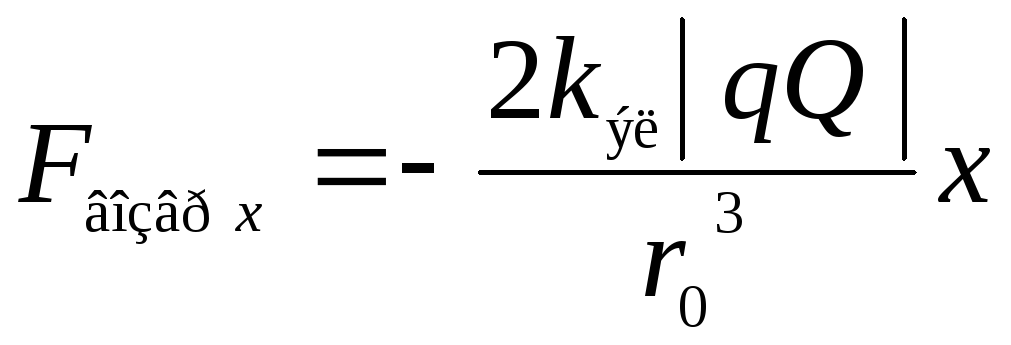 .
(18)
.
(18)
Сравнивая формулы
(18) и (11), найдем
![]()
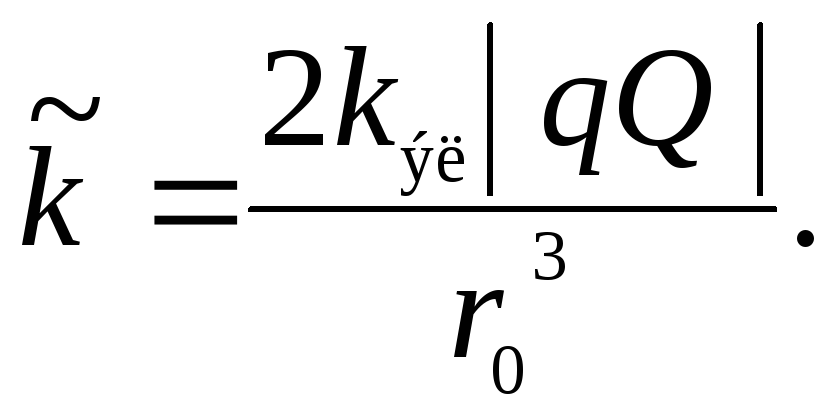 (19)
(19)
С учетом уравнения (14) выражение (19) упрощается и принимает вид:
![]() (20)
(20)
С другой стороны,
сравнив основное уравнение динамики
материальной точки для дробинки
![]() записанное с учетом равенства (13), с
выражением (12), заметим, что
записанное с учетом равенства (13), с
выражением (12), заметим, что![]() .
Используя равенство
.
Используя равенство![]() и выражение (20) для подстановки в формулу
(10), получим окончательное выражение
для собственной частоты:
и выражение (20) для подстановки в формулу
(10), получим окончательное выражение
для собственной частоты:![]() Подставляем в полученное выражение
данные задачи:
Подставляем в полученное выражение
данные задачи:![]() с-1.
с-1.
Ответ:
![]() ,
,![]() с-1.
с-1.
