
-resource-254-29254-files-samiit271
.pdf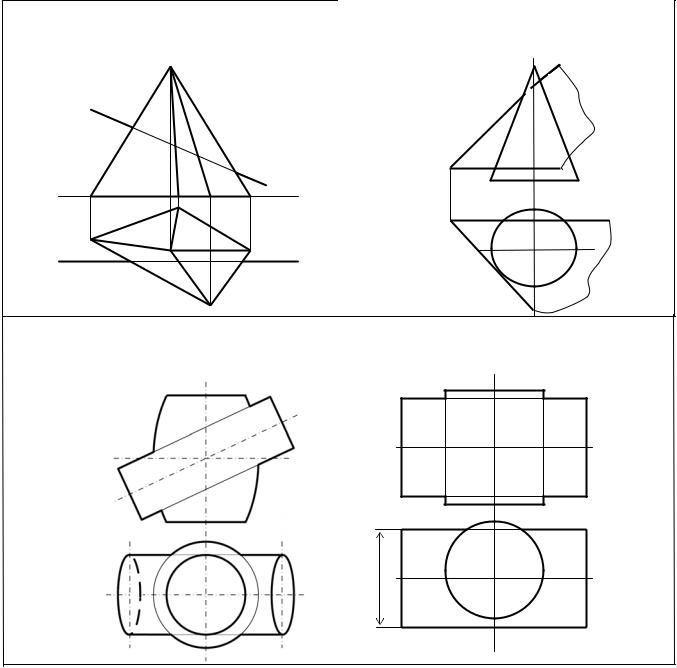
|
Вариант 48 |
|
|
Задача 1 |
|
Дано: |
прямая MN и точка А. |
|
Построить: |
ромб ABCD со стороной ВС на прямой MN, исходя из условия, что длина его стороны равна 1.2h. |
|
Определить углы наклона высоты к плоскостям проекций П1 и П2. M(190,10,20); N(0,100,20); А(200,70,80). |
||
|
Задача 2 |
|
Дано: |
плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK.. |
|
Построить: |
линию пересечения плоскостей. A(58,105,110); B(188,135,80); C(102,0,8), D(170,10,140), E(0,80,50), |
|
F(80,135,0) |
|
|
|
Задача 3 |
|
Дано: |
пирамида ABCS и точка D. |
|
Определить: |
высоту пирамиды и угол между гранью SAB и основанием АВС (способом замены плоскостей про- |
|
екций). Определить натуральный вид основания и совместить точку D с плоскостью BCS (вращением вокруг проеци- |
||
рующих осей). A(50,60,30); B(0,20,10); C(10,50,50); S(70,10,0); D(75,15,30). |
||
|
Задача 4 |
Задача 5 |
Найти точки пересечения прямой с поверхно- |
Построить линию пересечения фигуры с плос- |
|
стью. |
костью и дать полную развертку одной из ее частей. |
|
|
|
В2 |
|
а2 |
|
|
|
С2 |
|
|
А2 |
|
|
В1 |
|
|
А1 |
|
а1 |
|
|
|
С1 |
|
Задача 6 |
|
|
Построить линии пересечения поверхностей. |
|
Ø80
81

|
|
Вариант 49 |
|
|
Дано: |
прямая MN и точка А. |
Задача 1 |
|
|
|
|
|
||
Построить: |
ромб ABCD со стороной ВС на прямой MN, исходя из условия, что длина его стороны равна 1.2h. |
|||
Определить углы наклона высоты к плоскостям проекций П1 и П2. M(210,20,80); N(10,20,10); А(0,75,85). |
||||
|
|
Задача 2 |
|
|
Дано: |
плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK.. |
|||
Построить: |
линию пересечения плоскостей. |
A(210,0,65); |
B(45,130,55); C(92,0,0), |
D(115,20,120), E(0,20,35), |
F(100,110,13) |
|
|
|
|
Дано: |
пирамида ABCS и точка D. |
Задача 3 |
|
|
|
|
|
||
Определить: |
высоту пирамиды и угол между гранью SAB и основанием АВС (способом замены плоскостей про- |
|||
екций). Определить натуральный вид основания и совместить точку D с плоскостью ABC (вращением вокруг проеци- |
||||
рующих осей). A(20,60,30); B(80,20,10); C(70,50,50); S(10,10,0); D(90,60,25). |
|
|||
|
Задача 4 |
|
Задача 5 |
|
Найти точки пересечения прямой с поверхно- |
Построить линию пересечения фигуры с плос- |
|||
стью. А(35,140,5), В(110,45,95). |
костью и дать полную развертку одной из ее частей. |
|||
|
А2 |
|
B2 |
|
|
|
|
А2 |
|
|
В2 |
|
D2 |
|
|
|
|
С2 |
|
|
|
|
|
|
|
0 |
|
|
|
А1 |
|
|
B1 |
|
|
|
|
А1 |
|
|
|
|
|
С1 |
|
В1 |
|
D1 |
|
|
|
|
|
|
|
|
Задача 6 |
|
|
|
Построить линии пересечения поверхностей. |
|
||
Ø80
82
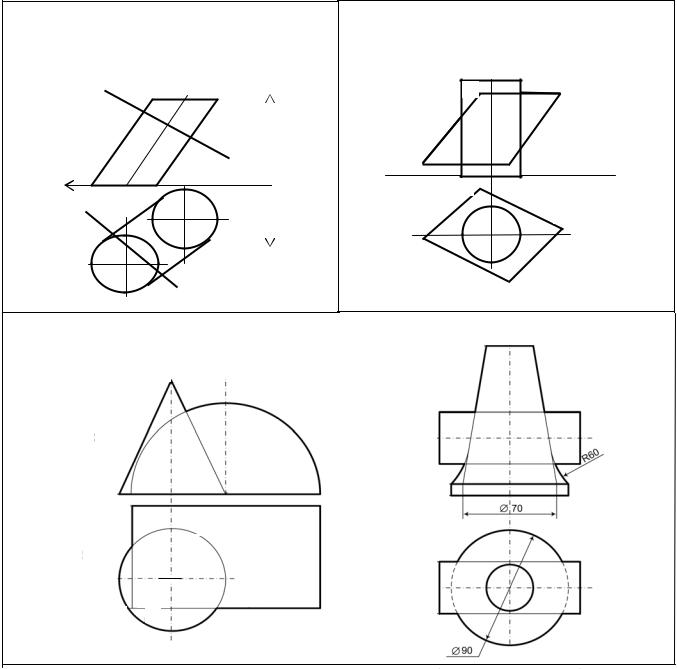
Вариант 50
Задача 1
Дано: прямая MN и точка А.
Построить: ромб ABCD со стороной ВС на прямой MN, исходя из условия, что длина его стороны равна 1.2h. Определить углы наклона высоты к плоскостям проекций П1 и П2. M(210,90,15); N(10,10,15); А(5,80,75).
Задача 2
Дано: плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK..
Построить: линию пересечения плоскостей. A(180,105,140); B(0,100,35); C(90,25,0), D(180,18,20), E(100,130,115), F(30,92,70)
Задача 3
Дано: пирамида ABCS и точка D.
Определить: высоту пирамиды и угол между гранью SAB и основанием АВС (способом замены плоскостей проекций). Определить натуральный вид основания и совместить точку D с плоскостью ABS (вращением вокруг проеци-
рующих осей). A(60,50,40); B(10,10,20); C(20,40,60); S(80,0,10); D(115,40,30).
Задача 4 |
|
Задача 5 |
Найти точки пересечения прямой АВ с поверх- |
Построить линию пересечения фигуры с плос- |
|
ностью цилиндра. А(115,38,100), В(30,150,0). |
костью и дать полную развертку одной из ее частей. |
|
А2 |
В2 |
С2 |
|
||
В2 |
А2 |
D2 |
|
||
0 |
В1 |
|
|
|
|
А1 |
С1 |
|
|
|
А1 |
В1 |
D1 |
Задача 6 Построить линии пересечения поверхностей.
83
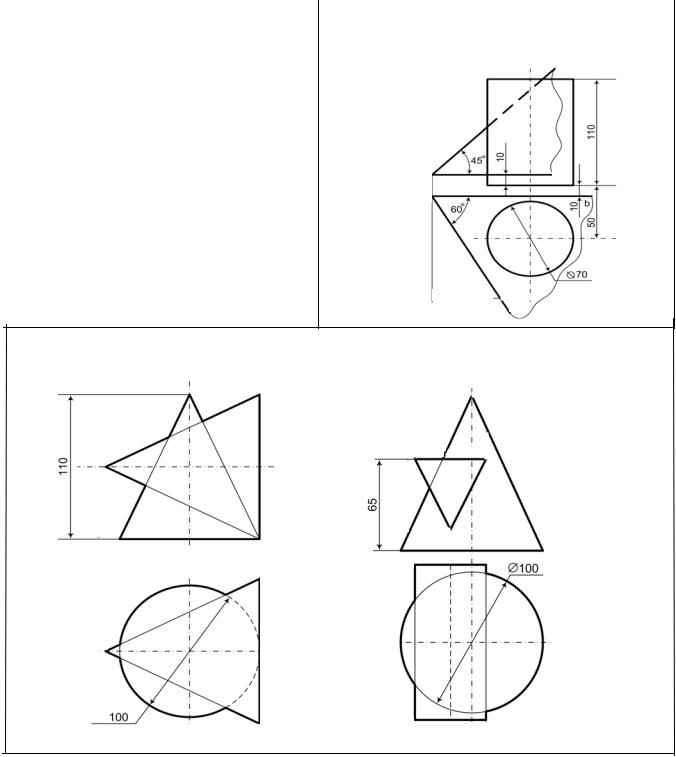
Вариант 51
Задача 1 Дано: прямая MN и одна проекция точек А и К.
Построить: параллелограмм ABCD с большей стороной ВС на прямой MN, исходя из условия, что точка К, основание высоты, делит ее в отношении 1:2 от точки В к точке С и угол В равен 60°. Определить углы наклона высоты к плоскостям проекций П1 и П2. M(180,10,20); N(0,10,100); А(190,60,-), К(130,10,-).
Задача 2
Дано: плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK..
Построить: линию пересечения плоскостей. A(210,10,108); B(0,42,25); C(125,128,25), D(100,0,10), E(30,15,42), F(138,128,110).
|
Задача 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дано: |
пирамида ABCS и точка D. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определить: |
высоту пирамиды и угол между |
|
|
|
|
Задача 5 |
||||||||||||||||||||
гранью SAB и основанием АВС (способом замены |
Построить линию пересечения фигуры с плоско- |
|||||||||||||||||||||||||
плоскостей проекций). Определить натуральный вид |
стью и дать полную развертку одной из ее частей. |
|||||||||||||||||||||||||
основания и совместить точку D с плоскостью ABS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
В2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(вращением вокруг проецирующих осей). A(0,20,0); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
B(80,10,20); C(40,0,50); S(30,40,20); D(100,50,20). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Задача 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти точки встречи прямой АВ с поверхностью |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
конуса (диаметр основания конуса 100). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A(10,35,135); |
B(150,105,28); |
О(90,60,10); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
С2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
S(90,60,130). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
А1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 С1
С1
Задача 6 Построить линии пересечения поверхностей.
84
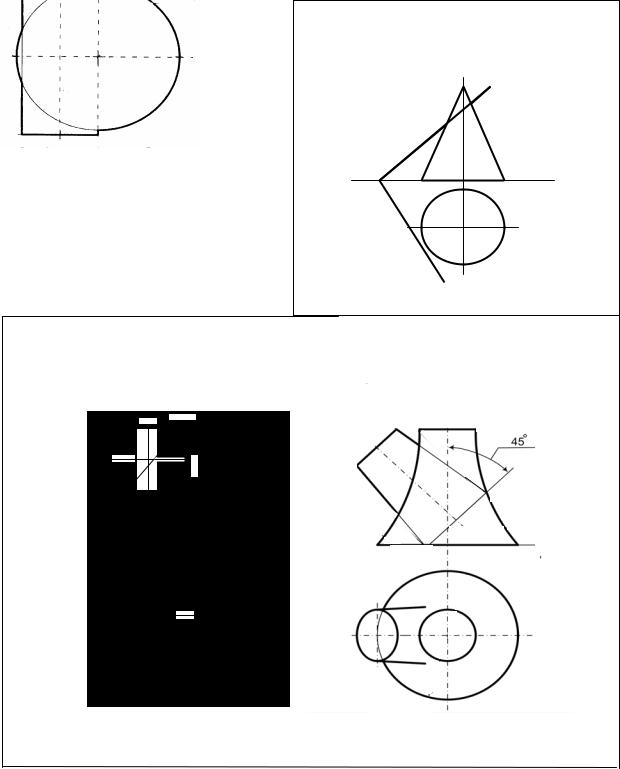
Вариант 52
Задача 1 Дано: прямая MN и одна проекция точек А и К.
Построить: параллелограмм ABCD с большей стороной ВС на прямой MN, исходя из условия, что точка К, основание высоты, делит ее в отношении 1:2 от точки В к точке С и угол В равен 60°. Определить углы наклона высоты к плоскостям проекций П1 и П2. M(200,10,90); N(30,10,20); А(30,50,-), К(70,10,-).
Задача 2
Дано: плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK..
Построить: линию пересечения плоскостей. A(130,125,115); B(0,60,60); C(188,10,10), D(30,30,80), E(10,90,20), F(188,90,10).
Задача 3
Дано: пирамида ABCS и точка D. Определить: высоту пирамиды и угол между гранью SAB и основанием АВС (способом замены плоскостей проекций). Определить натуральный вид основания и совместить точку D с плоскостью ABС (вращением вокруг проецирующих осей). A(20,10,0); B(90,0,10); C(70,40,30); S(60,20,50); D(30,50,20).
Задача 4 Найти точки встречи прямой АВ с поверхностью
конуса (диаметр основания конуса 100). A(145,110,30); B(15,40,122); О(90,60,10); S(90,60,130).
Задача 5 Построить линию пересечения фигуры с
плоскостью и дать полную развертку одной из ее частей.
Р2
Р1
Задача 6 Построить линии пересечения поверхностей.
85
|
Вариант 53 |
|
|
|
Задача 1 |
|
|
Дано: |
прямая MN и одна проекция точек А и К. |
|
|
Построить: |
параллелограмм ABCD с большей стороной ВС на прямой MN, исходя из условия, что точка К, осно- |
||
вание высоты, делит ее в отношении 1:2 от точки В к точке С и угол В равен 60°. Определить углы наклона высоты к |
|||
плоскостям проекций П1 и П2. M(180,25,10); N(30,90,10); А(170,-,60), К(140,-,10). |
|
||
|
Задача 2 |
|
|
Дано: |
плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK.. |
||
Построить: |
линию пересечения плоскостей. A(195,45,95); B(45,45,90); C(155,125,25), D(140,140,10), |
||
E(205,110,55), F(70,20,100). |
|
|
|
|
Задача 3 |
|
Задача 5 |
Дано: |
пирамида ABCS и точка D. |
Построить линию пересечения фигуры с плос- |
|
Определить: |
высоту пирамиды и угол между гранью |
костью и дать полную развертку одной из ее частей. |
|
SAB и основанием АВС (способом замены плоскостей про- |
|
|
|
екций). Определить натуральный вид основания и совмес- |
|
|
|
тить точку D с плоскостью AСS (вращением вокруг про- |
|
С2 |
|
ецирующих |
осей). A(80,30,20); B(0,10,10); C(30,0,50); |
|
|
S(40,40,30); D(90,10,30). |
|
|
|
|
Задача 4 |
|
|
Найти точки встречи прямой АВ с поверхностью конуса |
А2 |
В2 |
|
(диаметр основания конуса 100). A(35,50,108); |
|||
B(155,115,22); О(90,60,10); S(90,60,130). |
|
|
|
|
|
А1 |
В1 |
|
|
|
|
|
|
|
С1 |
|
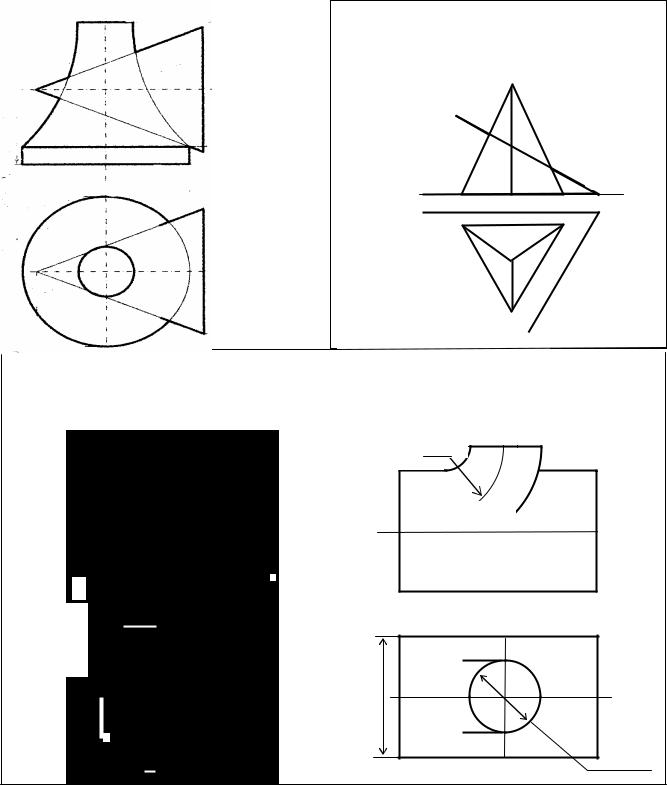
Задача 6 |
|
|
|
Построить линии пересечения поверхностей. |
|
|
|
|
|
90 |
|
|
R65 |
|
|
|
R65 |
|
|
|
|
75 |
|
|
80 |
|
|
|
|
60 |
|
86 |
|
|
Вариант 54
Задача 1 Дано: прямая MN и одна проекция точек А и К.
Построить: параллелограмм ABCD с большей стороной ВС на прямой MN, исходя из условия, что точка К, основание высоты, делит ее в отношении 1:2 от точки В к точке С и угол В равен 60°. Определить углы наклона высоты к плоскостям проекций П1 и П2. M(200,90,10); N(30,30,10); А(30,-,50), К(60,-,10).
Задача 2
Дано: плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK..
Построить: линию пересечения плоскостей. A(180,120,120), B(5,105,55), C(145,0,0), D(210,70,0), E(125,105,70), F(0,45,105).
Задача 3
Дано: пирамида ABCS и точка D. Определить: высоту пирамиды и угол между гранью SAB и основанием АВС (способом замены плоскостей проекций). Определить натуральный вид основания и совместить точку D с плоскостью AСB (вращением вокруг проецирующих осей). A(0,15,10); B(70,10,20); C(50,40,30); S(30,20,50); D(75,35,20).
Задача 4 Найти точки встречи прямой АВ с поверхностью ко-
нуса (диаметр основания конуса 100). A(140,100,35); B(25,40,125); О(90,60,10); S(90,60,130).
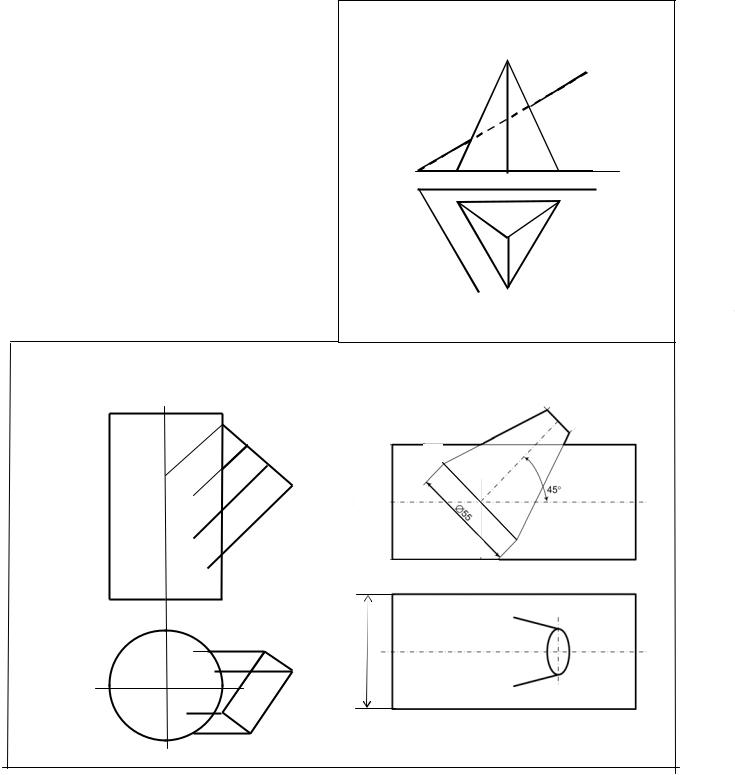
Задача 5 Построить линию пересечения фигуры с плос-
костью и дать полную развертку одной из ее частей.
С2
|
|
|
В2 |
А2 |
|||
|
|
|
|
А1 |
В1 |
|
С1
Задача 6 Построить линии пересечения поверхностей.
Ø80
87
Вариант 55
Задача 1
Дано: прямая MN, точка А.
Построить: равнобедренную трапецию ABCD с большим основанием на прямой MN, исходя из условия, что острый угол равен 60° и меньшее основание равно боковой стороне. Определить углы наклона высоты к плоскостям про-
екций П1 и П2. M(200,160,100); N(10,70,100); А(80,40,40).
Задача 2
Дано: плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK..
Построить: линию пересечения плоскостей. A(185,120,120); B(5,55,105); C(160,0,0), D(210,0,70), E(85,35,5), F(0,100,45).
Задача 3
Дано: пирамида ABCS и точка D. Определить: высоту пирамиды и угол между гранью SAB и основанием АВС (способом замены плоскостей проекций). Определить натуральный вид основания и совместить точку D с плоскостью AСS (вращением во-
круг проецирующих осей). A(80,30,30); B(0,20,0); C(20,0,50); S(30,50,30); D(90,0,30).
Задача 4 Найти точки встречи прямой АВ с поверхностью конуса
(диаметр основания конуса 100). A(30,45,120); B(160,110,20); О(90,60,10); S(90,60,130).
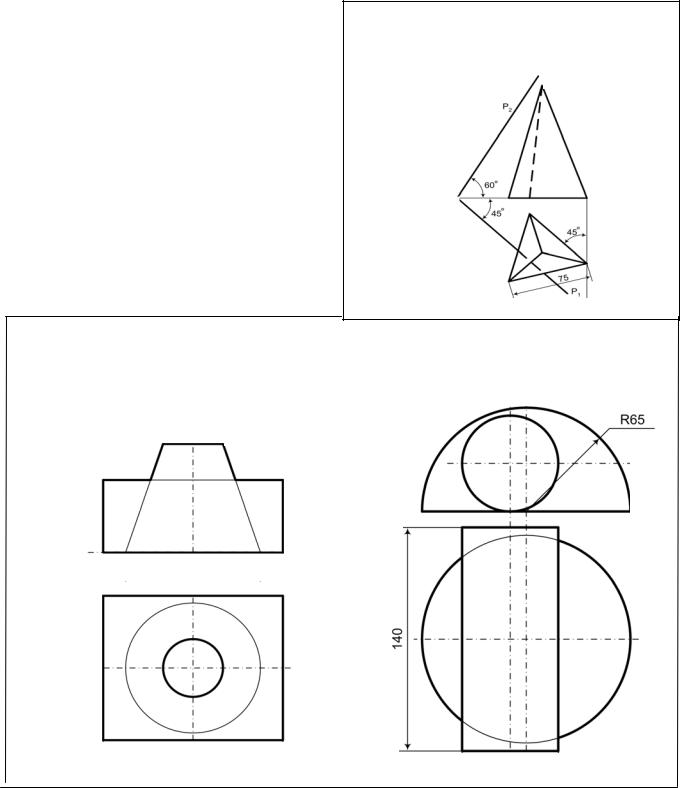
Задача 5 Построить линию пересечения фигуры с плос-
костью и дать полную развертку одной из ее частей.
Задача 6 Построить линии пересечения поверхностей.
88
Вариант 56
Задача 1
Дано: прямая MN, точка А.
Построить: равнобедренную трапецию ABCD с большим основанием на прямой MN, исходя из условия, что острый угол равен 60° и меньшее основание равно боковой стороне. Определить углы наклона высоты к плоскостям про-
екций П1 и П2. M(210,30,100); N(10,130,100); А(130,10,50).
|
Задача 2 |
|||||||||||
Дано: |
плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK.. |
|||||||||||
Построить: |
линию пересечения плоскостей. A(185,140,115); B(0,30,45); C(105,0,15), D(165,115,0), E(215,55,30), |
|||||||||||
F(65,25,115). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3 |
|
|
|
|
|
|
|
|
|
|
|
|
Задача 5 |
|||||||||||
Дано: |
пирамида ABCS и точка D. |
|||||||||||
Определить: |
высоту пирамиды и угол между гранью |
Построить линию пересечения фигуры с плос- |
||||||||||
SAB и основанием АВС (способом замены плоскостей |
костью и дать полную развертку одной из ее частей. |
|||||||||||
проекций). Определить натуральный вид основания и |
|
|
|
|
|
|
|
|
|
|
|
|
совместить точку D с плоскостью ABC (вращением во- |
|
|
|
|
|
|
||||||
|
|
Р2 |
||||||||||
|
|
|
|
|
|
|
||||||
круг проецирующих осей). A(80,0,10); B(10,10,0); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
C(60,40,30); S(50,20,50); D(95,20,15). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4 |
|
|
|
|
|
|
|
|
|
|
|
Найти точки встречи прямой АВ с поверхностью конуса |
|
|
|
|
|
|
|
|
|
|
|
|
(диаметр основания конуса 100). A(145,115,45); |
|
|
|
|
|
|
|
|
|
|
|
|
B(35,15,115); О(90,10,60); S(90,130,60). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Р1
Р1
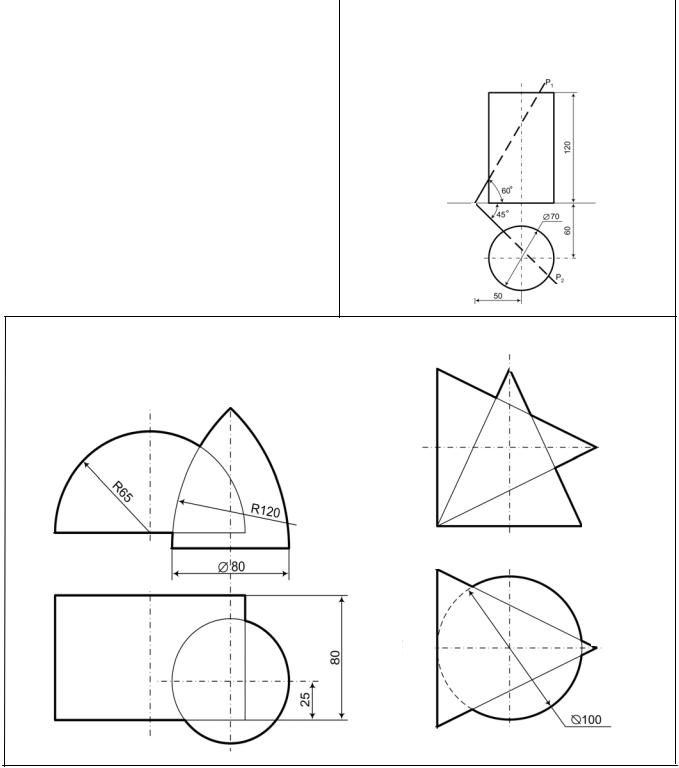
Задача 6 Построить линии пересечения поверхностей.
89
Вариант 57
Задача 1
Дано: прямая MN, точка А.
Построить: равнобедренную трапецию ABCD с большим основанием на прямой MN, исходя из условия, что острый угол равен 60° и меньшее основание равно боковой стороне. Определить углы наклона высоты к плоскостям про-
екций П1 и П2. M(200,90,30); N(20,90,150); А(110,30,20).
Задача 2
Дано: плоскость А, заданная треугольником АВС, и плоскость В, заданная параллелограммом DEFK..
Построить: линию пересечения плоскостей. A(185,112,145); B(0,45,30); C(105,15,0), D(215,28,58), E(160,0,115), F(15,85,85).
Задача 3
Дано: пирамида ABCS и точка D. Определить: высоту пирамиды и угол между гранью SAB и основанием АВС (способом замены плоскостей проекций). Определить натуральный вид основания и совместить точку D с плоскостью ACS (вращением во-
круг проецирующих осей). A(10,25,20); B(90,15,10); C(70,0,50); S(60,40,20); D(20,40,40).
Задача 4 Найти точки встречи прямой АВ с поверхностью конуса
(диаметр основания конуса 100). A(25,5,105); B(170,140,30); О(90,10,60); S(90,130,60).
Задача 5 Построить линию пересечения фигуры с плос-
костью и дать полную развертку одной из ее частей.
В2
С2
А2 D2
А1 В1
D1 |
С1 |
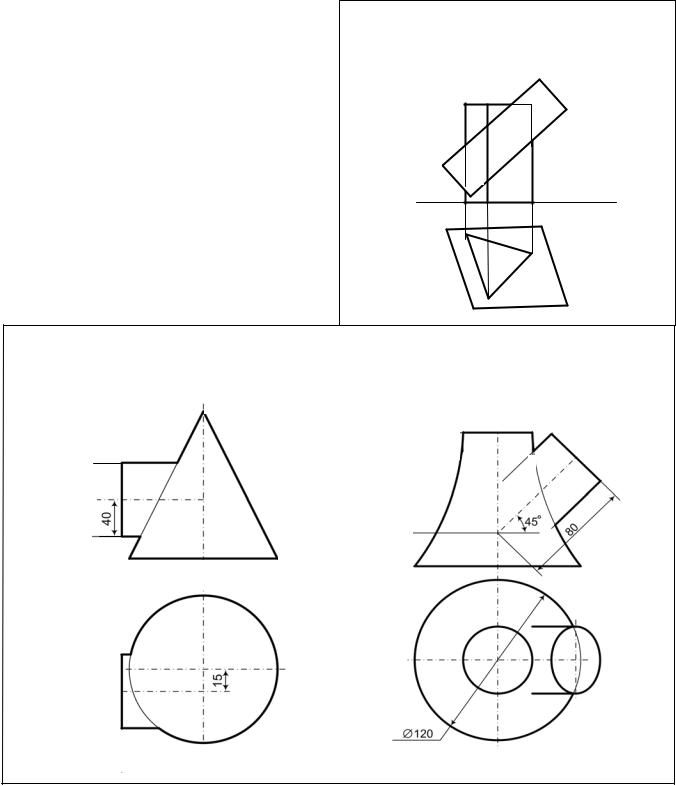
Задача 6 Построить линии пересечения поверхностей.
Ø50
90
