
-resource-254-29254-files-samiit271
.pdfМинистерство путей сообщения РФ Департамент кадров и учебных заведений Самарская государственная академия путей сообщения
Кафедра « Инженерная графика»
Задания
для индивидуальных работ по НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ для студентов 1 курса всех специальностей очной и заочной форм обучения
Составители: Антипов В.А. Изранова Г.В.
Самара 2003
УДК 744
Методические указания и задания для индивидуальных работ по НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ для студентов 1 курса очной и заочной форм обучения.- Самара: СамГАПС, 2003. – 96 c.
Утверждено на заседании кафедры 19 ноября 2003 г., протокол № 4
Печатается по решению редакционно-издательского совета академии.
Методические указания и задания для индивидуальных работ по НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ предназначены для студентов 1 курса всех специальностей.
Составители: Антипов В.А. Изранова Г.В.
Рецензенты: Морогов В.М. – доктор техн. наук, профессор кафедры «Строительноые, дорожные машины и технология машиностроения»; Зиновьева Т.Ю. – канд. техн. наук, доцент кафедры «Инженерная графика»
Редактор: |
Шимина И.А. |
Подписано в печать 15.12.03 Формат 60х80 1/16 Бумага офсетная. Печать оперативная. Усл.п.л. 6,0 Тираж 100 экз. Заказ № 186.
©Самарская государственная академия путей сообщения, 2003.
2
1.ОБЩИЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Решение задач (варианты с 1 по 30): задачи №1…7, а также (варианты с №31 по №61): задачи №1,2,4 следует выполнять на миллиметровке, бумаге в клетку или ватмане. Размер листов должен соответствовать стандарту формата А4 (210х297 мм). На формате выполняется рамка (слева 20 мм, с остальных сторон по 5 мм). В верхней части формата выполняется «Шапка», в которой чертежным шрифтом (номер 7) карандашом отражается следующая информация: фамилия и инициалы студента, номер учебной группы (или шифр студента З/о), номер варианта (например, «Вариант 7»), номер задачи (например, задача 2).
Ниже ручкой (разборчиво!) с разлиновкой строк излагается условие задачи.
Еще ниже дается графическое решение задачи в тонких линиях, в карандаше. После выполнения решения в карандаше исходные данные задачи выделяются зеленой пастой или фломастером, а итог решения –красной пастой или фломастером.
Далее следует поэтапное решение задачи, ручкой, разборчивым почерком, с разлиновкой строк.
Поэтапное описание включает формулировку использованных при решении теорем и укрупненное описание построений. Например, используя теорему о перпендикулярности прямой к плоскости (прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым лежащим в этой плоскости) восстанавливаем в точке А перпендикуляр к плоскости (а ║ в)….
Алгоритмическое описание типа: строим а ┴ в, вводим т. К э а и т.п. не допускается. Допускается при недостатке места выполнять описание решения на обратной стороне
формата.
Решение задач (варианты с №1 по №30) №8 и 9, а также задач 3,5,6 (варианты с №31 по №61)выполняется на ватмане форматом А3 (297 х 420) на с заполнением всех граф (включая графу 26) основной надписи. Эти задания называют эпюры.
На листе выполняется рамка и основная надпись по ГОСТ 2.104-68. Толщины линий на эпюрах выполняются в соответствии с ГОСТ 2.303-68. При этом линии видимого контура рекомендуются выполнять толщиной 0,8… 1 мм, линии невидимого контура, осевые линии и штриховка 0,4 –0,5 мм, вспомогательные линии –0,2…0,3 мм (эти линии после выполнения решения не убирать!)
В графе 2 основной надписи шрифтом № 7 дается информация:
ГРИГ 02.014.05, где ГРИГ означает: графическая работа по инженерной графике, 02означает номер графического задания в семестре, 014 – номер варианта, 05 – номер задачи.
Вграфе 9 основной надписи (организация-исполнитель) шрифтом номер 5 дается информация типа: СамГАПС гр.321 (или шифр студента з/о)
Вграфе 26 (14х70) перевернутая надпись графы 2.
Вграфе №1 шрифтом номер 7 выполняется надпись типа: ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
Вграфе№3 шрифтом №7 –надпись «Эпюр №1».
Вграфах 11 и 12 –фамилия и надпись лиц, выполнивших документ и проверяющих документ.
Исходные данные к эпюрам и описание построений выполняются с обратной стороны формата, разборчивым почерком, с разлиновкой строк.
Работа считается законченной, если задача решена правильно и студент бегло комментирует ход решения задачи по просьбе преподавателя.
3
2. ЗАДАНИЯ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ |
|||
|
Вариант 1 |
|
|
Задача 1 |
|
|
Задача 2 |
Через точку К провести прямые, параллельные |
Даны горизонтально-проецирующая прямая АВ |
||
линиям наибольшего наклона плоскости треугольника |
и линия общего положения CD. Пересечь эти прямые |
||
к плоскостям проекций П1 и П2. |
|
третьей прямой линией, перпендикулярной им, и оп- |
|
|
|
ределить кратчайшее расстояние между скрещиваю- |
|
В2 |
|
щимися прямыми АВ и CD. |
|
|
|
|
|
|
С2 |
|
|
|
|
В2 |
С2 |
А2 |
|
А2 |
D2 |
|
|
|
|
|
С1 |
|
D1 |
А1 |
|
А1=В1 |
|
|
|
C1 |
|
|
|
|
|
В1 |
|
|
|
Задача 3 |
|
|
Задача 4 |
Способом замены плоскостей проекций преоб- |
Вращением вокруг линии уровня найти нату- |
||
разовать заданную плоскость так, чтобы она стала го- |
ральную величину треугольника DEF. |
||
ризонтально-проецирующей. |
|
|
|
F2 |
|
|
F2 |
D2 |
|
D2 |
|
|
E2 |
|
E2 |
|
E1 |
|
E1 |
D1 |
|
D1 |
|
F1 |
|
|
|
Задача 5 |
|
|
Задача 6 |
Построить линию пересечения плоскостей. |
Найти точки встречи прямой с многогранни- |
||
|
|
ком. |
|
b2 |
Z2 |
b2 |
|
|
|
||
a2 |
|
|
|
b1 |
|
|
|
a1 |
|
|
|
Z1 |
|
|
|
|
|
b1 |
|
|
|
4 |
|
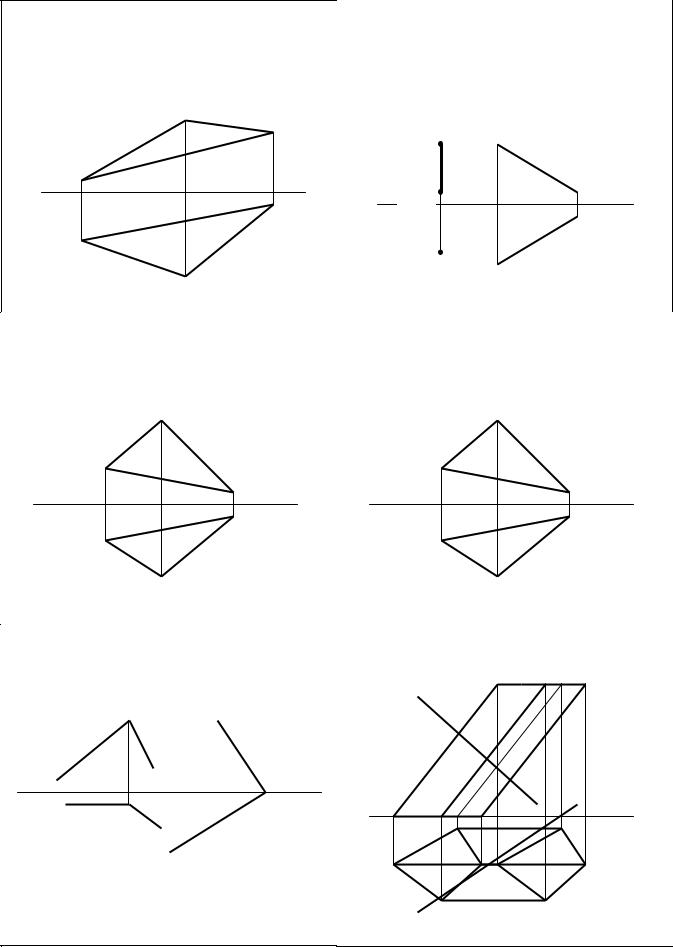
Задача 7 |
Задача 8 |
Построить проекции и истинную величину се- |
Построить проекции и истинную величину фи- |
чения тела плоскостью. |
гуры сечения тела плоскостью Р. Построить развертку |
|
с нанесением на ней линий сечения. |
Р2 |
|
|
Р2 |
Х |
|
Р1 |
Х |
Рх |
|
|
Р1 |
Задача 9 |
|
Построить линии пересечения поверхностей |
|
5
|
Вариант 2 |
|
|
|
Задача 1 |
|
|
Задача 2 |
|
Определить углы наклона отрезков прямых |
Даны точка А и горизонтальная прямая MN. |
|||
EFи МК к П1 и П2. |
|
Построить равнокатетный прямоугольный тре- |
||
|
|
угольник АВС, катет ВС которого лежит на прямой |
||
F2 |
|
MN. |
|
|
|
|
|
|
|
E2 |
M2 |
|
|
|
|
|
|
N2 |
|
|
|
|
А2 |
|
N2 |
|
М2 |
|
|
|
|
|
|
|
|
|
|
|
пП |
N1 |
M1 |
|
А1 |
N1 |
E1 |
|
|
||
|
|
|
|
|
|
|
М1 |
|
|
F1 |
|
|
|
|
Задача 3 |
|
|
Задача 4 |
|
Методом замены плоскостей проекций сде- |
Вращением вокруг линий уровня найти на- |
|||
лать данную плоскость горизонтальной. |
|
туральную величину параллелограмма ABCD. |
||
С2 |
|
|
|
В2 |
|
|
|
|
|
|
|
|
|
А2 |
|
|
С2 |
D2 |
|
А2 |
В2 |
|
|
|
|
|
|
||
|
|
|
В1 |
А1 |
А1 |
|
|
|
|
|
В1 |
|
|
|
С1 |
|
С1 |
D1 |
|
Задача 5 |
|
|
Задача 6 |
|
Построить линии пересечения плоскостей. |
Найти точки встречи прямой с поверхно- |
|||
|
|
стью. |
|
|
О2 |
|
|
|
|
Р2 |
|
а2 |
|
|
|
|
|
|
|
Р1 |
О1 |
|
|
|
|
|
|
|
|
|
|
а1 |
|
|
|
|
6 |
|
|
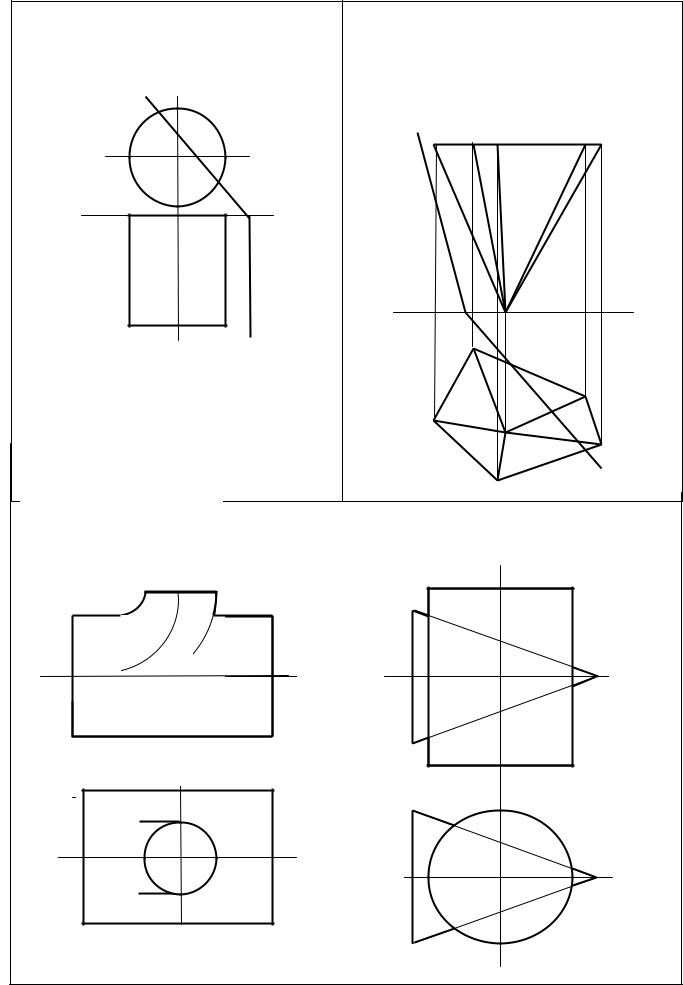
Задача 7 |
Задача 8 |
Построить истинную величину сечения тела |
Построить проекции и истинную величину |
плоскостью. |
фигуры сечения тела плоскостью Р. Построить раз- |
|
вертку с нанесением на нее линий сечения. |
Е2 |
|
|
Р2 |
Е1 |
|
|
Р1 |
Задача 9 |
|
Построить линии пересечения поверхностей. |
|
7
3 вариант |
|
||
Задача 1 |
Задача 2 |
|
|
Определить углы наклона плоскости треуголь- |
Даны точка А и фронтальная прямая MN. По- |
||
ника DEF к П1 и П2 при помощи линии наибольшего |
строить квадрат ABCD, сторона ВС которого лежит на |
||
наклона. |
прямой MN. |
|
|
F2 |
А2 |
С2 |
|
М2 |
|||
|
|
||
D2 |
|
|
|
E2 |
|
|
|
E1 |
М1 |
|
|
D1 |
С |
||
А1 |
|||
|
|
||
F1 |
|
|
|
Задача 3 |
Задача 4 |
|
|
Методом замены плоскостей проекций преоб- |
Методом вращения преобразовать чертеж так, |
||
разовать треугольник АВС так, чтобы превратить его: |
чтобы плоскость, заданная параллельными прямыми |
||
а) в горизонтально-проецирующую плоскость; б) во |
стала горизонтально-проецирующей. |
|
|
фронтально-проецирующую плоскость. |
|
|
|
|
b2 |
|
|
В2 |
a2 |
|
|
|
|
||
С2 |
|
|
|
А2 |
|
|
|
С1 |
a1 |
|
|
|
|
||
А1 |
b1 |
|
|
|
|
||
В1 |
|
|
|
Задача 5 |
Задача 6 |
|
|
Построить линию пересечения плоскостей. |
Найти точки встречи прямой с поверхностью. |
||
С2 |
|
|
|
m2 |
С2 |
|
|
В2 |
|
|
|
n2 |
|
|
|
А2 |
|
|
|
B1 |
|
|
|
n1 |
|
|
|
A1 |
|
|
|
m1 |
|
|
|
С1 |
С1 |
|
|
|
|
||
|
8 |
|
|
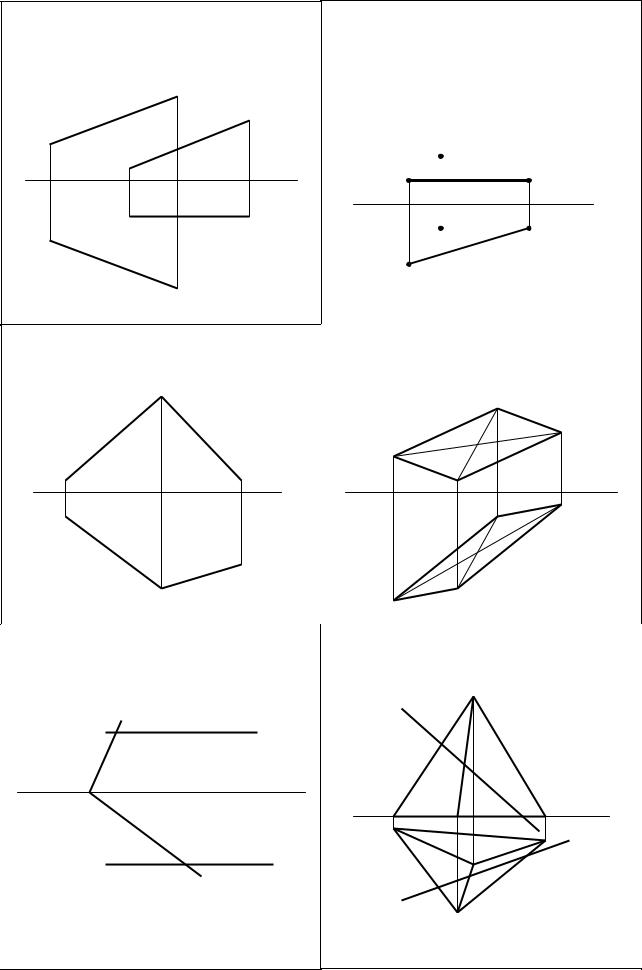
Задача 7 |
Задача 8 |
Найти истинную величину сечения тела плоско- |
Построить линию пересечения многогранника |
стью. |
плоскостью «Р» и дать полную развертку одной из его |
|
частей в соответствии с условиями задачи: |
|
Р2 |
Р1 |
|
|
Р1 |
|
Задача 9 |
Построить линии пересечения поверхностей. |
|
9

|
|
|
|
Вариант 4 |
|
|
|
|
Задача 1 |
|
|
|
|
Задача 2 |
|
Через точку А провести плоскость, перпенди- |
Построить прямоугольный треугольник АВС с |
||||||
кулярную к плоскости EFG (EG – горизонталь, EF – |
катетом ВС на прямой MN исходя из условия, что |
||||||
фронталь). |
|
|
|
|
длина его гипотенузы в 1.5 раза больше высоты. |
||
A2 |
F2 |
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
M2 |
E2 |
|
|
G2 |
|
N2 |
|
|
|
|
|
|
|
|
|
|
E1 |
F1 |
|
|
|
|
|
|
|
|
|
|
N1 |
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
G1 |
|
|
A1 |
M1 |
|
|
|
|
|
|||
|
Задача 3 |
|
|
|
|
Задача 4 |
|
Определить натуральную величину двугранно- |
Вращением вокруг линий уровня найти нату- |
||||||
го угла. |
|
|
|
|
ральную величину параллелограмма ABCD. |
||
|
|
В2 |
|
|
|
|
|
|
|
|
|
|
|
B2 |
|
D2 |
|
|
|
A2 |
A2 |
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
D2 |
|
|
С2 |
|
|
|
A1 |
B1 |
|
D1 |
|
|
B1 |
|
|
||
|
|
|
|
|
|
||
|
|
|
|
A1 |
|
D1 |
C1 |
|
C1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
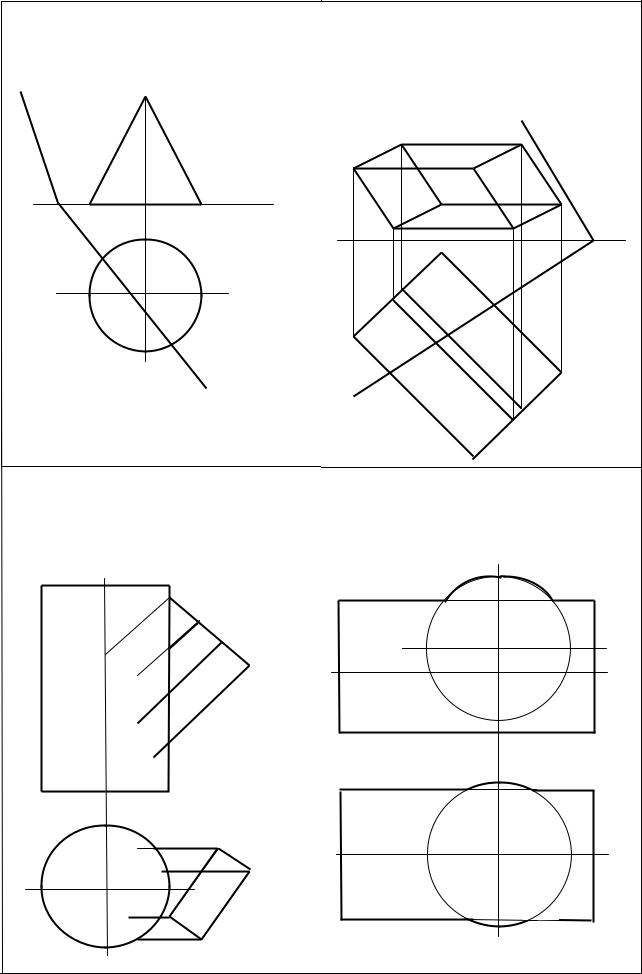
Задача 5 |
|
|
|
|
Задача 6 |
|
Построить линию пересечения двух треуголь- |
Найти точки встречи прямой с плоскостью. |
||||||
ников. Отметить видимость. |
|
|
|
|
|
|
|
|
B2 |
E2 |
|
|
a2 |
|
|
|
|
|
|
|
|
||
A2 |
|
|
|
|
|
|
|
|
|
|
|
F2 |
|
|
|
D2 |
|
E1 |
C2 |
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
С1 |
F1 |
|
|
|
D1 |
В1 |
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
