5.4.4. Оценки качества переходного процесса по вещественной частотной характеристике

Такие оценки оказываются особенно удобными в случае, когда для исследования системы применяются частотные методы, а переходный процесс вызван скачкообразным входным воздействием.

На основании анализа соотношения (5.31) были получены следующие оценки качества переходного процесса.

• Оценка 1. Начальное значение переходной характеристики соответствует конечному значению ВЧХ.

  обычно h(0)=0.

• Оценка 2. Конечное значение переходной характеристики равно начальному значению ВЧХ.

  , обычно h()=k.

  

  Риc. 5.12. Иллюстрация 1-ой и 2-ой оценок

• Оценка 3. Если для частотных характеристик двух систем справедливо выражение

  или ,

  то аналогичное соотношение будет связывать и переходные характеристики:

  (t) = m (t) или (t) = (t) .

  

  Рис. 5.13. Иллюстрация 3-ей оценки

• Оценка 4. В случае, когда частотные характеристики двух систем связаны соотношением

  ,

  для переходных характеристик справедливо равенство

  .

  

  Рис. 5.14. Иллюстрация 4-ой оценки

• Оценка 5. Если R() является положительной невозрастающей функцией, то перерегулирование в системе не будет превышать 18%.

• Оценка 6. Переходная характеристика имеет монотонный характер, если представляет собой отрицательную, убывающую по модулю непрерывную функцию.

• Оценка 7. В случае, когда R() есть локально возрастающая функция, перерегулирование можно оценить по формуле:

  .

  Рис. 5.15. Иллюстрация 7-ой оценки

• Оценка 8. Если на какой-то частоте R() терпит разрыв, то переходная характеристика будет иметь незатухающие колебания этой частоты.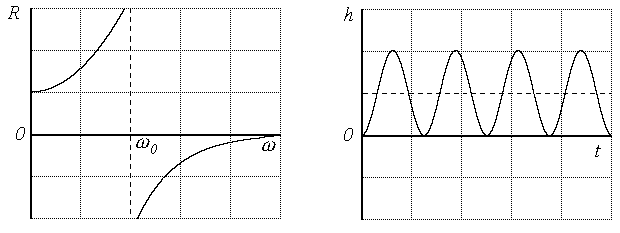

  

  Рис. 5.16. Иллюстрация 8-ой оценки

• Оценка 9. Для монотонных процессов время переходного процесса можно приближенно оценить по формуле:

.

Если частотная характеристика R() всегда положительна, то в качестве выбирается частота, на которой .

Рис. 5.17. Иллюстрация 9-ой оценки Рис. 5.18. Определение частоты

Таким образом, с помощью приведенных оценок можно приближенно (без вычислений) оценить качество переходного процесса по виду вещественной частотной характеристики.

Подробно частотные оценки переходного процесса описаны в работах В.В. Солодовникова.

5.4.5. О начальном участке переходной характеристики

Используя частотный метод, можно оценить не только начальное значение переходного процесса, но и его вид на начальном участке.

Рассмотрим систему с передаточной функцией общего вида:

.

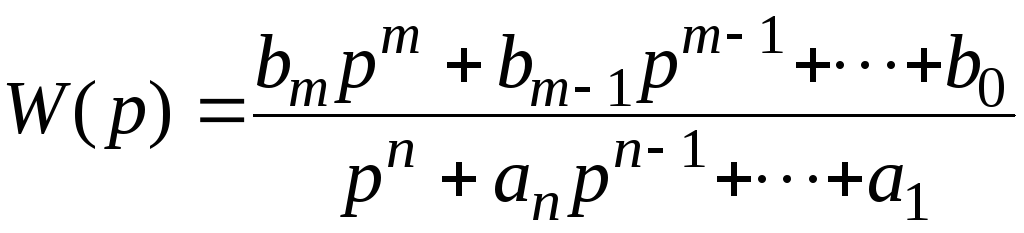Заменив p на j, перейдем к ее частотной характеристике

. (5.32)

Известно, что начальное значение переходного процесса определяет конец частотной характеристики, поэтому в (5.32) устремим . При этом доминирующими слагаемыми в числителе и знаменателе будут в старшей степени, и (5.32) вырождается в

. (5.33)

Частотную характеристику (5.33) имеет интегратор (n-m) порядка, следовательно, и начальный участок переходного процесса соответствует интегратору (n-m) порядка.

В случае, когда передаточная функция системы n-го порядка содержит в числителе просто коэффициент, начальный участок переходного процесса соответствует кривой n-го порядка.