73

УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ

4. Устойчивость линейных непрерывных систем

4.1. Основные понятия и определения

Устойчивость - это основное качественное свойство системы автоматического управления, без которого она неработоспособна. Физически устойчивость означает, что процессы в системе стремятся к определенной величине при любых начальных условиях.

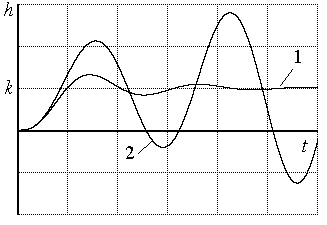
На рис. 4.1. приведены переходные характеристики неустойчивой и устойчивой системы. Для последней справедливо условие

1 - сходящийся процесс, система устойчива.

2 - расходящийся процесс, система неустойчива.

Рис. 4.1. Переходные характеристики системы

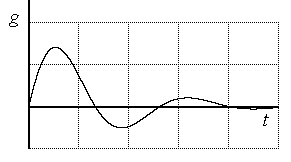
Об устойчивости можно судить также по импульсным переходным функциям (рис. 4.2), которые для устойчивой системы удовлетворяют условию

В случае линейных САУ устойчивость определяется только ее структурой и параметрами и не зависит от внешних воздействий. Рассмотрим, как оценить это свойство для систем типа:

Рис. 4.2. Импульсная переходная функция

(4.1)

Переходные процессы в ней определяются как решение матричного уравнения состояния следующим образом:

(4.2)

Здесь первое слагаемое соответствует свободной составляющей движения, второе - вынужденной.

Основным режимом работы системы является равновесный (статический) режим, при котором переменные состояния с течением времени не меняются, а все производные координат состояния равны нулю.

Покажем, что процесс движения к равновесию можно считать свободным. Предварительно запишем уравнение равновесия, полагая в (4.1)

(4.3)

откуда при det A 0 определим равновесное значение переменных состояния

(4.4)

Введем новые координаты, равные отклонениям от точки равновесия,

(4.5)

и запишем уравнение в отклонениях:

так как (4.6)

После подстановки в (4.6) вместо его значения из (4.1) с учетом (4.5) получим

Окончательно уравнение в отклонениях имеет вид:

(4.7)

Определение. Линейная система называется устойчивой, если для ее процессов выполняется свойство:

. (4.8)

Вид процессов системы (4.7) определяется ее решением, которое находится через матричную экспоненту в виде

(4.9)

Поскольку выражение (4.9) соответствует первой составляющей решения (4.2), то устойчивость линейной системы (4.1) определяется только свойствами автономной системы и не зависит от внешних воздействий. Это означает, что можно не переходить к уравнениям в отклонениях от состояния равновесия, а для анализа устойчивости исследовать свойства матрицы A.

4.2. Условие устойчивости линейных систем

Утверждение. Для устойчивости линейной системы необходимо и достаточно, чтобы вещественная часть всех собственных значений матрицы A (корней характеристического уравнения) была отрицательной.

Re () < 0, (4.10)

Для доказательства найдем корни характеристического уравнения системы (4.1) по выражению

A(p) = det(pI-A) = (4.11)

и используем модальное представление процессов

(4.12)

Как видим, полный процесс представляет собой сумму экспонент, а качественный характер переходных процессов полностью определяется значениями корней .

Если все корни характеристического уравнения вещественные, то в выражении имеем обычные экспоненты. При выполнении условия (4.10) они носят затухающий характер, следовательно, и их сумма также будет с течением времени стремиться к нулю (рис. 4.3).

Рис. 4.3. Процессы в системе с вещественными корнями

В случае, когда корни характеристического уравнения комплексные, для каждой пары получим колебательную составляющую, которая мажорируется

затухающей экспонентой при отрицательной вещественной части данной пары корней. Следовательно, и процесс, определяемый соотношением (4.12), будет затухающим при выполнении условия (4.10).

Таким образом, мы доказали достаточность условия устойчивости (4.10).

Рис. 4.4. Процессы в системе с комплексными

корнями и отрицательной вещественной частью

Необходимость этого условия докажем способом “от противного”.

Предполагаем, что хотя бы один из корней имеет положительную вещественную часть. Тогда соответствующая экспонента будет с течением времени стремиться к бесконечности. Следовательно, полный процесс, определяемый выражением (4.12), будет иметь расходящийся характер, а система (4.1) никогда не сможет стать устойчивой.

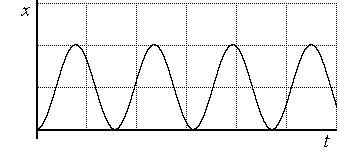
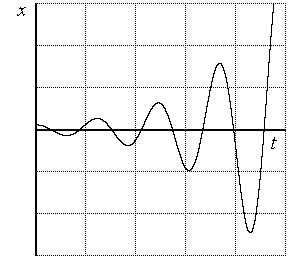
Рис. 4.6. Процессы в системе с чисто

мнимыми корнями

Рис. 4.5. Процессы в системе с положительной

вещественной частью корней

Корни характеристического уравнения (4.11) можно представить на комплексной плоскости в виде точек (рис. 4.7). При этом получим графическую интерпретацию условия (4.10): для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения располагались в левой полуплоскости плоскости корней.

Если хотя бы один корень находится в правой полуплоскости плоскости корней, то система будет неустойчива. Мнимая ось представляет собой границу устойчивости системы, то есть при наличии хотя бы одного корня на этой оси система находится на границе устойчивости (при условии. что все остальные корни имеют отрицательную вещественную часть).

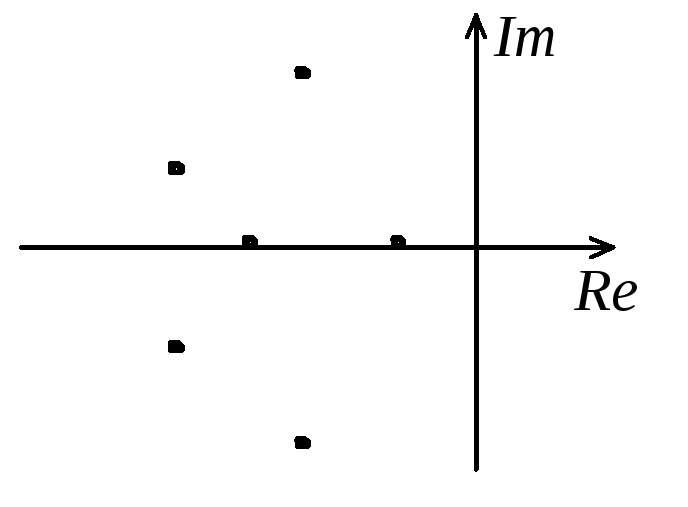
Рис. 4.7. Распределение корней устойчивой системы

Необходимым (но не достаточным) условием устойчивости является положительность всех коэффициентов характеристического уравнения. В этом нетрудно убедиться, если представить характеристический полином A(p) в виде произведения

Если корни вещественные, то есть и > 0, то характеристическое уравнение принимает вид

Раскрывая скобки, получим уравнение типа (4.11), где все коэффициенты будут положительными. Аналогичный результат получится и в случае, когда корни комплексно-сопряженные с отрицательной вещественной частью.

Таким образом, при положительных коэффициентах характеристического уравнения (4.11) система может быть как устойчивой, так и неустойчивой - необходима дополнительная проверка. При наличии хотя бы одного отрицательного коэффициента она наверняка неустойчива, никаких дополнительных исследований не требуется.