5.4.2. Взаимосвязь между частотной характеристикой и импульсной переходной функцией

Будем рассматривать линейную систему с известной передаточной функцией

W(p) = ,

от которой с помощью замены p на j перейдем к ее частотной характеристике W(j).

Соответствие между импульсной переходной функцией и частотной характеристикой устанавливает обратное преобразование Фурье

. (5.23)

Представим частотную характеристику W(j) следующим образом:

, (5.24)

а экспоненту на основе формулы Эйлера запишем в виде:

. (5.25)

В результате подстановки (5.24) и (5.25) в выражение (5.23) получим

Импульсная переходная функция является вещественной, поэтому в последнем выражении мнимая часть должна быть равна нулю. Это нетрудно показать.

Здесь cost есть четная функция частоты, а sint - нечетная. Вещественная часть R() содержит четные степени частоты, и является четной функцией; мнимая часть, - нечетная. Следовательно, произведения R()sint и I()cost представляют собой нечетные функции, а интегрирование их суммы во всем диапазоне частот дает

.

Таким образом, выражение для импульсной переходной функции принимает вид:

. (5.26)

В (5.26) подынтегральная функция четная, поэтому можно перейти к интегрированию по положительным частотам и удвоить результат, что дает

. (5.27)

Здесь время t является параметром, так как интегрирование осуществляется по. В то же время известно, что импульсная переходная функция при t < 0 отсутствует, то есть g(-t) = 0. Это свойство используем для упрощения выражения (5.27), где в результате замены t на -t получим:

.

Отсюда следует

. (5.28)

После подстановки (5.28) в (5.27) получим два соотношения для импульсной переходной функции:

. (5.29)

. (5.30)

В расчетной практике чаще используется вещественная частотная характеристика и соотношение (5.29).

Обычно для анализа бывает необходима переходная характеристика, поэтому установим ее связь с вещественной частотной характеристикой.

5.4.3. Взаимосвязь между частотной и переходной характеристиками

Поскольку переходная характеристика связана с импульсной переходной функцией соотношением

,

то после подстановки в него (5.37) получим

.

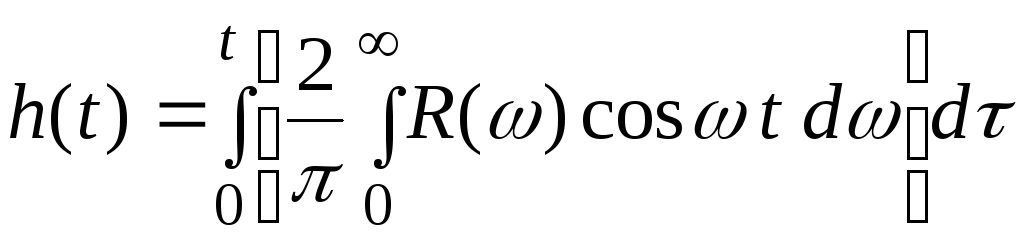Здесь произведение R()cost - функция двух переменных, поэтому изменим порядок интегрирования и запишем

.

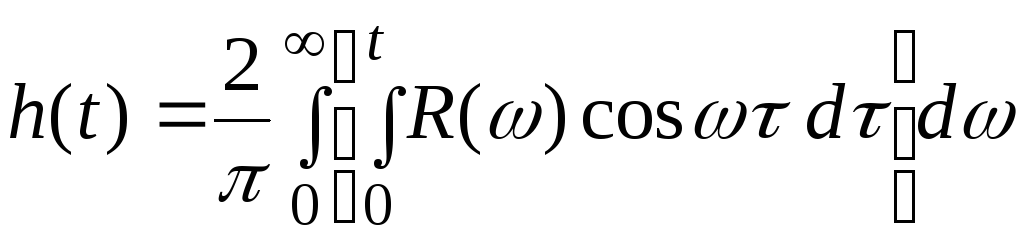В результате получим следующее соотношение, связывающее переходную и вещественную частотную характеристику:

. (5.31)

Типичный вид вещественной частотной характеристики, которая может быть получена экспериментально, представлен на рис. 5.10.

В теории управления были разработаны различные способы вычисления переходной характеристики при аппроксимации R() различными функциями, например, метод трапеций и треугольников.

Риc. 5.11. Вещественная частотная характеристика системы

В настоящее время необходимость в них отпала, так как с помощью средств вычислительной техники можно с достаточной степенью точности построить характеристики h(t).

Однако, выражение (5.31) используется для оценки вида переходного процесса без построения всей кривой h(t).