Дифференциальные уравнения второго порядка

Наиболее важными для практики являются линейные уравнения второго порядка.

Эти уравнения имеют вид

.

Общим решением этого уравнения будет

,

где — общее решение соответствующего уравнения без правой части (однородного):, а— некоторое частное решение исходного уравнения.

Будем рассматривать наиболее часто встречающиеся в практике случаи, когда коэффициенты являются постоянными числами, а правая часть имеет простой (специальный) вид. Для нахождениясоставляется характеристическое уравнение, находятся его корниии, в зависимости от их значений, определяется.

Правило нахождения укажем в таблице № 1:

Характеристическое уравнение: Дискриминант:

1. — действительные и различные:

2.— действительные и равные:

3.— комплексно сопряженные:

Частное решение y^* находится по правилу, указанному в таблице №2:

f(x)	y*
f(x)=Pn(x)	1.y*=Qn(x), если среди корней характеристического уравнения нет числа 0. 2.y*=Qn(x)x, если число 0 является однократным корнем характеристического уравнения. 3.y*=Qn(x)x2, если число 0 является двукратным корнем характеристического уравнения.
f(x)=Pn(x)ex	4.y*=Qn(x)ex, если среди корней характеристического уравнения нет числа . 5.y*=Qn(x) exх, если  является однократным корнем характеристического уравнения. 6.y*=Qn(x)exх2, если  является двукратным корнем характеристического уравнения.
f(x)=a0cosx+b0sinx	7.y*=Aсosx+Bsinx, если число i, где - мнимая единица, не является корнем характеристического уравнения. 8.y*=(Acosx+Bsinx)х, если число i является корнем характеристического уравнения.

В этой таблице Q_n(x)=A₀xⁿ+ A₁x^n-1+…+ A_n многочлен той же степени, что и P_n(x), но с неизвестными коэффициэнтами, которые и нужно найти.

Примеры.

1.Найти общее решение уравнения у^// – 5у^/=х.

Обозначим искомое решение через у. Тогда у=у+у^*, где у — общее решение уравнения у^// – 5у^/=0. Составим характеристическое уравнение: k²-5k=0; k(k-5)=0; k₁=0; k₂=5. Следовательно у=с₁е^0х+с₂е^5х=с₁+с₂е^5х. Найдем теперь у^*. Так как правая часть уравнения равна f(x)=1х+0, то частное решение у^* было бы: у^*=Ах+В, если бы числа 0 не было среди корней характеристического уравнения. Но в нашем случае 0 встречается среди корней характеристического уравнения один раз.Это случай 2, табл. № 2 . Поэтому у^*=(Ах+В)х=Ах²+Вх. Найдем (у^*)^/=2Ах+В; (у^*)^//=2А, подставим эти значения в данное уравнение и потребуем, чтобы оно обратилось в тождество:

2А-5(2Ах+В)1х+0; -10Ах+2А-5В1х+0, откуда

.

Таким образом, и общее решение уравнения будет

.

2. Найти общее решение уравнения у^//+4у^/+13у=2cos4x

Обозначим искомое решение через у. Тогда у=у+у^*, где у — общее решение уравнения у^//+4у^/+13у =0. Составим характеристическое уравнение k²+4k+13=0.Решая это уравнения находим корни: k₁=–2+3i; k₂=–2 –3i. Следовательно у=е^-2х(C₁cos3x+C₂sin3x). Найдем теперь у^*.Т.к. =4i нет среди корней характеристического уравнения ( случай 7 табл.2) , то частное решение у^* подбираем в виде у^*=Acos4x+Bsin4x; (у^*)^/=–4Asin4x+4Bcos4x; (у^*)^//=–16Acos4x–16Bsin4x. Подставляем эти значения в уравнение , приводим подобные слагаемые, получаем: cos4x(16B-3A)+sin4x(-16A-3B)=2cos4x. Приравнивая коэффициэнты при sin 4x и cos 4x находим:

Решая систему получаем

Частное решение имеет вид

Общее решение уравнения

3. Найти частное решение уравнения у^//+4у^/+4у=3е^2х, удовлетворяющее начальным условиям у(0)=1, у^/(0)=2.

Найдем сначала общее решение данного уравнения у=у+у^*.

у^//+4у^/+4у=0; k²+4k+4=0; D=16-16=0; Следовательно,у=с₁е^-2х+с₂е^-2хх. Так как числа =2 нет среди корней характеристического уравнения (случай 4 табл. №2), то частное решение у^* подбираем в таком же виде, как и правая часть у^*=Ае^2х; (у^*)^/=Ае^2х2; (у^*)^//=Ае^2х4. Подставляем эти значения в уравнение 4Ае^2х+42Ае^2х+4Ае^2х=3е^2х; 16Ае^2х=3е^2х; 16А=3; А=. Следовательно, у^*=е^2х. Значит, у=у+у^*= =с₁е^-2х+с₂е^-2хх+3/16е^2х — общее решение данного уравнения. Для нахождения частного решения, удовлетворяющего заданным начальным условиям, найдем ещё

у^/=с₁е^-2х(-2)+с₂(е^-2х(-2)х+е^-2х1)+3/16 е^2х2. Так как у(0)=1 и у^/(0)=2, то получим .

Подставляя эти значения в общее решение, найдем окончательно . Это есть частное решение данного уравнения, удовлетворяющее данным начальным условиям.

Ряды

Рассмотрим бесконечную последовательность действительных чисел а₁, а₂, …,а_n,...

Выражение вида

а₁+ а₂+ а₃+ ... а_n+... (2)

называется числовым рядом.

Рассмотрим S_n= а₁+ а₂+ а₃+ ... а_n – n-ю частичную сумму ряда (2)

Если ,гдеS – действительное число, то это число называется суммой ряда (2) ,а сам этот ряд называется сходящимся. Если же S=∞ или не существует вообще, то ряд суммы не имеет и называется расходящимся.

Для рядов с положительными членами справедливы достаточные признаки сходимости.

Признак сравнения.

Пусть даны два ряда

а₁+ а₂+ а₃+ ... а_n+... (3)

b₁+ b₂+ b₃+ ... b_n+... (4)

причем a_n ≤ b_n (n=1, 2, 3,...). Тогда из сходимости ряда (4) следует сходимость ряда (3). Из расходимости ряда (3) следует расходимость ряда (4).

Предельный признак сравнения: если существует конечный и отличный от нуля предел , то оба ряда (3) и (4) одновременно сходятся или одновременно расходятся.

Признак Даламбера.

Если для ряда (2) существует 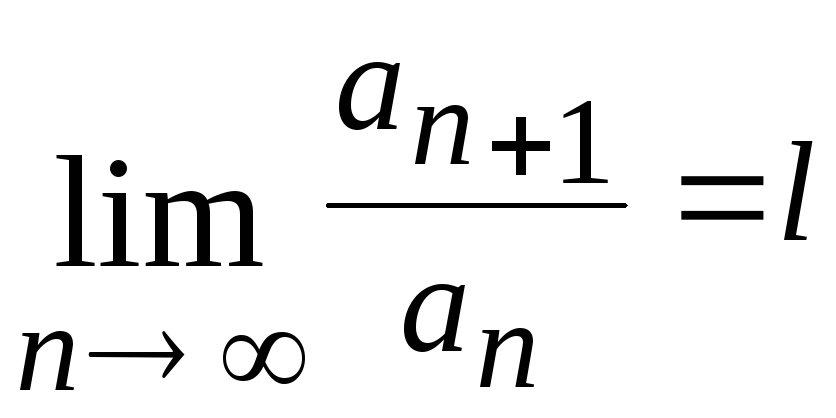, то этот ряд сходится при l<1 и расходится при l>1.

Признак Коши.

Если для ряда (2) существует , то ряд сходится при l<1 и расходится при l>1.

Интегральный признак.

Если f(x) при х≥1 непрерывная, положительная, монотонно убывающая функция, причем f(n)=a_n (n=1,2,...), то ряд (2) сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл .

Для знакочередующихся рядов вида

а₁— а₂+ а₃— ...+...(-1)ⁿ⁺¹а_n+..., (5)

где a_n≥0, справедлив признак Лейбница:

Если абсолютные величины членов ряда (5) монотонно убывают, а общий член ряда стремится к нулю, т.е., если выполняются условия:

1. а₁>а₂> а₃>..> а_n> ... и 2),

то ряд (5) сходится.

Можно доказать, что сумма сходящегося знакочередующегося ряда (5) не превосходит абсолютной величины первого члена этого ряда.

Примеры.

1. Исследовать на сходимость ряд:.

Имеем ,. По признаку Даламбера находим предел:

, т.к. l<1, то ряд сходится.

2. Исследовать на сходимость ряд.

Применим признак Коши. Найдем

.

Следовательно, данный ряд расходится.

3. Исследовать на сходимость ряд .

Сравним этот ряд с рядом

(6)

Имеем, .

Применяя интегральный признак, вычисляем интеграл.

.

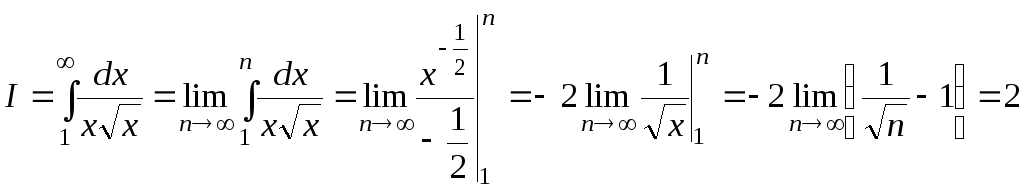Это значит, что интеграл сходится, а, значит, и ряд (6) также сходится. Тогда по признаку сравнения сходится и исходный ряд.

Приложения степенных рядов.

Если функция f (x) имеет производные любого порядка в интервале |х-х₀|< r, где r0, то в этом интервале она может быть разложена в сходящийся ряд Тейлора.

При х₀=0 получается ряд Маклорена:

Приведём разложения в ряды Маклорена и соответствующие области сходимости соответствующих рядов, для наиболее часто встречающихся в практике функций

.

.

.

.

.

Пользуясь разложениями функций в степенные ряды можно вычислять приближенные значения функций в некоторых точках, вычислять определенные интегралы, находить частные решения дифференциальных уравнений.

Пример. Вычислить с точностью до 0,001.

Первообразная для функции не выражается через элементарные функции. Поэтому точное значение интеграла вычислить мы не сможем. Но с помощью рядов Маклорена и действий над ними можно вычислить данный интеграл с любой степенью точности. Для этого воспользуемся известным разложением в ряд:

.

Ряд, стоящий справа равномерно сходится к функции при любом действительномt. Заменим t на . Получим

.

Это разложение также верно при любом действительном х. Проинтегрируем последнее равенство в пределах от 0 до 0,5.

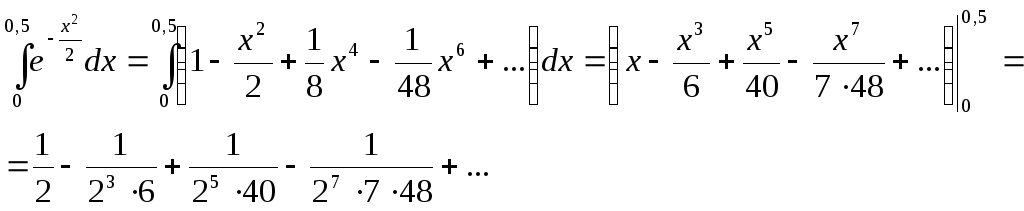
Мы получили знакочередующийся ряд. Известно, что сумма знакочередующегося ряда не превосходит абсолютной величины его первого члена. Поэтому ряд, начинающийся с третьего члена, будет иметь сумму не превосходящую . Таким образом, если мы отбросим в правой части все слагаемые, начиная с третьего, то сделаем ошибку не большую 0,001.

Итак, с точностью до 0,001 имеем: .

Округляя до тысячных долей получим окончательно

.

32