2.3 Определение эффективности загрузки бункера новым способом

При традиционном способе загрузки бункеров сверху с помощью материалопроводов, расположенных вне бункера и разгрузителя, установленного на его крышке, высота подъема материала Н, а значит производительность и время загрузки – величины постоянные [2]. При загрузке бункера снизу с помощью распределительного телескопического материалопровода и рассекателя потока происходит изменение высоты подъема материала (высоты материалопровода) [3]. Определим, как в этом случае будет изменяться время загрузки в процессе заполнения бункера. Для этого найдем вначале изменение высоты подъема материала от времени

, (8)

где G(t) = 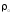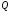(h) – производительность загрузки бункера, а (h) определяется по формуле

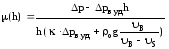, (9)

полученной из выражения

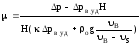(10)

для вычисления массовой расходной концентрации аэросмеси 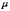при традиционном способе загрузки бункера. При этом выражение (3) является следствием известного соотношения

для вычисления потери давления аэросмеси в вертикальном материалопроводе [2, 5],

гдеудельные гидравлические потери при движении воздушного потока на вертикальном участке материалопроовода высотой 1 м;

 – коэффициент Гастерштадта;

 – массовая расходная концентрация аэросмеси, кг/кг.

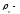плотность стандартного воздуха,кг/м³;

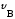–скорость воздушного потока, м/с;

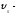скорость витания частиц, м/с.

Дифференцируя (1), получаем

(11)

Подставив (9) в (11), получим

(12)

Далее для сокращения записей положим

, В=, С=.

Тогда (12) перепишется следующим образом

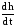=А,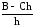

откуда

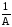
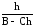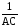
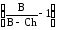dt=dh=dh,

т.е.

dt=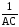dh.

Интегрирую обе части последнего равенства, получим

t =  = =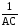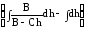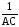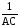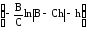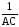 

 = +C₁ = –+C₁,

т.е.

t = –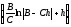+C₁. (13)

Постоянную С₁ найдем из начального условия h(0) = h₀:

0 = –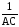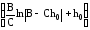+C₁,

откуда

C₁ = .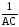

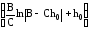Подставляя найденную постоянную С₁ в (6), получим

t = –+,

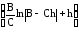откуда

t = 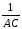. (14)

Полагая в (14) h = H, получим формулу

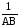
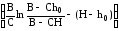= . (15)

для нахождения времени заполнения бункера высотой Н, заполненного в начальный момент до уровня h₀.

Если в начальный момент загрузки бункер был пуст, т.е. h₀ = h(0) = 0, то из (15) вытекает

Т₀ = 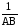 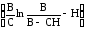(16)

времени заполнения бункера высотой Н

Если положить

D = ,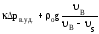

то

,

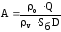откуда и из (16) следует

Т₀ = .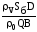

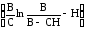Последнюю формулу можно записать более компактно, если ввести новый параметр Е = :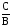

Т₀ =  (17)

Из (9) следует, что 1–ЕН > 0, откуда, учитывая Н > 0, находим область определения функции Т₀(Н):

Н  (0; 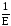) = (0; ).

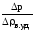Ясно, что время Т₀ загрузки бункера снизу с помощью распределительного телескопического материалопровода меньше времени Т₁ заполнения бункера традиционным способом. Для нахождеия разности Т₁ – Т₀ воспользуемся известной [2, 5] формулой (для упрощения расчетов объем днища бункера не учитывается).

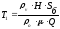, (18)

где – объемная масса материала, кг/м³ ;

–площадь сечения бункера, м² ;

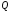–подача (расход) воздуха, м³/с ;

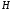–высота материалопровода, м.

Формула (18), используя легко выводимые из (3) соотношения

 = ,

можно преобразовать к виду

Т₁ =  = =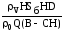

 = =,

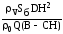т.е.

Т₁ = . (19)

Тогда из (17) и (19) следует

Т₁ – Т₀ = =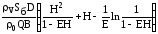

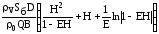 = . (20)

Формулу (20), используя равенство Е = 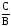 можно записать в другой форме

Т₁ – Т₀ = 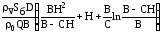. (21)

Так как производная

(Т₁ – Т₀) = ·.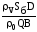

функции (Т₁ – Т₀) (Н) в области её определения

Н  (0; 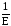) = (0; )

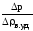всегда положительна, то функция (Т₁ – Т₀) (Н) является возрастающей на интервале (0; ).

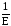Таким образом, время загрузки бункера любой высоты снизу с помощью распределительного телескопического материалопровода всегда меньше времени загрузки этого же бункера традиционным способом сверху. Причём, чем больше высота бункера, тем больше выигрыш во времени, который определяется по формулам (20) или (21).