2. Простейшие разрывные функции

Для расчета характеристик электрических цепей во временной области используются испытательные сигналы. Простейшие разрывные функции, которыми широко пользуются в теории сигналов, моделировании и испытании цепей, представлены в табл. 3.1. Ниже приводится краткое описание этих функций.

1. Функция знака (сигнум-функция) (табл. 3.1, поз 1). Функция имеет постоянную величину, равную единице, знак кото­рой скачком изменяется при переходе переменной t через нуль

Таблица 3.1

№ п/п	Название функции*	Аналитическая запись функции	Графическое изображение	Связь между функциями
1	Функция знака sign(t) (сигнум- функция)	Sign(t)=		_
2	Единичная функ­ция (функция Хе­висайда)	=
3	Дельта-функция (функция Дирака)	=
4	Прямоугольный импульс с единич­ной высотой rect(t/)

*Функции могут иметь и другой аргумент, например частоту .

Умножение произвольной функции f(t)на sign(t) означает изме­нение знака f(t) в момент времени t = 0.

2. Единичная функция или единичный скачок (функция Хеви­сайда) 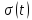(табл. 3.1, поз. 2). Функция определяется:

=

Сопоставляя (3.3) и (3.4), получаем

Умножение сигнала s(t) на единичную функцию равносильно включению этого сигнала в момент t = 0

s(t)

Этим приемом широко пользуются для описания односторонних финитных (ограниченных по времени) сигналов.

3. Дельта-функция или дельта-импульс (функция Дирака) (табл. 3.1, поз. 3). По определению -функция удовлетворяет следующим двум условиям:

=

и

т. е. -функция равна нулю при всех отличных от нуля значениях аргумента, принимая в точке t=0бесконечно большое значение. Площадь -функции равна единице.

Остановимся на некоторых свойствах -функции.

а) (t) является четной функцией аргумента

Из (3.6) следует, что

Тогда

Сопоставляя (3.9) и (3.4), получим

или

Следовательно, используя понятие δ-функции, можно выразить производную от разрывной функции в точке ее разрыва.

б) фильтрующее свойство δ-функции. Это свойство выражает­ся соотношением

прит. е. интеграл от произведения произвольной функ­цииf(t), ограниченной в интервале времени(,), на дельта-функциюравен значению функцииf(t) в точке(рис. 3.2,а).

в) результатом умножения произвольной функции f(t) наявляется дельта-функция, площадь которой равна значению функцииf(t) в точке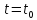(рис. 3.2,б)

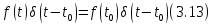
г) энергия δ-импульса бесконечно велика. Это легко показать, если воспользоваться одной из моделей дельта-функции – прямо­угольным импульсом длительностьюс амплитудой 1/

Рис. 3.2. δ-функция (а) и ее фильтрующее свойство (б) Рис. 3.3. Энергияδ-импульса

Энергия такого импульса пропорциональна квадрату его амплиту­ды и первой степени длительности(т. е. величине1/). При, когда прямоугольный импульс превращается в дельта­-функцию, его энергия становится бесконечно большой.

4.Прямоугольный симметричный импульсс единичной высотойRect(t/) (табл. 3.1, поз. 4), определяемый следующим образом:
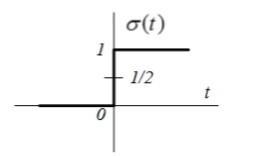
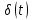