3. Спектральный анализ цепи

Комплексная передаточная функция цепи на какой-либо час­тоте вычисляется как отношение комплексной амплитуды реакции на этой частоте к комплексной амплитуде воздействия на этой же частоте.

При подключении цепи к источнику периодического напряжения комплексная передаточная функция цепи принимает раз­личные значения на частотах гармоник. Сравнение спектров ам­плитуд и фаз реакции и воздействия позволяет рассчитать коэф­фициенты передачи и фазовые сдвиги в цепи для каждой гармо­нической составляющей периодического сигнала.

Зная значения комплексной передаточной функции цепи на частотах гармоник периодического воздействия, можно вычис­лить реакцию цепи на это воздействие.

Задача определения изменения спектра периодического воздействия произвольной формы при прохождении его по цепи на­зывается задачей спектрального анализа цепи.Для расчета спектра реакции цепи необходимо определить спектр воздейст­вия, разложив периодический сигнал в ряд Фурье, вычислить комплексную передаточную функцию цепи на частотах гармоник, а затем найти спектр реакции, умножив спектр воздействия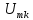на комплексную передаточную функцию,.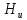

Комплексные амплитуды гармоник напряжения на резисторе в последовательном колебательном контуре рассчитываются по формуле

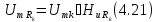
Чтобы вычислить амплитуды гармоник реакции, необходимо, в соответствии с (4.21), амплитуды гармоник воздейст­вия умножить на значения коэффициента передачи для этих гар­моник. Чтобы вычислить начальные фазы гармоник реакции це­пи, необходимо в соответствии с (4.21) к начальным фа­зам гармоник воздействия прибавить фазовые сдвиги, вносимые цепью на этих гармониках.

Амплитуды гармоник напряжения на резисторе в последова­тельном колебательном контуре

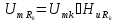, k = 0, 1, 3, 5, ... ,

а их начальные фазы

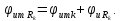
Зная спектры амплитуд и фаз реакции, можно рассчитать ре­акцию цепи, воспользовавшись ее представлением в виде ряда Фурье в тригонометрической (4.9) или комплексной (4.11) фор­ме, и установить, как изменилась форма воздействия при переда­че его по цепи.

Основные положения изложенных в п. 4.3 материалов:

• Задача спектрального анализа цепи состоит в определении того, как изменился спектр входного периодического сиг­нала при передаче его по цепи.

• Чтобы вычислить комплексные амплитуды гармоник напря­жения (тока) на элементе цепи, необходимо комплексные амплитуды гармоник входного напряжения (тока) умно­жить на значения комплексного коэффициента передачи для этих гармоник.

• Зная изменение спектра периодического сигнала при пере­даче по цепи, можно вычислить по формулам Фурье изме­нения формы сигнала.

4. Представление непериодического воздействия интегралом Фурье

Рассмотрим периодическую последовательность прямоуголь­ных импульсов (рис. 4.11, а). Увеличивая период Тэтой последо­вательности, легко перейти приТ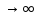от периодического сигнала к непериодическому (рис. 4.11,г).

Увеличение периода Тсигнала приводит к уменьшению час­тоты первой гармоники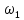=2π/Ти сгущению спектральных ли­ний. Уменьшаются также амплитуды гармоник поскольку остающаяся неизменной энергия сигнала распределя­ется теперь между возросшим числом гармоник и, естественно, доля каждой гармоники в общем сигнале падает (рис. 4.12).

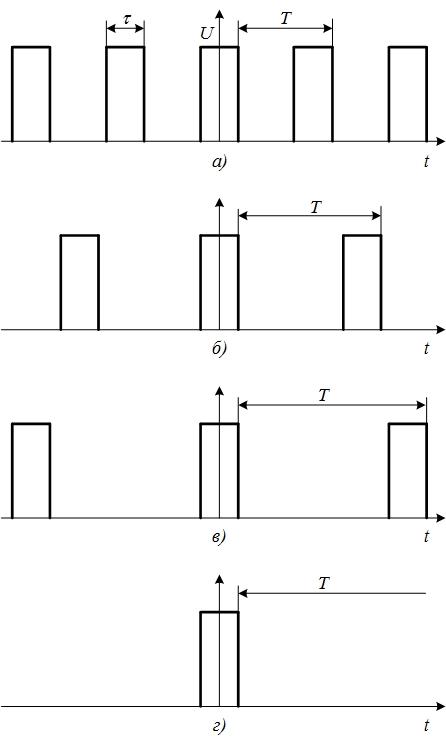
Рис. 4.11. Увеличение периода последовательности прямоугольных импульсов

При Т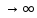 периодическая последовательность импульсов пе­реходит в одиночный импульс (рис. 4.11,г).В спектре такого сиг­нала вместо отдельных гармоник будет бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами и бесконечно малыми амплитудами. Другими словами, в любой бесконечно узкой полосе частот есть синусоидальное колебание бесконечно малой амплитуды.

Сравнивать между собой бесконечно малые величины не­удобно, поэтому вместо амплитуд (рис. 4.12) по оси ординат откладывают величину(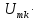Т)/2,которая при увеличении пе­риодаТостается неизменной. Введем новые обозначения для осей ординат на рис. 4.13:U(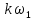) = 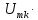(Т/2).В новых коорди­натах спектры сигналов (рис. 4.11) выглядят так, как показано на рис. 4.13,а–г. Спектр непериодического сигнала является в об­щем случае не дискретным, а непрерывным(сплошным).

Для комплексного спектра введенное на рис. 4.13 обозначение примет вид:

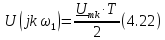
Ранее была получена пара преобразований (4.19) и (4.11) ,позволяющих найти спектр периодического сигнала 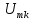и вос­становить периодический сигналu(t) по его спектру:

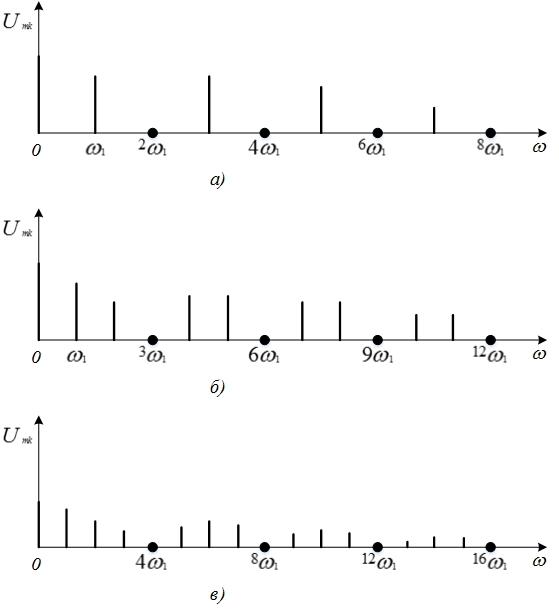
Рис. 4.12. Спектры амплитуд периодических последовательностей импульсов с разными периодами

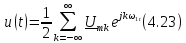
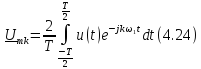
Получим подобную пару преобразований для непериодическо­го сигнала, изображенного на рис. 4.11, г.Для этого нужно в вы­ражении (4.24) устремить периодТк бесконечности и совершить в формулах (4.23) и (4.24) предельные переходы.

Сначала выразим из (4.1) комплексную амплитуду 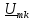в ви­де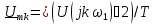и подставим ее в (4.23) и (4.24). Перепи­шем теперь эти выражения в виде

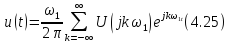
и

В выражении (4.25) учтено, что Т =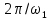.Затем устремим период к бесконечности (Т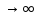). Гармоники будут сгущаться и дискретная частота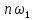перейдет в текущую частоту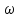, а значе­ние частоты первой гармоникибудет стремиться к бесконечно малой величинеd.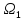

После предельного перехода получаем из (4.25) и (4.26)

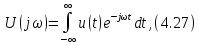
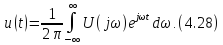
Уравнения (4.27) и (4.28) являются основными в теории спек­тров непериодическихсигналов, причем (4.27) называетсяпря­мым,а (4.28) -обратным преобразованием Фурье (интегралом Фурье). Взаимное преобразование Фурье символически обозначаетс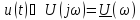я , где ≓ - знак соответствия этого преобразования.

Если вместо частоты ω использовать частоту f, то эти урав­нения примут вид.

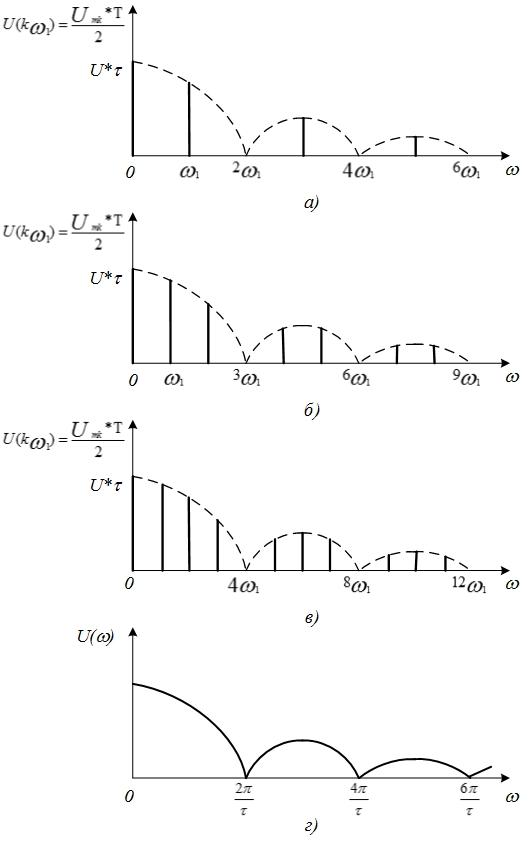
Рис. 4.13. Переход к спектральной плотности прямоугольного импульса

Основные положения изложенных в п. 4.4 материалов:

• Сигнал и его Фурье-изображение связаны парой инте­гральных преобразований, называемых преобразованиями Фурье.