
- •Оглавление
- •Общие сведения об электрических и радиотехнических цепях
- •Главные задачи электротехники и радиотехники
- •Радиотехнический канал связи
- •Классификация сигналов
- •Вопросы и задания для самопроверки:
- •Сигналы и их основные характеристики
- •Энергетические характеристики вещественного сигнала
- •Корреляционные характеристики детерминированных сигналов
- •Вопросы и задания для самопроверки:
- •Сигналы и спектры
- •Спектры сигналов
- •Простейшие разрывные функции
- •Методы анализа электрических цепей
- •Вопросы и задания для самопроверки
- •Спектральный анализ сигналов
- •Представление периодического воздействия рядом Фурье
- •Спектры амплитуд и фаз периодических сигналов
- •Спектральный анализ цепи
- •Представление непериодического воздействия интегралом Фурье
- •Спектральные плотности амплитуд и фаз непериодических сигналов
- •Примеры определения спектральной плотности сигналов
- •Определение активной длительности сигнала и активной ширины его спектра
- •Вопросы и задания для самопроверки:
- •Комлексная передаточная функция и частотные характеристики цепи
- •Спектральный анализ цепей при непериодических воздействиях
- •Вопросы и задания для самопроверки гл. 5, 6:
- •Представление непериодических сигналов интегралом лапласа
- •Вопросы и задания для самопроверки:
- •Электрические цепи радиотехнических сигналов
- •Цепи с распределенными параметрами
- •8.1.1 Длинные линии и телеграфные сигналы
- •8.1.2. Коэффициент отражения, стоячие и смешанные волны
- •8.1.3. Задерживающие цепи (Линия задержки)
- •Частотный принцип преобразования радиотехнических сигналов
- •8.2.1 Модулированные сигналы и их спектры
- •8.2.2. Электрические фильтры
- •8.2.3. Нелинейный элемент и воздействие на него одного сигнала.
- •8.2.4. Воздействие на нелинейный элемент двух сигналов.
- •Вопросы и задания для самопроверки:
- •Литература
- •107996, Москва, ул. Стромынка, 20
Корреляционные характеристики детерминированных сигналов
Одной из важнейших временных характеристик сигнала является автокорреляционная функция (АКФ), позволяющая судить о степени связи (корреляции) сигнала с его сдвинутой по времени копией.
Для
вещественного сигнала s(t),
заданного
на интервале времени (-∞,∞) и
ограниченного по энергии, корреляционная
функция (по энергии)
 определяется в единицах энергии следующим
выражением:
определяется в единицах энергии следующим
выражением:

где
 —
величина временного сдвига сигнала.
Интеграл (2.7) имеет вид свертки сигналаs(t)
с
его зеркальным изображением
—
величина временного сдвига сигнала.
Интеграл (2.7) имеет вид свертки сигналаs(t)
с
его зеркальным изображением
 т.е.
т.е.
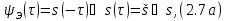
где ⊗˗ знак свертки сигнала ˗ сокращенной формы записи интеграла вида (2.7).
Для каждого значения τ автокорреляционная функция выражается некоторой числовой величиной.
Из (2.7) следует, что АКФ является четной функцией временного сдвига. Действительно, заменяя в (2.7) переменную (t - τ) на х, получим:

При
 = 0 сходство сигнала с его несдвинутой
копией и наибольшее и функция
= 0 сходство сигнала с его несдвинутой
копией и наибольшее и функция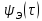 достигает
максимального значения, равного
полной энергииЭ
сигнала
достигает
максимального значения, равного
полной энергииЭ
сигнала

С
увеличением
 функция
функция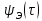 у
всех сигналов, кроме периодических,
убывает (не обязательномонотонно),
и при относительном сдвиге сигналов
у
всех сигналов, кроме периодических,
убывает (не обязательномонотонно),
и при относительном сдвиге сигналов
 и
и на величину, превышающую длительность
сигнала, обращается в нуль.
на величину, превышающую длительность
сигнала, обращается в нуль.

Рис.2.1. Построение автокорреляционной функции сигнала s(t) прямоугольной формы
Рис.
2.1 поясняет построение автокорреляционной
функции прямоугольного импульса
s(t),
который изображен на рис. 2.1,а. На рис.
2.1,б приведена сдвинутая на τ
(в сторону отставания) копия сигнала, а
на рис. 2.1,в – произведение

Автокорреляционная
функция для каждого значения
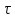 численно равна площади под кривой
произведения импульса и его сдвинутой
копии. Функция
численно равна площади под кривой
произведения импульса и его сдвинутой
копии. Функция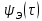 =
= (
( )
имеет вид треугольника с основанием
2
)
имеет вид треугольника с основанием
2 ,
высота которого определяется энергиейЭ
сигнала (рис. 1.2,г).
,
высота которого определяется энергиейЭ
сигнала (рис. 1.2,г).
Для
сигналов, обладающих бесконечно большой
энергией и ограниченных по мощности,
автокорреляционная функция
 определяется
в единицах мощности
определяется
в единицах мощности
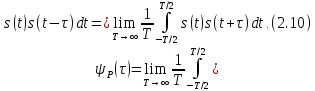
Соответственно
значение
 равно
средней мощности сигнала
равно
средней мощности сигнала

При определении
 периодической функции усреднение
выполняется по еепериоду
Ts,
т. е.
периодической функции усреднение
выполняется по еепериоду
Ts,
т. е.

Автокорреляционная
функция периодического сигнала сама
является периодической функцией с тем
же периодом. Действительно, поскольку
периодическая функция удовлетворяет
условию
 где
где – период, а
– период, а = 0,
1,
2,…,
то
= 0,
1,
2,…,
то

Например, для
гармонического сигнала s(t)
=A⋅cos( автокорреляционная функция выражается
в виде
автокорреляционная функция выражается
в виде

где
 .
.
При
 = 0 автокорреляционная функция
= 0 автокорреляционная функция (0)
=А2/2
определяет среднюю мощность
гармонического колебания с амплитудой
А.
Из полученного выражения следует, что
(0)
=А2/2
определяет среднюю мощность
гармонического колебания с амплитудой
А.
Из полученного выражения следует, что
 не
зависит от начальной фазы
не
зависит от начальной фазы
 колебания.
колебания.
В
табл. 2.1 приведены графики автокорреляционных
функций некоторых сигналов, определенные,
по энергии
 или
по мощности
или
по мощности

Для
оценки степени подобия двух сигналов
 (t)
и
s2(t)
используется
взаимная
корреляционная функция
(ВКФ), которая определяется выражением
(t)
и
s2(t)
используется
взаимная
корреляционная функция
(ВКФ), которая определяется выражением

Здесь
 и
и —
сигналы, заданные на бесконечном
интервале времени (-
—
сигналы, заданные на бесконечном
интервале времени (- ,
,
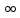 )и
обладающие конечной энергией. Выражение
(2.14) имеет вид свертки двух функций:
)и
обладающие конечной энергией. Выражение
(2.14) имеет вид свертки двух функций:

Значение
 не
меняется, если вместо задержки сигнала
не
меняется, если вместо задержки сигнала
 рассматривать
опережение первого сигнала
рассматривать
опережение первого сигнала .
Поэтому
вместо выражения (2.14) можно записать
общую формулу для определения ВКФ:
.
Поэтому
вместо выражения (2.14) можно записать
общую формулу для определения ВКФ:

т.
е.
 ,
но следует заметить, что
,
но следует заметить, что
Автокорреляционная
функция 𝜓( )
является частным случаем ВКФ
)
является частным случаем ВКФ ,
когда сигналы
,
когда сигналы одинаковы.
одинаковы.
В
отличие от
 ,
функция
,
функция в общем случае не является четной
относительно
в общем случае не является четной
относительно и может достигать максимума при любом
и может достигать максимума при любом .
.
Значение
 определяет взаимную энергию
определяет взаимную энергию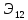 сигналов
сигналов


Таблица 2.1
|
№ п/п |
Вид
Сигнала s |
Вид
автокорреляционной функции
|
Примечание |
|
1 |
Гармоническое
колебание |
|
|
|
2 |
Прямоугольный
импульс
|
|
|
|
3 |
Треугольный
импульс |
|
_
|
|
4 |
Отрезок
меандра |
|
Огибающая
АКФ совпадает по форме с
|
|
5 |
Радиоимпульс |
|
Период
|
|
6 |
Последовательность прямоугольных импульсов
|
|
|
Основные положения изложенных в гл.2 материалов::
При анализе и синтезе цепей используют представления сигналов s в форме: временной функции
 ;
автокорреляционной (корреляционной)
функции𝜓(t);
спектральной функции
;
автокорреляционной (корреляционной)
функции𝜓(t);
спектральной функции
 (см. гл.4). В электротехнике и электронике
используют формы
(см. гл.4). В электротехнике и электронике
используют формы и
и
 в радиотехнике –
в радиотехнике – и𝜓(t).
и𝜓(t).Основной характеристикой любой формы представления сигнала s является энергия Э (или мощность Р).
Временная, корреляционная и спектральная формы сигнала преобразуются друг в друга по определенным формулам при условии равенства энергии при их преобразовании (равенство Парсеваля).
Два сигнала ортогональны (аддитивны) если их взаимная энергия (или мощность) равна нулю.





 –АКФ
по мощности. Имеет вид косинусоиды
независимо от начальной фазы сигнала
s
–АКФ
по мощности. Имеет вид косинусоиды
независимо от начальной фазы сигнала
s


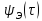 –АКФ
по энергии.
–АКФ
по энергии.
 – энергия сигнала.
– энергия сигнала.



 для прямоугольного импульса.
для прямоугольного импульса.

 совпадает с периодом
совпадает с периодом ,
форма огибаюΩей
АКФ совпадает с огибающей АКФ меандра.
,
форма огибаюΩей
АКФ совпадает с огибающей АКФ меандра.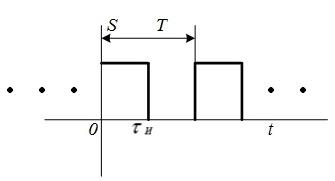

 –средняя
моΩность
сигнала
–средняя
моΩность
сигнала
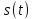 .
.