2. Частотный принцип преобразования радиотехнических сигналов

8.2.1 Модулированные сигналы и их спектры

В устройствах связи и в компьютерных сетях широко используется частотный принцип разделения сигналов. В соответствии с этим принципом сигналам отводятся неперекрывающиеся узкие полосы частот из всего диапазона частот, занимаемого системой передачи информации. С помощью узкополосных сигналов легко организовать передачу информации от большого числа источников к большому числу получателей, при этом источники не будут мешать друг другу.

Кроме частотного принципа в связи используется временной прин­цип разделения сигналов, когда каждому сигналу отводится неболь­шой промежуток времени из некоторого большого повторяющегося временного интервала, отведенного множеству сообщений. Времен­ной принцип часто используется в телефонии.

Частотный принцип разделения сигналов используется в радио- и телевещании, в устройствах мобильной связи, при передаче информа­ции с помощью модемов и т. п. Большинство узкополосных сигналов, располагаясь в области высоких частот системы связи, являются вы­сокочастотными колебаниями. Важное преимущество высокочастотных сигналов состоит в том, что они хорошо излучаются неболь­шими по размеру антенными устройствами и могут распространяться на большие расстояния.

Речевые и музыкальные сигналы, видеосигналы, сигналы, содер­жащие цифровую информацию и т. п., являются относительно низ­кочастотными сигналами. Их спектр занимает диапазон частот, начинающийся вблизи нуля и заканчивающийся некоторой верхней частотой. Например, телефонный речевой сигнал занимает диапазон частот от 300 Гц до 3400 Гц.

Проблема передачи информации, содержащейся во многих низко­частотных сигналах, с помощью множества узкополосных каналов связи с разными частотами решается при использовании модулиро­ванных сигналов. Модулированный сигнал — это узкополосный сиг­нал, параметры которого изменяются пропорционально низкочастот­ному информационному сигналу. Как правило, модулированный сигнал является высокочастотным колебанием. Для получения моду­лированного сигнала используется гармонический сигнал, называемый в этом случаенесущим колебанием (несущей частотой).Информация вносится в несущее колебание с использованиеммодуляции — изменения какого-либо из параметров высокочастотного сигнала пропорционально низкочастотному сигналуs(t). Различают три основных вида модуляции.

При амплитудной модуляции (AM) амплитуда сигнала изменяется прямо пропорционально информационному сигналу:

(8.17)

где — начальное значение амплитуды несущей,— ко­эффициент, зависящий от конструкции амплитудного модулятора. По определению амплитуда гармонического сигнала является положи­тельной величиной и поэтому в модулятореи должны быть такими, чтобы всегда. В противном случае возникаетпере­модуляция. Учитывая (8.17), сигнал сAMзаписываем следующим обра­зом

. (8.18)

Для анализа амплитудной модуляции удобно использовать про­стейшее сообщение — гармонический сигнал , (рис. 8.12, а). Формула (8.18) в этом случае принимает вид

(8.19)

где –коэффициент амплитудной модуляции. Коэф­фициентт – основной параметр АМ-колебаний с гармонической мо­дуляцией. На рис. 8.12б,в показаны модулированные сигналы с коэффициентамиAM, равнымит = 0,5 ит = 1 соответственно.

Рис. 8.12. Графики сигналов при АМ

При стопроцентной амплитудной модуляции имеют место макси­мальные изменения амплитуды модулированного сигнала: амплитуда изменяется от нуля до удвоенного значения.

Используя тригонометрическую формулу для произведения коси­нусов, выражение (8.19) перепишем в виде

(8.20)

Все три слагаемых в правой части формулы (8.20) — гармонические колебания. Первое слагаемое представляет собой исходное смодули­рованное колебание (несущую). Второе и третье слагаемые называют соответственно верхней и нижней боковыми составляющими. Форму­ла (8.20) дает спектральное разложение АМ-колебания. Амплитудный спектр АМ-сигнала изображен на рис.8.13, а. Ширина спектра этого АМ-колебания равна удвоенной частоте модулирующего сигнала.

Если модуляция осуществляется сложным периодическим сигна­лом, в спектре которого содержится много гармоник, то каждая из этих гармоник даст две боковые составляющие в спектре модулиро­ванного сигнала. В спектре появляются верхняя и нижняя боковые полосы (рис. 8.13, б). Ширина спектра будет определяться модулирую­щей гармоникой с максимально высокой частотой. Аналогичные ре­зультаты получим для сложного непериодического сигнала, используя теорему о спектре сигнала, умноженного на комплексный гармониче­ский сигнал.

Рис. 8.13. Амплитудный спектр сигналов при АМ

Отметим, что обе боковые полосы несут полную информацию о низкочастотном модулирующем сигнале. Поэтому в технике связи часто используются сигналы с одной боковой полосой (ОБП-сигналы). Нужная боковая полоса выделяется с помощью фильтра. Вторая боко­вая полоса (включая иногда и несущую) подавляется.ОБП-сигналы занимают меньшую полосу частот и при прочих равных условиях тре­буют меньшей мощности передатчика.

Фазовая модуляция (ФМ) — это изменение начальной фазы высо­кочастотного сигнала прямо пропорционально низкочастотному сиг­налу:

, (8.21)

где ˗ коэффициент, зависящий от конструкции фазового моду­лятора,˗ начальная фаза.

На практике наиболее часто использу­ется модуляция с большими отклонениями фазы от начального значе­ния.

С учетом (8.21) полная фаза (аргумент косинуса) при ФМ будет равна 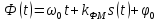. Из анализа этой формулы следует, что скорость возрастания полной фазы при ФМ не равна частоте несущей. Понятие частоты при ФМ требует уточнения.

Мгновенной частотой сигнала называют производную. У идеального гармонического сигнала мгновенная частота постоянна:. При ФМ мгновенная частота равна. Из этой формулы следует, что при ФМ в общем случае возникают изменения мгновенной частоты сигнала.

При частотной модуляции (ЧМ) мгновенная частота высокочас­тотного сигнала изменяется прямо пропорционально низкочастотному сигналу:

(8.22)

где ˗ коэффициент, зависящий от конструкции частотного модулятора.

График сигнала с ЧМ при гармоническом модулирующем сигнале приведен на рис. 8.14, б. Амплитуда сигнала с частотной модуляцией не изменяется. Увеличение уровня модулирующего сигнала вызывает увеличение мгновенной частоты сигнала. На рис. 8.14, б этому соответ­ствует увеличение числа максимумов и минимумов колебания на фик­сированном временном отрезке. При уменьшении мгновенной часто­ты сигнала увеличивается период квазигармонического сигнала.

Отметим, что график на рис. 8.14, б будет соответствовать сигналу с фазовой модуляцией ˗ при ФМ амплитуда сигнала также не изменя­ется, а при гармонической ФМ возникает гармоническая ЧМ. Кривая на рис. 8.14, а в этом случае соответствует производной от модулирую­щего сигнала.

Рис. 8.14. График сигналов при ЧМ

Второе слагаемое в формуле (8.22), содержащее сигнал s(t), как пра­вило, много меньше частоты несущей. Только в этом случае мо­дулированный сигнал будет относительно узкополосным и не будет "мешать" другим модулированным сигналам.

При частотной модуляции полная фаза сигнала определяется по формуле

Как видим, при ЧМ в общем случае изменяется начальная фаза сигнала. Выше отмечалось, что при ФМ имеются изменения мгновен­ной частоты. Поэтому ФМ и ЧМ ˗ два тесно связанных друг с дру­гом вида модуляции ˗ относят к угловой модуляции (УМ). Так как при модуляции высокочастотный сигнал близок к идеальному гармо­ническому сигналу, то модулированный сигнал называют также ква­зигармоническим сигналом.

Модулированный сигнал с фазовой модуляцией записывается сле­дующим образом

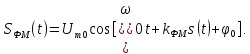(8.23)

Если в формуле (8.23) сигнал , то

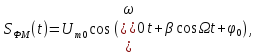(8.24)

где ˗индекс фазовой модуляции. Индекс фазовой модуля­циив (8.24) ˗ основной показатель сигнала с гармонической фазовой модуляцией. В системах связи, как правило, используются модулиро­ванные сигналы с большими значениями индекса фазовой модуляции:.

Используя введенное выше понятие мгновенной частоты, модули­рованный сигнал с частотной модуляцией запишем в виде

(8.25)

Если для модуляции используется простейший сигнал , то мгновенная частота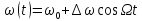, где – девиация частоты, равная максимальному отклоне­нию мгновенной частотыот . Девиация частоты- основной показатель сигнала с гармонической ЧМ. Формула (8.25) при гармо­нической частотной модуляции имеет вид

. (8.26)

Из анализа формулы (8.26) следует, что при гармонической ЧМ воз­никает гармоническая ФМ с индексом .

Для определения спектра сигнала с гармонической УМ используем формулу (8.24) для сигнала с ФМ. Выражение (8.26) также можно было бы использовать для расчета спектра сигнала с угловой модуляцией. Как известно, синус в (8.26) можно заменить косинусом с дополнительной начальной фазой, равной – 90°.

Для простоты при расчете спектра сигнала с угловой модуляцией начальную фазу в (8.24) примем равной нулю. Используя тригономет­рическое соотношение для косинуса суммы двух углов, формулу (8.24) перепишем в виде

, (8.27)

где определяются функцией˗ функция Бесселя первого родаn-го порядка.

Подставляя в (8.27), получим

(8.28)

….

Следовательно, при фазовой модуляции спектр колебания содер­жит несущую и бесконечное число гармонических составляющих, расположенных симметрично относительно несущей частоты (рис. 8.15). При использовании формулы (8.26) спектр ЧМ-сигнала будет отличать­ся от спектра ФМ-сигнала только начальными фазами отдельных спектральных компонент.

Рис. 8.15. Амплитудный спектр сигнала с УМ

Амплитуда несущей и амплитуды боковых составляющих в спек­тре сигнала с угловой модуляцией определяются функциями Бесселя. Если индекс угловой модуляции , то) и. Дру­гие функции Бесселя будут пренебрежимо малы. В этом случае в формуле (8.28) учитываются только несущая и две боковые гармоники и спектр колебания с угловой модуляцией похож на спектр сигнала сAM. Ширина спектра сигнала припримерно равна 2(рис. 8.15).

Если индекс , то дополнительные боковые составляющие об­разуют верхнюю и нижнюю боковые полосы. Причем амплитуда не­сущей уменьшается, а прии т. п. эта амплитуда равна нулю. В этом случае вся энергия модулированного сигнала сосредо­точена в боковых составляющих. Амплитудный спектр колебания с УМ при, равном примерно 2,4 и 5, приведен на рис. 8.15. Из анализа этих спектров и графиков рис. 8.14 следует, что ширина спектра сигнала с интенсивной угловой модуляцией припримерно равна удвоен­ной девиации частоты ().

Отметим, что использование угловой модуляции с большим ин­дексом позволяет получить увеличенную помехоустойчивость при передаче сложных сообщений. Сигналы с угловой модуляцией мень­ше подвержены влиянию импульсных помех, возникающих в про­мышленных электроустановках, при грозах, в транспортных средствах с электрическим питанием и т. п. Поэтому фазовая и частотная моду­ляции в настоящее время широко используются в радиовещании, в космической связи, в устройствах сотовой связи и в других системах передачи информации с малыми искажениями.

Для увеличения скорости передачи сообщений в современных сис­темах связи и передачи информации используются смешанные виды модуляции. Например, в модемах используется амплитудно-фазовая или квадратурная модуляции. При такой модуляции изменяется как амплитуда, так и начальная фаза (и частота) квазигармонического сигнала.