
- •Оглавление
- •Общие сведения об электрических и радиотехнических цепях
- •Главные задачи электротехники и радиотехники
- •Радиотехнический канал связи
- •Классификация сигналов
- •Вопросы и задания для самопроверки:
- •Сигналы и их основные характеристики
- •Энергетические характеристики вещественного сигнала
- •Корреляционные характеристики детерминированных сигналов
- •Вопросы и задания для самопроверки:
- •Сигналы и спектры
- •Спектры сигналов
- •Простейшие разрывные функции
- •Методы анализа электрических цепей
- •Вопросы и задания для самопроверки
- •Спектральный анализ сигналов
- •Представление периодического воздействия рядом Фурье
- •Спектры амплитуд и фаз периодических сигналов
- •Спектральный анализ цепи
- •Представление непериодического воздействия интегралом Фурье
- •Спектральные плотности амплитуд и фаз непериодических сигналов
- •Примеры определения спектральной плотности сигналов
- •Определение активной длительности сигнала и активной ширины его спектра
- •Вопросы и задания для самопроверки:
- •Комлексная передаточная функция и частотные характеристики цепи
- •Спектральный анализ цепей при непериодических воздействиях
- •Вопросы и задания для самопроверки гл. 5, 6:
- •Представление непериодических сигналов интегралом лапласа
- •Вопросы и задания для самопроверки:
- •Электрические цепи радиотехнических сигналов
- •Цепи с распределенными параметрами
- •8.1.1 Длинные линии и телеграфные сигналы
- •8.1.2. Коэффициент отражения, стоячие и смешанные волны
- •8.1.3. Задерживающие цепи (Линия задержки)
- •Частотный принцип преобразования радиотехнических сигналов
- •8.2.1 Модулированные сигналы и их спектры
- •8.2.2. Электрические фильтры
- •8.2.3. Нелинейный элемент и воздействие на него одного сигнала.
- •8.2.4. Воздействие на нелинейный элемент двух сигналов.
- •Вопросы и задания для самопроверки:
- •Литература
- •107996, Москва, ул. Стромынка, 20
8.1.2. Коэффициент отражения, стоячие и смешанные волны
Появление отраженных
волн при передаче сигналов с использованием
длинных линий, как правило, является
нежелательным явлением. Для оценки
интенсивности отраженных волн вводится
коэффициент
отражения(по напряжению)
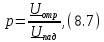
где
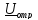 и
и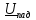 ˗ комплексные амплитуды отраженной и
падающей волн напряжения в произвольном
сечении линии. Так как токи и напряжения
в линии связаны с помощью волнового
сопротивления, то коэффициент отражения
для токов не вводится.
˗ комплексные амплитуды отраженной и
падающей волн напряжения в произвольном
сечении линии. Так как токи и напряжения
в линии связаны с помощью волнового
сопротивления, то коэффициент отражения
для токов не вводится.
Найдем
коэффициент отражения (8.7) в сечении
нагрузки. С учетом того, что в этом
сечении напряжение и ток в линии равны
току и напряжению на нагрузке, решения
телеграфных уравнений при
 принимают
вид
принимают
вид

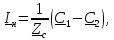
где
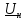 ,
,
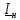 ˗
напряжение и ток через нагрузку. Из
первого выражения следует, что коэффициенты
˗
напряжение и ток через нагрузку. Из
первого выражения следует, что коэффициенты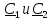 ˗ комплексные амплитуды напряжений
падающей и отраженной волн на нагрузке.
Разделив левые и правые части приведённых
соотношений друг на друга и учитывая,
что
˗ комплексные амплитуды напряжений
падающей и отраженной волн на нагрузке.
Разделив левые и правые части приведённых
соотношений друг на друга и учитывая,
что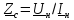 и
и
 получим следующую формулу для коэффициента
отражения в сечении нагрузки
получим следующую формулу для коэффициента
отражения в сечении нагрузки
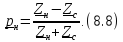
Из
выражения (8.8) получаем условие передачи
сигналов без отраженной волны:
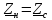 .
В этом случае
.
В этом случае
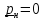 и в линии имеется только одна падающая
бегущая волна. Соотношение
и в линии имеется только одна падающая
бегущая волна. Соотношение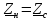 называютусловием
согласования
длиной линии и нагрузки, а получающееся
при этом состояние линии ˗ режимом
бегущей волны.
называютусловием
согласования
длиной линии и нагрузки, а получающееся
при этом состояние линии ˗ режимом
бегущей волны.
Для
линии с малыми потерями волновое
сопротивление равно вещественной
величине
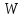 .
Например, на практике для построения
компьютерных сетей широко используются
двухпроводные линии с волновым
сопротивлением, равным
.
Например, на практике для построения
компьютерных сетей широко используются
двухпроводные линии с волновым
сопротивлением, равным
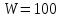 Ом.
Следовательно, для передачи всей энергии
от генератора (сервера) в нагрузку
(рабочую станцию) сопротивление нагрузки
должно быть равно 100 Ом.
Ом.
Следовательно, для передачи всей энергии
от генератора (сервера) в нагрузку
(рабочую станцию) сопротивление нагрузки
должно быть равно 100 Ом.
На
входе линии в режиме бегущей волны
существуют только напряжение и ток
падающих волн:
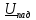 и
и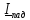 .
Их отношение дает входное сопротивление
линии
.
Их отношение дает входное сопротивление
линии ,
равное по определению волновому
сопротивлению
,
равное по определению волновому
сопротивлению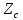 .
Для линий с малыми потерями
.
Для линий с малыми потерями
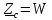 .
Передача максимума мощности от генератора
в нагрузку происходит при равенстве
входного сопротивления линии внутреннего
сопротивления генератора. Такой режим
называют режимом
согласования генератора с линией.
.
Передача максимума мощности от генератора
в нагрузку происходит при равенстве
входного сопротивления линии внутреннего
сопротивления генератора. Такой режим
называют режимом
согласования генератора с линией.
Рассмотрим
далее только линии с малыми потерями,
так как такие линии широко используются
на практике. У линий с малыми потерями
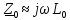 ,
,
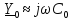 ,
,
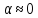 ,
,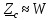 и
и
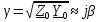 ,
где коэффициент фазы
,
где коэффициент фазы
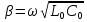 .
.
Коэффициент отражения в произвольном сечении линии с малыми потерями легко найти, используя решение телеграфного уравнения для напряжения в линии
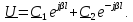
Разделив второе слагаемое, соответствующее отраженной волне, на первое слагаемое, соответствующее падающей волне, получим коэффициент отражения в произвольном сечении
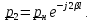
Этот
коэффициент отличается от
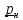 только
начальной фазой.
только
начальной фазой.
Пусть
в линии с малыми потерями модуль
коэффициента отражения
 .
Это случай полного отражения, при котором
вся энергия падающей волны отражается
от нагрузки. Из анализа формулы (8.8)
следует, что полное отражение возможно
в четырех случаях: на выходе линии
короткое замыкание
.
Это случай полного отражения, при котором
вся энергия падающей волны отражается
от нагрузки. Из анализа формулы (8.8)
следует, что полное отражение возможно
в четырех случаях: на выходе линии
короткое замыкание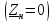 ,
на выходе линии холостой ход
,
на выходе линии холостой ход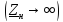 ,
нагрузка
линии ˗ катушка индуктивности
,
нагрузка
линии ˗ катушка индуктивности
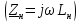 и
нагрузка линии ˗ конденсатор
и
нагрузка линии ˗ конденсатор
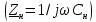 .
Такие нагрузки не потребляют энергии.
.
Такие нагрузки не потребляют энергии.
Зависимость результирующей амплитуды напряжения U в линии от расстояния l приведена на рис. 8.5 сплошной линией.
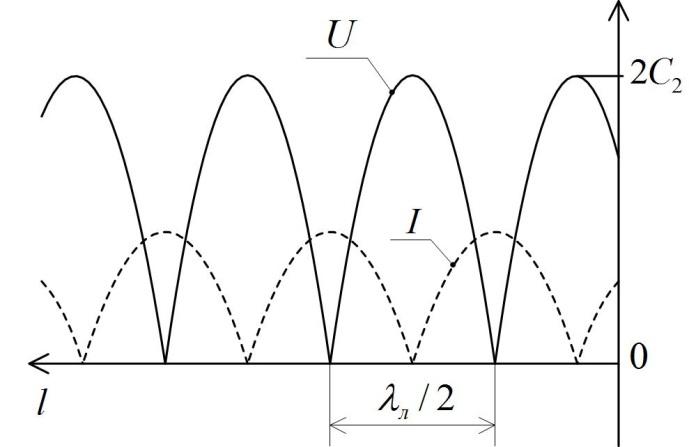
Рис 8.5. График изображения стоячей волны
Максимумы напряжения называются пучностями, а минимумы ˗узлами.Из постоянства начальной фазы результирующего напряжения в линии следует, что узлы и пучности в длинной линии с течением времени не перемещаются.
Волна, полученная в результате наложения падающей и отраженной волн при полном отражении, называется стоячей волной.Аналогичный вывод можно получить для тока в линии: при полном отражении возникает стоячая волна тока. Распределение амплитуды тока вдоль линии показано на рис. 8.5 пунктирной линией.
Стоячие волны в линиях передачи сигналов, как правило, нежелательны, так как в этом случае возникают повышенные напряжения в пучностях. Отрезки линии с полным отражением используются при создании СВЧ фильтров, согласующих устройств и колебательных систем.
Пусть в линии
имеет место неполное отражение ˗ часть
электрической энергии поступает в
нагрузку. Такой случай наиболее часто
встречается на практике. Амплитуда
отраженной волны
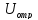 из-за частичного поглощения энергии в
нагрузке будет меньше амплитуды падающей
волны:
из-за частичного поглощения энергии в
нагрузке будет меньше амплитуды падающей
волны: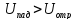 .
Представим падающую волну в виде двух,
составляющих:
.
Представим падающую волну в виде двух,
составляющих: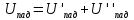 так что отраженная волна и первая часть
падающей волны образовывают стоячую
волну, а вторая часть падающей волны,
не взаимодействуя с отраженной, останется
бегущей падающей волной (рис. 8.6).
так что отраженная волна и первая часть
падающей волны образовывают стоячую
волну, а вторая часть падающей волны,
не взаимодействуя с отраженной, останется
бегущей падающей волной (рис. 8.6).
Волна, образованная суммой бегущей волны и стоячей волны, называется смешанной волной.
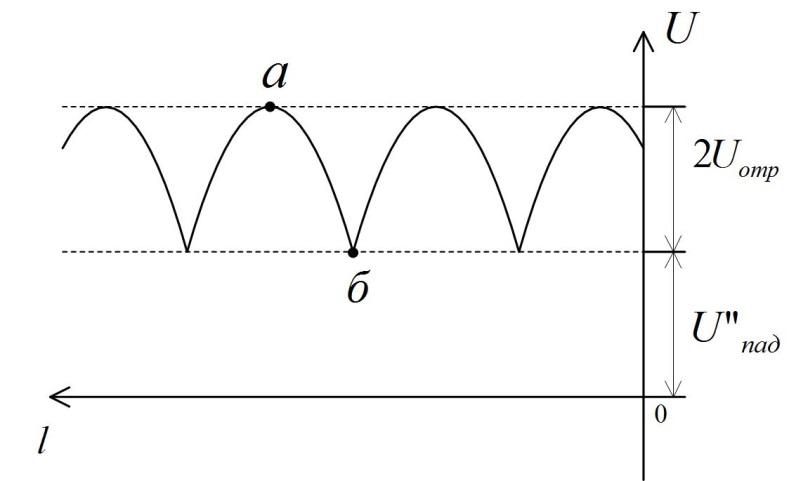
Рис. 8.6. График изображения смешанной волны
Распределение вдоль линии амплитуды напряжения в смешанной волне показано на рис. 8.6. В точке аимеется пучность, а в точкеб— узел напряжения в линии.Для описания смешанной волны используютсякоэффициент стоячей волны (КСВ) и коэффициент бегущей волны (КБВ):
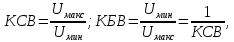
где
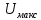 и
и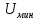 –
максимальное в пучности и минимальное
в узле напряжения в линии соответственно.
КСВ всегда больше или равен единице, а
КБВ всегда меньше или равен единице. В
системах передачи сигналов стремятся
получить КСВ или КБВ близкими к единице.
–
максимальное в пучности и минимальное
в узле напряжения в линии соответственно.
КСВ всегда больше или равен единице, а
КБВ всегда меньше или равен единице. В
системах передачи сигналов стремятся
получить КСВ или КБВ близкими к единице.
Из анализа кривых
рис. 8.6 следует, что
 ,
а
,
а
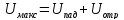 .Разделив максимальное значение напряжения
в линии на минимальное, получим формулу
взаимосвязи коэффициента отражения и
КСВ:
.Разделив максимальное значение напряжения
в линии на минимальное, получим формулу
взаимосвязи коэффициента отражения и
КСВ:
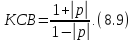
КСВ легко определить экспериментально, измеряя с помощью вольтметра напряжения в узлах и пучностях линии. В этом случае формулу (8.9) используют для расчета модуля коэффициента отражения.
На практике при построении компьютерных сетей и при использовании для передачи информации длинных линий мощность отраженной волны считается незначительной при КСВ < 2. Максимально допустимое значение модуля коэффициента отражения при этом не превышает 1/3.
