6. Спектральный анализ цепей при непериодических воздействиях

Представление непериодического сигнала в виде суммы бесконечного количества гармонических колебаний с бесконеч­но малыми амплитудами позволяет применить известные частот­ные методы, анализа цепей при синусоидальных воздействиях к расчету линейных электрических цепей при непериодических воздействиях произвольной формы. Предположим, задана элек­трическая цепь, в которой нужно определить реакцию в виде то­ков (t) или напряжений(t) ветвей на непериодическое воз­действие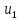(t). Для решения такой задачи необходимо прежде всего найти комплексную спектральную плотность воздействия, воспользовавшись прямым преобразованием Фурье (4.27), и комплексные сопротивления ветвейZ_k(jω). Теперь можно най­ти спектральные плотности реакций цепиI_k(jω), применив для расчета любой известный метод: законы спектра напряжений или токов Кирхгофа, методы свертывания, наложе­ния, контурных токов, узловых напряжений или эквивалентного генератора. Затем спектры реакцииI_k(jω) илиU_k(jω) _­­преобра­зуются в мгновенные значения токовi_k(t) или напряженийu_k(t) ветвей с помощью обратного преобразования Фурье (4.28).

Для определения реакции цепи в виде четырехполюсника при воздействии на входе цепи непериодического сигнала ис­пользуют комплексную передаточную функцию цепи. Как было установлено в §5, комплексная передаточная функция по на­пряжению (5.1) ˗ это отношение комплексных спектральных плотностей реакции и воздействия в цепи:

Зная комплексную спектральную плотность воздействия U­₁(j𝜔) и комплексную передаточную функциюH_u(j𝜔) цепи, легко найти комплексную спектральную плотностьU₂(jω) реак­ции цепи:

(6.1 а)

И используя известную теорему о свертке (4.38) и (7.10), получаем свертку

Все величины в уравнении (6.1) являются комплексными и могут быть записаны в показательной форме:

.

При этом уравнение (6.1 а) можно представить совокупностью двух уравнений:

(6.2)

(6.3)

из которых следует, что спектральная плотность амплитуд (ω) реакции цепи равна произведению спектральной плотности ам­плитуд(ω) воздействия и АЧХН_и(ω) цепи, а спектральная плотность фаз(ω) реакции цепи равна сумме спектральной плотности фаз(ω) воздействия и ФЧХ(ω) цепи.

После определения комплексной спектральной плотности u₂(ω) реакции цепи по формулам (6.1 а) или (6.2), (6.3) сама реакция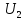(t) четырехполюсника может быть найдена с помощью обратного преобразования Фурье (4.28) или по таблицам преобразования Фурье.

Безыскаженная передача сигналовчерез линейную цепь возможна только при равномерной АЧХ и линейной ФЧХ цепи. Спектральный метод является достаточно эффективным и нагляд­ным при анализе передачи сигналов через линейную систему. Он позволяет оценить частотные искажения в канале связи, требова­ния к характеристикам электрической цепи. Особенно важно оп­ределить требования к АЧХ и ФЧХ цепи с точки зрения искаже­ния формы сигнала. Определим условия неискажаемой передачи сигнала через линейную систему. Предположим, что на входе ли­нейной цепи (четырехполюсника) действует сигнал опреде­ленной формы (рис. 6.1). На выходе в результате прохождения сигнала через четырехполюсник с комплексной передаточной функциейH(jω) амплитуда сигнала может измениться, и сигнал вследствие конечности скорости его распространения может за­паздывать относительно входного воздействия на.Однако важно, чтобы при этом не изменилась форма сигнала. Таким об­разом, условие безыскаженной передачи можно сформулировать с помощью равенства

(6.4)

где –некоторая вещественная постоянная;˗ время задерж­ки (запаздывания) выходного сигнала относительно входного.

Применив к (6.4) прямое преобразование Фурье и учтя свойство линейности и теорему запаздывания, перепишем условие (6.4) в частотной области:

(6.5)

Рис. 6.1. Сигнал на входе Рис. 6.2. АЧХ (а) и ФЧХ (б) четырехполюсника четырехполюсника

Так как комплексная передаточная функция цепи с учетом (5.1) должна быть

то отсюда получаем требование к АЧХ и ФЧХ неискажающей цепи:

(6.6)

,(6.7)

т.е. для того, чтобы линейная цепь не искажала форму сигнала, ее АЧХ должна быть равномерной (рис. 6.2,а), а ФЧХ линейной (рис.6.2,б).

Условие безыскаженной передачи во всем частотном диапа­зоне можно выполнить лишь для резистивных цепей. В цепях с реактивными элементами условия (6.6) и (6.7) можно обеспе­чить лишь в ограниченном частотном диапазоне ω₀(на рис. 6.2 показано штриховой линией).

Основные положения изложенных в гл. 6 материалов:

• Расчет спектров реакций цепи выполняется теми же методами, что и расчет цепи синусоидального тока.

• От спектров реакции к их мгновенным значениям можно перейти с помощью обратного преобразования Фурье.

• Спектр сигнала на выходе цепи находится как произведение спектра входного сигнала и комплексной передаточной функции цепи.

• Линейная цепь, имеющая равномерную АЧХ и линейную ФЧХ, не искажает форму сигнала, проходящего через нее.