
- •Оглавление
- •Общие сведения об электрических и радиотехнических цепях
- •Главные задачи электротехники и радиотехники
- •Радиотехнический канал связи
- •Классификация сигналов
- •Вопросы и задания для самопроверки:
- •Сигналы и их основные характеристики
- •Энергетические характеристики вещественного сигнала
- •Корреляционные характеристики детерминированных сигналов
- •Вопросы и задания для самопроверки:
- •Сигналы и спектры
- •Спектры сигналов
- •Простейшие разрывные функции
- •Методы анализа электрических цепей
- •Вопросы и задания для самопроверки
- •Спектральный анализ сигналов
- •Представление периодического воздействия рядом Фурье
- •Спектры амплитуд и фаз периодических сигналов
- •Спектральный анализ цепи
- •Представление непериодического воздействия интегралом Фурье
- •Спектральные плотности амплитуд и фаз непериодических сигналов
- •Примеры определения спектральной плотности сигналов
- •Определение активной длительности сигнала и активной ширины его спектра
- •Вопросы и задания для самопроверки:
- •Комлексная передаточная функция и частотные характеристики цепи
- •Спектральный анализ цепей при непериодических воздействиях
- •Вопросы и задания для самопроверки гл. 5, 6:
- •Представление непериодических сигналов интегралом лапласа
- •Вопросы и задания для самопроверки:
- •Электрические цепи радиотехнических сигналов
- •Цепи с распределенными параметрами
- •8.1.1 Длинные линии и телеграфные сигналы
- •8.1.2. Коэффициент отражения, стоячие и смешанные волны
- •8.1.3. Задерживающие цепи (Линия задержки)
- •Частотный принцип преобразования радиотехнических сигналов
- •8.2.1 Модулированные сигналы и их спектры
- •8.2.2. Электрические фильтры
- •8.2.3. Нелинейный элемент и воздействие на него одного сигнала.
- •8.2.4. Воздействие на нелинейный элемент двух сигналов.
- •Вопросы и задания для самопроверки:
- •Литература
- •107996, Москва, ул. Стромынка, 20
Комлексная передаточная функция и частотные характеристики цепи
Комплексная передаточная функция цепи — это важнейшая характеристика линейной электрической цепи в частотной области.
Электрическую
цепь удобно изображать в виде
четырехполюсника (рис. 5.1), на входные
зажимы (1 —
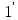 )
которого подается воздействие в виде
напряжения
)
которого подается воздействие в виде
напряжения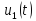 или
тока
или
тока
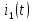 ,имеющих
комплексные спектральные плотности
,имеющих
комплексные спектральные плотности
 и
и
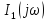 ,а
реакция цепи снимается с выходных
зажимов
,а
реакция цепи снимается с выходных
зажимов
 также в виде напряжения
также в виде напряжения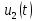 или тока
или тока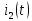 ,имеющих
комплексные спектральные плотности
,имеющих
комплексные спектральные плотности
 и
и
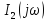 .
Комплексная передаточная функция
определяется как отношение комплексной
спектральной плотности реакции цепи к
комплексной спектральной плотности
воздействия.
.
Комплексная передаточная функция
определяется как отношение комплексной
спектральной плотности реакции цепи к
комплексной спектральной плотности
воздействия.
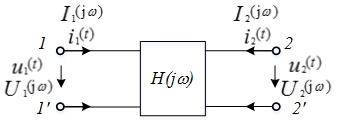
Рис. 5.1. Четырехполюсник
В зависимости от типов воздействия и реакции различают следующие виды комплексных передаточных функций: комплексная передаточная функция по напряжению

комплексная передаточная функция по току
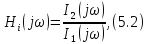
комплексное передаточное сопротивление
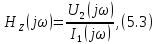
комплексная передаточная проводимость
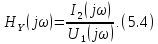
Функции
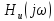 и
и
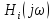 являются безразмерными величинами,a
являются безразмерными величинами,a
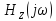 и
и
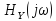 имеют соответственно размерности
сопротивления и проводимости.
имеют соответственно размерности
сопротивления и проводимости.
Комплексные передаточные функции цепи определяются на каждой частотной составляющей непериодического воздействия сложной формы.
Представление непериодических сигналов в форме интеграла Фурье (4.41) позволяет применить к бесконечно малым гармоникам, составляющим их спектр, методы анализа, рассмотренные в электротехнике. В частности, законы Ома и Кирхгофа для спектров будут иметь вид:

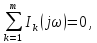
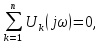
где
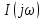 ,
, – спектры токов и напряжений ветвей
соответственно;
– спектры токов и напряжений ветвей
соответственно;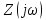 и
и
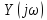 имеют
смысл комплексных сопротивлений и
проводимостей ветвей.
имеют
смысл комплексных сопротивлений и
проводимостей ветвей.
Законы Ома и Кирхгофа для спектров позволяют распространить рассмотренные методы анализа цепей при гармонических и периодических несинусоидальных воздействиях на непериодические сигналы.
Найдем комплексную передаточную функцию по напряжению последовательного колебательного контура, изображенного на рис. 5.2.
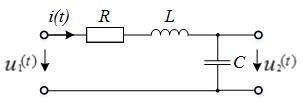
Рис. 5.2 Последовательный колебательный контур
Комплексная передаточная функция по напряжению в цепи, изображенной на рис. 5.2, есть отношение комплексных спектральных плотностей напряжения на емкости и входного напряжения:
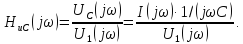
Комплексную
спектральную плотность тока
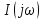 в цепи рассчитывают, используя закон
Ома для спектров:
в цепи рассчитывают, используя закон
Ома для спектров:

Подставляя
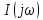 в выражение для расчета
в выражение для расчета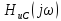 ,
получаем
,
получаем
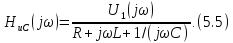
Очевидно,
что комплексная передаточная функция
 зависит только от частоты и параметров
цепи. Этот вывод справедлив и для любых
других передаточных функций.
зависит только от частоты и параметров
цепи. Этот вывод справедлив и для любых
других передаточных функций.
Как
всякую комплексную величину,
 можно представить в показательной
форме:
можно представить в показательной
форме:
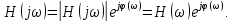
Модуль
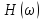 комплексной передаточной функции
называетсяамплитудно-частотной
характеристикой
цепи
(АЧХ), а аргумент комплексной
передаточной функции
комплексной передаточной функции
называетсяамплитудно-частотной
характеристикой
цепи
(АЧХ), а аргумент комплексной
передаточной функции
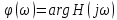 называетсяфазо-частотной
характеристикой
цепи (ФЧХ).
называетсяфазо-частотной
характеристикой
цепи (ФЧХ).
Амплитудно-частотная характеристика цепи определяет степень изменения спектральной плотности амплитуд входного сигнала при передаче его по цепи.
Фазо-частотная характеристика цепи определяет степень изменения спектральной плотности фаз входного сигнала при передаче его по цепи.
Для примера найдем АЧХ и ФЧХ цепи, изображенной на рис. 5.2, если R = 2 Ом, L= 0,704 мГн, С = 4 мкФ.
АЧХ и ФЧХ последовательного колебательного контура определим, воспользовавшись (5.5):

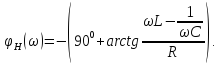
Подставляя
в
 и
и
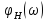 параметрыR,
L,
С
и значение
параметрыR,
L,
С
и значение
 ,
получаем
,
получаем

 .
.
Графики
АЧХ
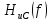 и
ФЧХ
и
ФЧХ приведены на рис. 5.3.
приведены на рис. 5.3.
Из этих графиков следует, что, например, на частоте f = 3 кГц (резонансная частота контура) амплитуда напряжения на конденсаторе возрастает в 6,3 раза, а фаза напряжения на конденсаторе изменяется на -90° по сравнению с амплитудой и фазой входного напряжения. Аналогичным образом можно на каждой частоте определить изменение спектрального состава сигнала при передаче его по цепи.
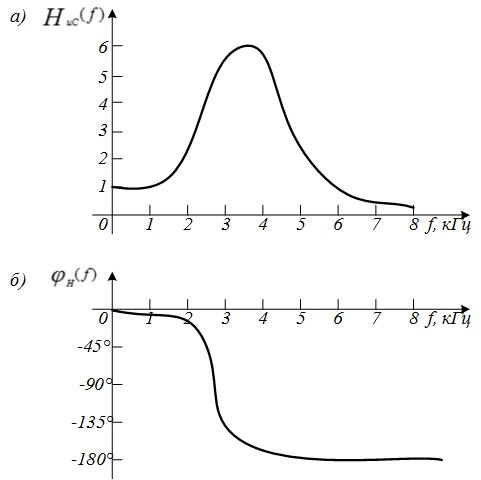
Рис. 5.3. АЧХ и ФЧХ последовательного колебательного контура
В ряде случаев частотные характеристики цепи могут изменяться в довольно широких пределах, поэтому более удобно их оценивать в логарифмическом масштабе. С этой целью для оценки АЧХ вводят понятие логарифмической амплитудно-частотной характеристики (ЛАХ):

Значения величиныК оцениваются в децибелах (дБ). В активных цепях величину К также называют логарифмическим усилением. В пассивных цепях вместо коэффициента усиления используют понятие ослабления цепи (A):
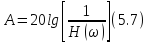
которое также оценивается в децибелах.
Для
примера
определим
пределы
изменения логарифмической
амплитудно-частотной характеристики
цепи, если ее АЧХ
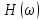 принимает
значения от 1 до 10000.
принимает
значения от 1 до 10000.
Для
определения значений ЛАХ воспользуемся
выражением (5.5). Значению
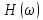 = 1 соответствуетК
= 20
lg
= 1 соответствуетК
= 20
lg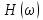 =
0 дБ. Значению
=
0 дБ. Значению
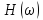 = 10000
соответствует К
= 20 lg
(10
000) = 80 дБ. Характеристику, изменяющуюся
от 0 до 80 дБ, легко изобразить графически.
= 10000
соответствует К
= 20 lg
(10
000) = 80 дБ. Характеристику, изменяющуюся
от 0 до 80 дБ, легко изобразить графически.
Основные положения изложенных в гл. 5 материалов:
Частотная характеристика показывает, как ведет себя цепь на разных частотах: АЧХ показывает изменение амплитуды каждой частотной составляющей входного сигнала при передаче по цепи; ФЧХ показывает сдвиг фаз каждой частотной составляющей.
Логарифмические частотные характеристики удобны для специалистов, так как логарифмические характеристики изменяются в менее широких пределах, чем АЧХ.
