Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет прикладной биотехнологии

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Наврозов, В. В. Элементы высшей математики 2

.pdf

Скачиваний:

Добавлен:

09.04.2015

Размер:

796.53 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Вятская государственная сельскохозяйственная академия» Кафедра математики

В.В. Наврозов, Т.В. Малых

Элементы высшей математики 2

Интегральное исчисление. Дифференциальные уравнения

Учебное пособие для студентов биологического факультета

Киров 2012 1

УДК 517.2 ББК 22.161.11

Наврозов В.В., Малых Т.В. Элементы высшей математики 2. Интегральное исчисление. Дифференциальные уравнения: Учебное пособие

для студентов биологического факультета. Киров: ФГОУ ВПО Вятская ГСХА, 2012. 33 с.

Рецензенты: доцент кафедры математики Вятской ГСХА, кандидат физикоматематических наук Фарафонов В.Г.; доцент кафедры математического моделирования в

экономике ВятГУ, кандидат физикоматематических наук Ковязина Е.М.

Методические указания рассмотрены и утверждены методической комиссией инженерного факультета Вятской государственной сельскохозяйственной академии (протокол № 8 от 3 мая 2012г.).

В методических указаниях рассмотрены основные понятия интегрального исчисления, методы решения некоторых обыкновенных дифференциальных уравнений первого порядка, приведены примеры решения задач, упражнения для самостоятельной работы и контрольные задания.

Наврозов Виктор Васильевич, Малых Татьяна Викторовна, 2012ФГОУ ВПО Вятская ГСХА, 2012

	Оглавление
1. Неопределенный интеграл.....................................................................		4
1.1	Свойства неопределенного интеграла.............................................	4
1.2	Таблица основных неопределенных интегралов ..........................	5
1.3	Методы интегрирования ..................................................................	6
1.4	Интегралы от функций, содержащих квадратный трехчлен .....	11
2. Определенный интеграл ......................................................................		15
2.1	Свойства определенного интеграла...............................................	15
2.2	Замена переменной и интегрирование по частям в определенном
интеграле ................................................................................................		17
2.3	Вычисление площадей плоских фигур .........................................	19
3. Дифференциальные уравнения первого порядка..............................		20
3.1	Общие понятия ................................................................................	20
3.2	Уравнения с разделяющимися переменными ..............................	21
3.3	Однородные дифференциальные уравнения ................................	22
3.4	Линейные уравнения первого порядка .........................................	24
3.5	Уравнения Бернулли .......................................................................	27
4. Контрольные задания ...........................................................................		29

1. Неопределенный интеграл


Определение. Функция			F x
функции	f x на интервале		a,b ,
интервала выполняется равенство
		F x
Утверждение. Если		F1 x и
функции	f x на интервале		a,b ,

называется				первообразной	от
если		во	всех точках x этого
f x .
F2	x	–	две	первообразные	от
то	разность			между ними равна

некоторому постоянному числу.						f x
	Из утверждения следует, что если для данной функции
найдена какая нибудь первообразная				F x , то	любая другая
первообразная для f x имеет вид F x C , где C const .
	Определение. Если функция F x			является первообразной для
f x ,	то совокупность	F x C	называется		неопределенным

интегралом от функции f x и обозначается		f x dx .
интегралом от функции f x и обозначается		f x dx .
При этом функцию f x называют подинтегральной функцией,
f x dx подинтегральным выражением, знак		знаком интеграла.
По определению

f x dx

F x C

если

F x

(1.1)

С геометрической точки зрения неопределенный интеграл представляет собой совокупность кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вдоль оси Oy .

	1.1 Свойства неопределенного интеграла
1.	Дифференциал	от	неопределенного		интеграла	равен
подинтегральному выражению
			f x dx f	x dx.
		d	f x dx f	x dx.
2.	Неопределенный	интеграл от		дифференциала некоторой

функции равен сумме этой функции и произвольной постоянной:

dF x F x C .

3.Постоянный множитель можно выносить за знак интеграла, т.е.

если

const

, то

kf x dx k

x dx

4. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме неопределенных интегралов от каждой из этих функций:

f x g x

p x dx

f x dx g x dx

p x dx

Эти свойства следуют из определения интеграла (1.1) и правил дифференцирования.

1.2 Таблица основных неопределенных интегралов

0dx C

x C

C , R, 1

ln x C

dx e

C, a 0, a 1

ln a

7.sin xdx cosx C

8.cos xdx sin x C

9.	dx		tgx C

	2
	cos	x

10.

ctgx C

sin

11.

tgxdx ln cosx C

12.

ctgxdx ln sin x C

13.

arctg

C ,

a 0

14.

a x

C , a 0

a x

15.

arcsin

C ,

a x a, a 0

16.

ln x

C ,

a 0

17.

shxdx chx C

18.

chxdx shx C

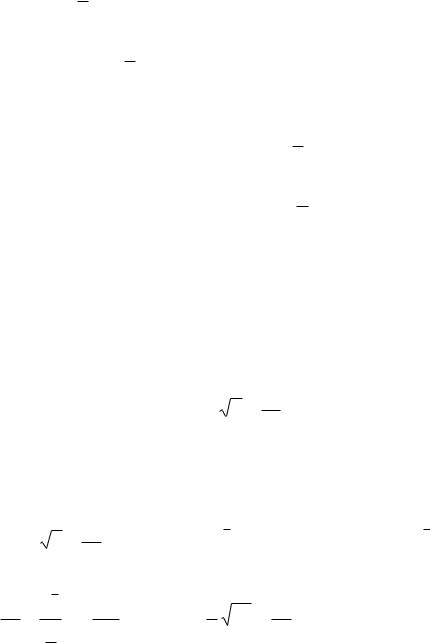
При нахождении неопределенных

иметь в виду следующие правила (если

интегралов

f x dx F x

бывает полезно

C ):

I.	f kx dx	1	F kx
		k

III.	f kx b dx			1
				k

Например:

C .kx

kx dx

II.

1	e	kx

k

xb dx

C ;

F x

b C

sin kx b dx

1 cos kx b k

1.3 Методы интегрирования

I. Непосредственное интегрирование.

Этот метод основан на использовании свойств неопределенного интеграла и таблицы основных интегралов.

Пример. Найти

	2	x
3x		x

4
x	3

dx

Решение. Сначала преобразуем подинтегральную функцию, затем применим свойства 3, 4 неопределенного интеграла и табличный интеграл 3.

								4								1										1
																1										1
	3x		2			x							2	x			4x				3	dx		2	dx x		dx 4 x	3	dx
	3x					x				dx 3x				x		2	4x					dx		3 x	dx x	2	dx 4 x		dx
								x	3
								x

						3
		x	3		x	2			x	2		3			2			3			2
3		3			3		4		2		C x				3		x				x		C.


																					2
					2
																		2
				Пример. Найти 3sin x																dx .
				Пример. Найти 3sin x																dx .
																			x

Решение. Применяя свойства 3, 4 неопределенного интеграла и табличные интегралы 4, 7, получим

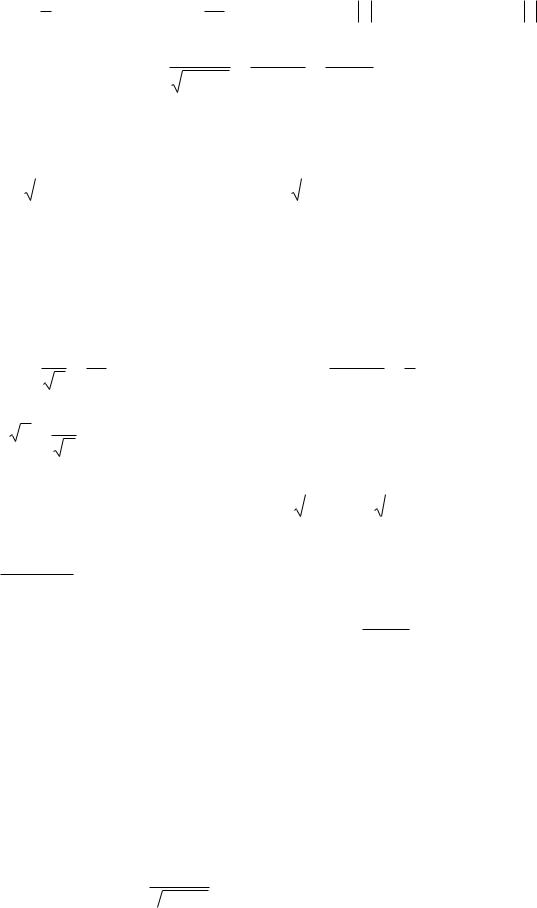
	2	dx	3 cosx 2ln x C 3cosx 2ln x C.
3sin x	dx 3 sin xdx 2		3 cosx 2ln x C 3cosx 2ln x C.
	x	x

Пример. Найти

6		5
	2		2
9 x	2	16 x	2
9 x		16 x

1 4 x2

dx

Решение. Применяя свойства 3, 4 неопределенного интеграла и табличные интегралы 13, 14, 15, получим


	6					5			1									dx						dx				dx
	6					5			1									dx						dx				dx
													dx		6						5
					16 x			2	4 x		2												2	x	2		2	x	2
	9 x	2						2			2						3	2	x	2		4	2		2	2	2		2
	9 x																3		x			4				2
6 arcsin				x		5	arctg			x		1		ln		2 x	C.
				x		5				x		1				2 x
																2 x
			3			4			4			4				2 x

Упражнение 1. Найти неопределенные интегралы:

1)				1	3
	2x					4	dx
				x	x

				1	2
3)			x		dx ;

				x
5)	x	2	1 x 4 dx ;

;

2)
2)

2	x				4					3
2					16 x		2					dx ;
							2			x
										x
			3
						5sin x dx ;
sin 2						5sin x dx ;
sin 2					x
				2					1				5
															dx ;
															dx ;
		x		2	5			x	2		4		25 x	2
		x			5			x			4		25 x

			2		x
7)	2 cos				x	dx ;
7)		2	x			dx ;
	cos		x
	2 x
			3
9)	x	2		dx ;
		2

II. Интегрирование подстановки).

8)	5
10)

методом

 

6x	5	dx ;
6x		dx ;
3tgx			4
3tgx			x
		9	x

замены


	2	dx .
	2

переменной (способ

Пусть	требуется
переменной	x t , где

dx d t	t dt . Тогда

найти

интеграл f x dx . Сделаем замену дифференцируемая функция; найдем

f x dx

t t dt

Пример. Найти dx .

5 3x

Решение. Делаем замену переменной:

5 3x t 5 3x t	2	;	d 5 3x dt	2	3dx 2tdt
	2			2

2 tdt

Получим:


	dx	dx	2		tdt
	5		3		t
		3x
Пример. Найти sin			3	x cos

Решение. Замечаем, что Удобно замену переменой непрерывной записи:

	2	dt	2	t C	2	5	3x C .
	3		3		3

xdx .
cosxdx d sin x , и делаем замену:

и последующие преобразования

sin	3	x cos xdx		sin x t					t	3	dt	1	t	4	C	1	sin	4	x C.
	3									3				4				4
				cos xdx dt								4				4
				cos xdx dt								4				4
				e	x	dx
Пример. Найти				e		dx		.
Пример. Найти			e	x	e		x	.
				x			x

sin x t .

вести в

Решение. Преобразуем и делаем замену переменной:

ln t

1 C

2 x

dx dt

ln e

2 x

Упражнение 2. Найти неопределенные интегралы:

2	dx
5

;

3	2x

1dx

;

dx2 7x 8

;

4)		sin xdx	;

	4	cos2 x

5)	e		x	3	x	2	dx ;


9)		ln 3 xdx						;

					x
13)				4x 3
						x

;

xdx

arcsin

;

1 x

arctgx

;

1 x

cos xdx

xdx

10)

;

11)

;

12)

x 2

dx ;

sin 2 x 3

x 2

14)

;

15) x2

x3 1dx .

III. Метод

Пусть

интегрирования по частям.

u x и v v x дифференцируемые функции. По

правилам дифференцирования произведения найдем d u x v x v x du x u x dv x .

Интегрируем почленно и, учитывая, что d u x v x u x v x , находим

u x dv x u x v x

v x du x

(1.2а)

Последняя формула обычно записывается в зависящем от обозначения переменной:

udv uv vdu.

инвариантном виде, не

(1.2)

Формула (1.2) называется формулой интегрирования по частям.

Указание 1. Если подинтегральное выражение содержит произведение показательной или тригонометрической функции на многочлен, то в качестве множителя u следует принимать многочлен.

Указание 2. Если подинтегральное выражение содержит произведение логарифмической или обратной тригонометрической функции на многочлен, то в качестве множителя u следует принять логарифмическую или обратную тригонометрическую функцию.

Пример. Найти x sin xdx .

Решение. Полагаем, что

u x,

sin xdx

, тогда

du dx, v sin xdx

cosx

(берем частное решение,

Удобно решение оформлять так (используя формулу (1.2)):

u x

du dx

xsin xdx

x cosx

cosxdx

cosx

dv sin xdx

1	x cosx	1	sin x C.
	x cosx		sin x C.
		2

Пример. Найти arctgxdx .

Решение. Полагаем, что

arctgx

, получим

arctgxdx

u arctgx

xarctgx

xdx

1 x2

dv dx

v x

2xdx dt

xarctgx

C xarctgx

x 2 ln xdx .

Пример. Найти

Решение. Полагаем, что

u ln

, получим

x 2 ln xdx u ln x	du		dx
					1	x2	2x ln x
				x	1
		1		x2 2x	2
dv x 2 dx v		1			2
dv x 2 dx v		2
		2
				9

1	x	2	2x dx	1	x

2			x	2

Пример. Найти

x

2 2

x ln x	1	x
x ln x	2	x
	2
3x 2 e			2x	dx
3x 2 e				dx

2 dx	1	x	2	2x ln x	1	x	2	2x C.
2 dx		x		2x ln x		x		2x C.

	2				4

Решение. Здесь дважды применяем интегрирование по частям:

u x

3x 2 du 2x 3 dx

3x 2 e

2 x

dv e

2 x

2x 3 e

u 2x 3

du 2dx

2 e

2x 3 e

2 x

dv e

2 x

3x 2 e

2 x

3 e

2 x

2x 3 e

2 x

Пример. Найти e	4x	sin 3xdx .

Решение. Дважды применим метод интегрирования по частям:

u e

4 x

du 4e

4 x

sin 3xdx

4 x

cos3x

dv sin 3xdx

cos3xdx

u e

4 x

cos3xdx

4 x

cos3x

4 x

sin 3x

cos3xdx

sin 3xdx

4 x

sin 3xdx.

Тогда

4 x

sin 3xdx

4 x

cos3x

4 x

sin 3x

4 x

sin 3xdx .

Выразим из этого равенства

4 x

sin 3xdx

4 x

sin 3xdx

4 x

sin 3x

4 x

cos3x

4sin 3x 3cos3x

4 x

sin 3xdx

4 x

4sin 3x

3cos3x

xsin

3xdx

Упражнение 3. Найти неопределенные интегралы:

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.07.2019397.31 Кб0Метрология.Журнал лабораторных работ.doc
#
03.11.2018971.26 Кб27Метрология.Методичка.doc
#
12.11.20182.24 Mб23Метрология.МИСТ11.doc
#
09.04.2015236.61 Кб28микра.docx
#
09.04.20151.2 Mб28МУ-РГР-Детали машин.pdf
#
09.04.2015796.53 Кб8Наврозов, В. В. Элементы высшей математики 2.pdf
#
31.08.2019628.22 Кб2Новый2.doc
#
26.11.2019336.38 Кб5Нормы - клиника, биохимия, кал.doc
#
09.04.2015460.29 Кб35обработка измерений.doc
#
09.04.201589.6 Кб13Обществознание 2013.doc
#
14.08.2019278.53 Кб3Однородные преобразования.doc