Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет прикладной биотехнологии

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Наврозов, В. В. Элементы высшей математики 2

.pdf

Скачиваний:

Добавлен:

09.04.2015

Размер:

796.53 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

1)	xe	x	dx ;

4)	arcsin xdx

;

2)

5)

ln x

e	x	dx ;

1 dx ;

3)
6)

x	3	ln xdx

ln x		dx ;
x	2

;

7) x2xdx ;

10)

ln xdx

;

8) x2 cos3xdx ;

11)	2
11)	x 1	sin xdx

;

9) e3x cosxdx ;

12)	3	x	cosxdx .

1.4 Интегралы от функций, содержащих квадратный трехчлен

Рассмотрим интегралы вида:

;

Ax B

dx ;

Ax B

dx ;

bx cdx , где

bx c

a,b,c, A, B R, a 0 .

Для отыскания указанных интегралов нужно в выражении

bx c

выделить полный квадрат и заменить основание квадрата новой переменной.

Пример. Найти

	x	2

dx2x 5

			Решение.	Выделив							в			знаменателе					полный
x	2	2x 5 x		2	4 x			2		2			2	и введя новую переменную
				1			1
dx dt , получим
			dx		dx				dt					1	arctg	t	C	1	arctg	x 1	C .
		2	2x 5	x	2			2				2
	x					4	t				2			2		2		2		2
					1

квадрат

x 1 t ,

Пример. Найти						4 3x				dx .
Пример. Найти						2				dx .
				3x		2	4x 1
				3x			4x 1
Решение. Выделим в знаменателе полный квадрат:
												2						2
	x2	4	x		1		3		x		2		4	1	3	x	2
3x2 4x 1 3	x2		x				3		x						3	x

		3			3						3		9	3			3


введем новую переменную								x		2	t, dx dt .
введем новую переменную								x		3	t, dx dt .
										3

Тогда

	1
	1
	9
	9

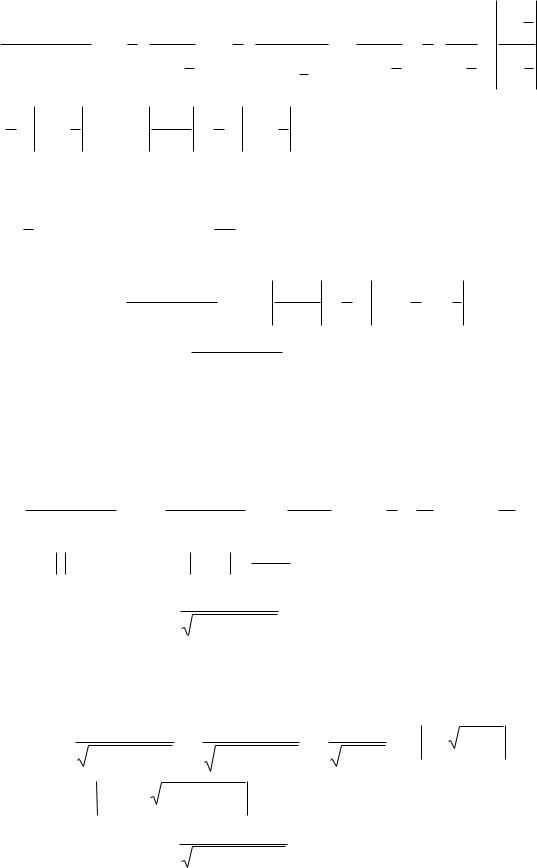
																										t	1
			4 3x					1	2 3t					2			dt			tdt		2	1			t	3
			4 3x				dx	1	2 3t		dt			2			dt			tdt		2	1		ln

			2							1									2		1			1			1
3x				4x 1				3	t 2	1				3		2		1		t 2	1	3	2	1		t	1
3x				4x 1				3	t 2					3	t	2		1		t 2		3	2			t
										9					t						9			3			3
										9								3			9			3			3
																		3
	1	ln t			2	1	C ln		3t 1			1	ln t		2		1	C.
		ln t					C ln						ln t					C.

	2					9			3t 1			2					9

Первый интеграл здесь нашли по формуле (14). Второй методом замены привели к интегралу 4 (подстановка

u, 2tdt du

tdt

Окончательно, возвращаясь к переменной

4 3x

dx ln

3x 3

ln x

3x 1

Пример. Найти

2x 1

dx .

8x 16

Решение. Выделим полный квадрат

Введем новую переменную x 4 t,

, получаем

4 x 1 C .

3 3

8x 16 x

dt .

4 2

Применяя свойства неопределенного интеграла и таблицу основных неопределенных интегралов, получим

			2x 1		dx
	x	2	8x 16

2ln t 9t				1	C

Пример. Найти

2 t
	t
2ln x
	x

4 1		dt
2

4		x

	dx
2	2x

	2t 9		2	9			dt	9 t	2	dt
	t	2	dt	t	2	dt 2	t	9 t		dt
	t		t	t			t
9	C.
	C.
4
.
3

Решение.

x	2	2x 3	x

Получим

Выделим в подкоренном выражении

2	2	, введем новую переменную
1

полный квадрат

x 1 t dx dt .

ln x 1

Пример. Найти

2x 1

9 6x 3x

		dt		ln t	t	2	2 C
						2
2	t	2	2
2	t		2

dx .

Решение. Выделим в подкоренном выражении полный квадрат:

9 6x 3x2 3 x2 2x 3 3 x 1 2 4 3 4 x 1 2 . 12

Введем новую переменную

x 1 t, dx dt .

2x 1

2t 1

dt .

9 6x 3x2

4 x 1 2

4 t2

Разложим полученный интеграл на разность двух интегралов и каждый найдем по отдельности:

2t 1

tdt

;

4 t

tdt

4 t 2

z 4 t 2 z 2

zdz

z C

4 t 2

C ;

4 t 2

2tdt 2zdz tdt zdz

arcsin

C .

22 t 2

Перейдем в					I1 и I 2
		2x 1			dx

	9 6x 3x			2

	1	arcsin	x 1		C.
	3		2

к переменной		x и окончательно получим
2	2	1	arcsin	x 1	C	2	3 2x x	2
3	4 x 1	3		2		3

Укажем еще			одну			методику			интегрирования	функций,
рационально содержащих				x	2	a	2	.

1) R x,		dx ,	R рациональная
	a2 x2								функция своих	аргументов.

Здесь х может принимать любое вещественное значение; возможна и

удобна подстановка

x atgt

(или x a sht ).

R x,

, здесь

x a ; возможна подстановка

x asin t .

R x,

a2 dx

x a , подстановка

(или x acht ).

sin t

Пример. Найти

5 4x x

dx .

Решение.

5 4x x

x 2

3 sin t

dx 3cos t

d t

3	9 9 sin	2	t cost d t 9 cos	2	t dt	9	1	cos	2 t dt	9		1
3	9 9 sin		t cost d t 9 cos		t dt		1	cos	2 t dt		t
						2				2		2

sin 2		C
sin 2	t	C

Полученный ответ нужно выразить через переменную х:

x 2 3sin t;	sin t	x 2	;	t arcsin	x 2	,

	3			3

				2	x 2	x 2		2	2	x 3
sin 2t 2sin t cost 2sin t	1 sin	2	t	2		x 2			2		5 4x x	2	.
sin 2t 2sin t cost 2sin t	1 sin		t			1					5 4x x		.
				3			3		9

Следовательно,

5 4x x	2	dx	9	arcsin	x 2


			2		3

Упражнение

1)			dx		;
1)		2			;
	x	2	x 6
	x		x 6
4)				dx			;
4)	4x 1 4x					2	;
						2

7)				dx				;
7)	x	2	4x 29					;
		2

10)		4x 3 dx						;
10)		x	2	3x	4			;
			2

4. Найти интегралы:

2)	3x 4 dx											;
2)		x		2			5x					;
				2

	18x							2	13x dx
5)	18x								13x dx						;
		9x					2			6x 1


	x	3						2x		2	4
8)	x							2x			4			dx	;
8)	x		2			2x 3								dx	;
			2

11)									dx					;
11)														;
					2 x x								2
					2 x x

1	x 3	5 4x x					2	C.
	x 3	5 4x x						C.

2
		3)			dx				;
		3)		x	2	2x			;
					2

		6)	x 3 dx						;
		6)		1 4x				2	;
								2

		9)		x	2	4xdx ;
		9)		x		4xdx ;
		12)		1			2x x			2	dx
		12)		1			2x x				dx

	2. Определенный интеграл
Если функция	f x непрерывна на отрезке a,b и если
1) разделить этот	отрезок произвольным способом на	n	частичных

отрезков длиною x1, x2 , x3 ,...,xn ;

2) выбрать в каждом частичном отрезке по одной произвольной точке

c1, c2 ,c3 ,...,cn ;
3)	вычислить значения функции f x в выбранных точках;
4)	составить сумму

n
f c1 x1 f c2 x2 f c3 x3 ... f cn xn f ci xi	,
i 1
то она называется интегральной суммой функции
a,b .

f x

(2.1)

на отрезке

Утверждение. Если последовательность интегральных сумм

	n ( xi 0
вида (2.1) имеет предел при		,	i 1, n ) и этот предел не
зависит от способа разбиения отрезка a,b			на частичные и выбора

точек

( i 1, n ), то он называется определенным интегралом от

f x

b
на a,b ; обозначается f x	dx .
a
По определению:
b				n
f x dx		lim
a		n		i 1
a		x	0	i 1
		i

2.1 Свойства определенного интеграла

Рассмотрим некоторые свойства определенного интеграла.

1. При перестановке пределов интегрирования изменяется знак интеграла:

b	a
f x dx
a	b

x dx

2.Интеграл с одинаковыми пределами равен нулю:

f x dx

3.При любых числах

a, b, c

b	c	b
f x dx f x dx f x dx .
a	a	c

4. Интеграл от алгебраической суммы функций равен такой же сумме интегралов от слагаемых:

b f x g x

b p x dx

b	b
f x dx g x dx
a	a

p x dx

5.Постоянный множитель можно выносить за знак интеграла:

b	b
kf x dx k
a	a

x dx

Вычисление определенного интеграла по определению технически сложно и нецелесообразно. Для вычисления используют следующую формулу.

Утверждение. Если f x dx F x C , то

b	b
f x dx F x	F b F a .
a	a

(2.2) формула Ньютона Лейбница Барроу.

(2.2)

Пример. Вычислить

3		2
	(3x

1)dx

Решение. Применяя формулу Ньютона Лейбница Барроу и свойства 3, 4 определенного интеграла, получим

3	3	3	3	3	(3 2) 20 .
(3x2 1)dx 3 x2dx dx x3			x	33 23	(3 2) 20 .
2	2	2	2	2

Упражнение 5. Вычислить интегралы:

3		x
1) 1 e		3
0

dx ;

	2
2)
	1

	2
x

1
x	4

dx

;

1	dx
3)	dx	;


	4 x2
0	4 x2

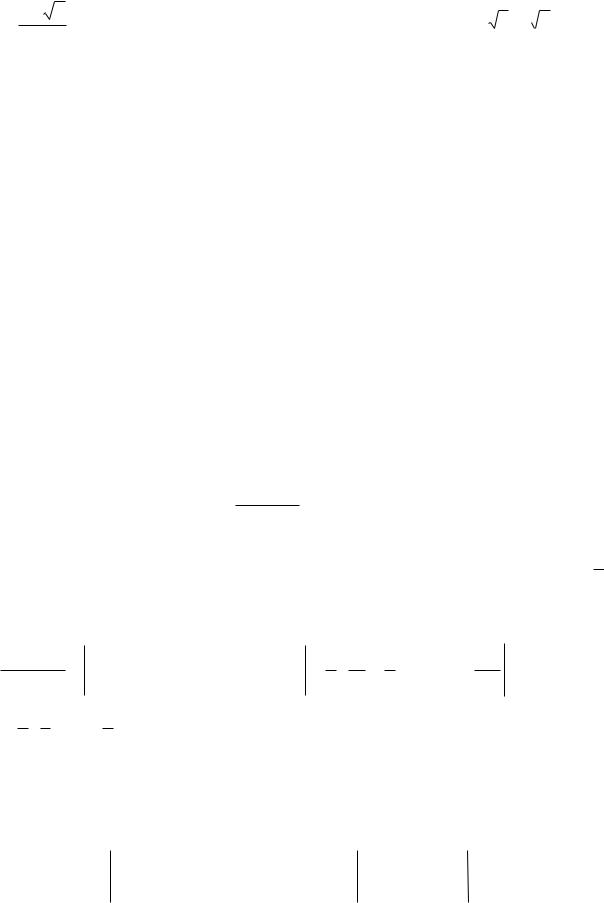
	4
4)
	1

1		x	dx
	2		dx
x	2
x

;

	2	x		2x 3 dx
5)			2
			2

	1

	8
6)
	0

3	x dx

2.2 Замена переменной и интегрирование по частям в

определенном интеграле

I. Замена переменной в определенном интеграле.

Пусть выполняются следующие условия:

1)функция

2)функция отрезке

3)функция

f x непрерывна на отрезке a,b ;

x t непрерывна вместе со своей производной t на , , где a , b ;

f t определена и непрерывна на отрезке , , тогда

b
f x dx
a

t t dt

(2.3)

1	dx
Пример. Вычислить	dx		.
Пример. Вычислить	2x	1	.
0		3
0

Решение. Делаем замену переменной:

находим пределы интегрирования по t: t 1 Удобно вести запись так:

при

1 t, 2dx dt dx

x 0

, t 3

при

12 dt ;

1		dx				2x 1 t 2dx dt
		dx			3	2x 1 t 2dx dt
	2x				3	x	0 t		1; x		1 t		3
0	2x		1			x	0 t		1; x	2	1 t	2	3
0						1		1		2		2
		1		1			2	.
					1			.

		4		9			9
											1
		Пример. Вычислить ex 1 4 exdx
											0
		Решение. Замена переменной e												x
		Решение. Замена переменной e

1	3	dt

2		t	3
	1

t ,

1	3	3		1		3
	t		dt

2				4t	2
	1					1

exdx dt дает

1 4 ex dx e

dx dt

e 1

e 1 5 .

t 4dt

t 5

x1 0 t1 0; x2 1 t2 e 1

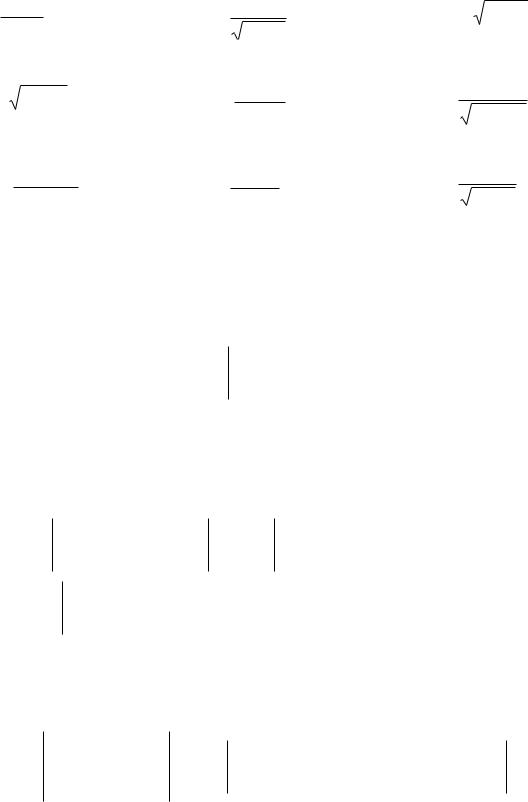
Упражнение 6. Вычислить определенные интегралы:

u u x ,

	2	xdx
1)		xdx						;
1)		1 x				2		;
	1					2


	4				2
4)	x		x		2			9dx ;
4)	x		x					9dx ;
	0
	ln 3						dx
7)							dx			;
7)			e	x			e		x	;
	ln 2			x					x

	1
2)
	0
		e	1
5)

	1
	e	3

8)			x
	e

dx
3x 1
ln x			dx
x

dx		;
	2
ln		x

;

	ln 2		x
3)		e	x	1dx
3)		e		1dx
	0
	2	xdx
6)		xdx			;
6)					;
	0	16 x			2
	0	16 x
	5	xdx
9)		xdx			.
9)		1	3x		.
	1	1	3x
	1

;

II. Интегрирование по частям в определенном интеграле.

Если v v x функции, дифференцируемые на a,b , то

b udv uv

b vdu

(2.4)

1	x
Пример. Вычислить xe	x	dx .
Пример. Вычислить xe		dx .
0
Решение. Полагая, что	u x ,

(2.4), получим

e	x	dx

и применяя формулу

xe x dx u x			du dx			xe x					e x dx e 1		e x dx
1							1					1	1
0	dv e x dx v e x						0					0	0
	1	e 1 e 1 e0 1						2
e 1 e x								2	.
e 1 e x									.
	0							e
					e
	Пример. Вычислить ln xdx .
			1
	Решение. Полагая, что u ln x ,										dv dx , получим
e				dx		e		e				e	e
ln xdx u ln x			du	x	x ln x		x			dx		(eln e ln1) dx e x		e e 1 1.
ln xdx u ln x				x	x ln x		x					(eln e ln1) dx e x		e e 1 1.
1	dv dx		v x			1	1				x	1	1
1						1	1					1	1

	Упражнение 7. Вычислить интегралы:
	2					2
1) x cos xdx ;					2) x ln xdx ;							3) e x cos xdx ;
	0					1							0
							18

	e 1
4)		ln x 1 dx ;

	0

7) x cos xdx ;

		2
5)	x 3 sin xdx
	0
	1
8)	arcsin xdx ;
	0

;

	1
6)	x	2	e		2 x		dx ;
6)	x		e				dx ;
	0
	e
9)	ln			2		xdx .
9)	ln					xdx .
	1

2.3 Вычисление площадей плоских фигур

Площадь S фигуры, ограниченной сверху графиком непрерывной

функции	y f1 x , снизу графиком функции	y	f2 x
( f1 x f2	x x a;b ), слева и справа соответственно прямыми		x a ,
x b , вычисляется по формуле

	b	f	x
S		f	x
		1
	a

f	2	x dx
	2

(2.5)

Пример. Вычислить площадь фигуры, ограниченной графиками

функций	y 4 x	2	и	y x	2	2x .

Решение. Графики функций параболы. Находим абсциссы точек пересечения парабол:

yy




4 x			2	,

x	2	2x.

4 x	2	x	2	2x 2x	2

4 0

x
	1

x2

Тогда по формуле (2.5) получим

2							2				dx
S 4 x2			x2 2x dx 4 2x 2x2								dx
1							1
	2	2		3	2			16				2
4x x			x				8 4		4	1			9(кв.ед).
4x x			x				8 4		4	1			9(кв.ед).
		3				1		3				3
						1

Упражнение 8. Вычислить указанными линиями:

1) y 4x x2 ,

y 0

;

3) y x2 , y 2 x2 ; 5) y 6x , y 7 x ;

площади фигур, ограниченных

2) y x2 4x , y x 4 ;


4) y	2	2x 1, x y 1 0 ;

6) y sin x ,			y 0 , 0 x .

3. Дифференциальные уравнения первого порядка

3.1 Общие понятия

Дифференциальным называется уравнение, содержащее, кроме независимой переменной и неизвестной функции этой переменной, также производные или дифференциалы этой функции.

Наивысший порядок производной неизвестной функции называется порядком дифференциального уравнения.

Примеры.

а)	x	2			2	dy y	2	cos xdx уравнения первого порядка;
а)	x		y 1	xy , sin x 2		dy y		cos xdx уравнения первого порядка;
б)			2xy		0 уравнение второго порядка.
б)	y		2xy		0 уравнение второго порядка.
		Общий вид уравнения n -ого порядка
										n	) 0 .
						F(x, y, y , y ,...,y					) 0 .
			Под		термином	«решение			дифференциального уравнения»

понимают, с одной стороны, результат решения, то есть функции, удовлетворяющие заданному уравнению, а с другой – сам процесс отыскания этих функций, который называют еще интегрированием дифференциального уравнения.


Определение.	Функция	y x	называется			решением
дифференциального	уравнения	на интервале		a,b	,	если при

подстановке в это уравнение самой функции и всех ее производных, указанных в уравнении, получается тождество при любых x a,b .

Особенностью дифференциальных уравнений является то, что каждое из них имеет, как правило, бесконечное множество решений, зависящих в одних случаях от произвольных постоянных, в других и от произвольных постоянных, и от произвольных функций.

Замечание. Дифференциальное уравнение может и не иметь решений (в определенном смысле).

Общий вид уравнения первого порядка:

	0 .	(3.1)
F x, y, y

Нередко уравнение (3.1) разрешимо относительно производной искомой функции:

	f x, y .	(3.2)
y
Функцию f x, y в (3.2)	предполагаем однозначно определенной и

непрерывной в некоторой области D x, y изменения своих аргументов.

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.07.2019397.31 Кб0Метрология.Журнал лабораторных работ.doc
#
03.11.2018971.26 Кб27Метрология.Методичка.doc
#
12.11.20182.24 Mб24Метрология.МИСТ11.doc
#
09.04.2015236.61 Кб28микра.docx
#
09.04.20151.2 Mб28МУ-РГР-Детали машин.pdf
#
09.04.2015796.53 Кб8Наврозов, В. В. Элементы высшей математики 2.pdf
#
31.08.2019628.22 Кб2Новый2.doc
#
26.11.2019336.38 Кб5Нормы - клиника, биохимия, кал.doc
#
09.04.2015460.29 Кб35обработка измерений.doc
#
09.04.201589.6 Кб13Обществознание 2013.doc
#
14.08.2019278.53 Кб3Однородные преобразования.doc