
- •Введение
- •Теоретические сведения
- •Математическая постановка задачи
- •Определение значимости коэффициента корреляции
- •Пример выполнения работы
- •Таблица значений критерия Стьюдента
- •БЛОК-СХЕМА
- •ПРОГРАММА НА ЯЗЫКЕ QBASIC
- •РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ
- •ПРИМЕР РАБОТЫ в EXCEL
- •Контрольные вопросы
- •1. Цель работы.
- •2. Основные теоретические сведения.
- •1). Метод прямоугольников
- •2) Метод трапеций
- •3) Метод парабол
- •3. Порядок выполнения работы
- •Пример выполнения работы
- •БЛОК-СХЕМА
- •ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC
- •РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ В Qbasic
- •Результат расчета в ППП ЭВРИКА.
- •Методические указания к выполнению лабораторной работы на ПК
- •Контрольные вопросы
- •Варианты заданий для самостоятельного решения
- •Задание
- •1. Цель работы
- •2. Основные теоретические положения
- •1). Метод дихотомии
- •2). Метод касательных
- •3). Метод простой итерации
- •4). Метод хорд
- •3. Порядок выполнения работы
- •Пример выполнения лабораторной работы.
- •БЛОК-СХЕМА
- •ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC
- •РЕЗУЛЬТАТЫ РАБОТЫ В QBASIC
- •РЕЗУЛЬТАТЫ РАБОТЫ в Eureka.
- •Варианты заданий для самостоятельного решения
- •Задание.
- •Цель работы
- •Метод Эйлера
- •Метод Эйлера - Коши
- •Метод Руге - Кутта
- •Правило Рунге - Ромберга
- •Пример решения поставленной задачи
- •БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ
- •ВИД ПРОГРАММЫ НА ЯЗЫКЕ QBASIC
- •Построение в Excel графика решений
- •Контрольные вопросы
- •Варианты заданий к лабораторной работе
- •ЛАБОРАТОРНАЯ РАБОТА № 5 Символьные переменные
- •Цель работы
- •Инструменты обработки текстовых величин
- •Базовые алгоритмы обработки текста
- •Сортировка текстовых массивов
- •Контрольные вопросы
- •Варианты заданий для самостоятельного решения
- •Методы оптимизации функции 1-ой переменной
- •Цель работы
- •Оптимизация функций одной переменной
- •Методы оптимизации функций одной переменной
- •Метод поразрядного приближения
- •Метод дихотомии
- •Метод Фибоначчи
- •Метод золотого сечения
- •Использование ППП Eureka и Excel при решении задач оптимизации
- •Содержание отчета
- •Пример выполнения лабораторной работы
- •БЛОК-СХЕМА
- •ПРОГРАММА НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ QBASIC
- •РЕЗУЛЬТАТ в Qbasic
- •Решение задачи с использованием ППП Eureka
- •Задания
- •Контрольные вопросы
- •Цель работы
- •Работа с файлами
- •Требования к имени файла
- •Расширение файла
- •Операции над файлами
- •Порядок выполнения работы
- •Содержание отчета
- •Пример решения задачи
- •ПРОГРАММА НА ЯЗЫКЕ QBasic
- •РЕЗУЛЬТАТ РАБОТЫ ПРОГРАММЫ
- •Контрольные вопросы
- •Варианты заданий к лабораторной работе
- •Список литературы
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,5 |
,6 |
|
7 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
|
1 |
|
2 |
|
3 |
|
4 |
,5 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
, |
, |
, |
, |
|||||||||||
0 |
0 |
0 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
,8 |
|
|
|
|
|
|
,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод Эйлера |
|
|
|
|
|
|
|
|
|
Метод |
Эйлера-Коши |
|
|
|
Метод Рунге-Кутта |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
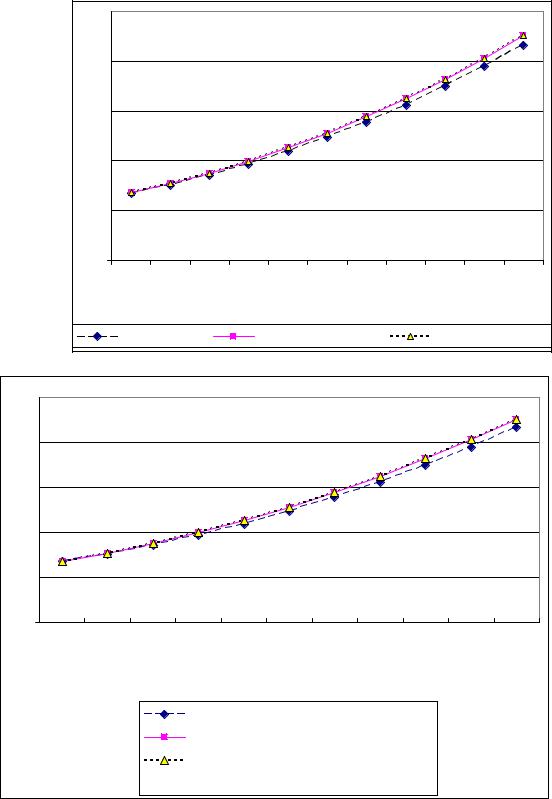
Рисунок 1 |
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
y = 0,6031e0,1176x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
R2 = 0,9995 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
6 |
|
7 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
0, |
, |
, |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
, |
, |
, |
, |
, |
|||||||||
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
, |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод Эйлера |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Метод Эйлера-Коши |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Метод Рунге-Кутта |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Экспоненциальный (Метод Эйлера) |
|
|
|
Рисунок 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы |
|
|
|
|
||||||||||||
Метод Эйлера
1.Что является решением дифференциального уравнения?
2.Необходим ли поиск начальных условий в методе Эйлера?
3.К какой группе относится модифицированный метод Эйлера?
60
4. Почему точность метода Эйлера пропорциональнаh, а модифицированного
— h2?
5.Метод Эйлера относится к одно шаговым методам. В чем основное отличие одно- и многошаговых методов?
6.Можно ли методом Эйлера решать системы дифференциальных уравнений?
7.Можно ли использовать метод Эйлера для решения задач, не относящихся к задачам Коши?
8.Обязательно ли необходимо задание начальных условий при решении дифференциального уравнения методом Эйлера?
9.В чем заключается отличие явных и неявных вычислительных схем модифицированном методе Эйлера?
10.Можно ли оценить погрешность решения дифференциального уравнения, не
зная точного решения?
Метод Рунге — Кутта
1.Сколько раз необходимо на каждом шаге вычислять правую часть уравнения при использовании метода четвертого порядка?
2.Как можно оценить погрешность решения дифференциального уравнения при использовании метода Рунге — Кутта?
3.Можно ли задавать погрешность решения при автоматическом подборе шага в относительных величинах?
4.Сколько предыдущих значений функции нужно иметь, чтобы сосчитать одно следующее значение?
5.К какой группе методов (аналитические или численные) относится имеющий
аналитическое выражение от |
искомого значения |
функции метод Рунге— |
||||
Кутта? |
|
|
|
|
|
|
6. |
Как записывается рекуррентная формула метода четвертого порядка? |
|||||
7. |
Что |
можно |
отнести |
к |
недостаткам , |
напримерметода, самого |
распространенного четвертого порядка?
8.Как зависит погрешность метода от величины шага решения?
9.Возможно ли применение переменного шага в методе Рунге — Кутта?
61
Варианты заданий к лабораторной работе
№ |
Уравнение |
Начальные |
Конечное |
Шаг |
Начальное |
|||||||||||||||||||||||
значение |
||||||||||||||||||||||||||||
п/п |
значение |
значение |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции Y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Y' = y + e2x |
|
|
|
|
|
|
|
|
0 |
1,5 |
0.16 |
Y(0)=3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Y' = cos(x) - y |
0 |
2 |
0.2 |
Y(0)=1.5 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Y' = |
- |
|
12х + 5y - 9 |
|
|
0 |
2 |
0,2 |
Y(0)=0 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
5x + 2y - 3 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Y' = x2 - |
y |
|
|
|
|
|
|
|
|
|
|
1 |
3 |
0,2 |
Y(1)=1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
Y' = e2x - 3y |
|
|
|
|
|
|
|
|
0 |
2 |
0,2 |
Y(0) = 0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Y' = |
|
|
|
|
|
|
1 |
|
|
|
|
- |
|
|
|
|
|
1 |
|
|
0 |
2 |
0,2 |
Y (0) = 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ytg(x) |
||||||||||||||
|
|
|
cos(x) |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7. |
Y' = ex – x + 2y |
0 |
2 |
0,2 |
Y (0) = 0 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
8. |
Y' = |
|
|
|
y |
|
- y 2 |
|
|
|
0 |
2 |
0,2 |
Y (0) = 1 |
||||||||||||||
1+ x |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
9. |
Y' = |
|
y - x2 |
|
|
|
|
|
|
|
|
|
1 |
3 |
0,2 |
Y (1)=1 |
||||||||||||
|
x + x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
10. |
Y' = -4y + sin(2x) |
0 |
1 |
0,2 |
Y(0) = 1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
11. |
Y' = -y + e-xcos(x) |
0 |
2 |
0,1 |
Y(0) = 0 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12. |
Y' = -y + 1-ex |
|
|
|
0 |
2 |
0,2 |
Y(0) = 2,5 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
13. |
Y' = -y + excos(x) |
0 |
1 |
0,2 |
Y(0) = 0 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
14. |
Y' = -y – sin(xex) |
0 |
2 |
0,1 |
Y(0) = 1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
15. |
Y' = xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0,2 |
Y(0) = 1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ y |
ö |
|
|
|
|
|
|
||||||
16. |
Y' = x+ cosç |
|
|
|
|
|
÷ |
|
|
1,7 |
3 |
0,1 |
Y0(1,7) = 5,3 |
|||||||||||||||
|
π |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
17. |
Y' = |
|
|
|
|
x |
+ |
e2 |
|
|
|
1,8 |
2,5 |
0,15 |
Y0(1,3) = 4,5 |
|||||||||||||
2 |
x + y |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
æ x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
18. |
Y' = |
+ |
|
ö |
3 |
|
|
|
|
|
3,1 |
5,4 |
0,1 |
Y0(3) = 5 |
||||||||||||||
ç |
|
|
|
|
|
3y ÷ |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
è 2 |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
19. |
Y' = |
y |
× |
|
|
|
|
y |
|
|
|
|
|
|
|
|
1 |
1,5 |
0,3 |
Y0(1) = О,5 |
||||||||
|
|
lnx -1 |
|
|
|
|||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62
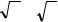
№ |
Уравнение |
Начальные |
Конечное |
Шаг |
Начальное |
||||||||||||
значение |
|||||||||||||||||
п/п |
значение |
значение |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
функции Y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
20. |
Y' = 2x + sin |
y |
|
|
0,1 |
1 |
0,05 |
Y0(0,1)=1 |
|||||||||
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
21. |
Y' = |
x + |
y |
0 |
1 |
0,1 |
Y0(0) = 0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
22. |
Y' = x + (3 + y 2 ) |
|
|
0 |
1 |
0,1 |
Y0(0) = 0 |
||||||||||
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
23. |
Y' = |
|
|
y |
|
|
|
|
|
|
|
0,1 |
1 |
0,1 |
Y0(0,1)=1 |
||
e |
-x |
+ y |
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
24. |
Y' = x-y |
|
|
|
|
|
|
|
|
|
0 |
1 |
0,1 |
Y0(0) = 0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
25. |
Y' = |
|
xy |
|
|
|
|
|
|
|
|
0 |
0,5 |
0,1 |
Y0(0,1)=1 |
||
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
1- x |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
26. |
Y' = 2xy |
|
|
|
|
|
|
|
|
0 |
6 |
0,05 |
Y0(0) = 1 |
||||
|
|
|
|
|
|
||||||||||||
27. |
Y' = 2x – 3y |
0 |
6 |
0,05 |
Y0(0) = 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
63
