
Кол. методы МБА 2012 / 2. Оптимизация / Книжка по ЛП / 4. Анализ опт. реш. 45-58
.pdf4. АНАЛИЗ ОПТИМАЛЬНЫХ РЕШЕНИЙ В ЗАДАЧАХ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
4.1. Необходимость анализа оптимальных решений
Получение оптимального решения в задачах линейного программирования не всегда означает завершение работ по обоснованию и выработке оптимального «поведения». В реальной экономике часто случается так, что изменения во «внешней» среде: колебания спроса, рост инфляции и.т.д., – приводят, например, к необходимости корректировки цен на продукцию. Для оптимизационной модели это означает внесение корректив в целевую функцию. Тут же возникают вопросы: как, и к чему такие коррективы могут привести? Кроме того, обычно существует возможность привлечения для реализации производственной программы дополнительных финансовых и других ресурсов, либо перераспределения уже имеющихся. Вполне естественно попытаться выяснить, к чему это приведет и как скажется на уже полученном оптимальном решении. Иначе говоря, после решения задачи оптимизации в силу разных причин могут возникнуть вполне закономерные вопросы.
•Насколько устойчиво полученное оптимальное решение к изменению параметров модели, в частности, коэффициентов целевой функции? Что произойдет, например, если спрос на продукцию упадет (возрастет) и, следовательно, придется снизить или повысить цену на то или иное изделие? Что в этом случае делать с полученной ранее оптимальной производственной программой? Потребуется ли ее корректировка или нет?
•Насколько чувствительно решение к изменениям запасов ресурсов,
т.е. к изменению правых частей в неравенствах системы ограничений? Изменится ли доходность (значение целевой функции) при изменении запасов и насколько?
•Как оценить вклад единицы каждого из ресурсов в доходность?
Какие ресурсы целесообразно увеличить в первую очередь? К какому результату это может привести? Не являются ли запасы некоторых ресурсов избыточными и вместо затрат на их приобретение и хранение, не лучше ли пополнить запасы тех ресурсов, которые в наибольшей степени увеличивают доходность и расходуются полностью? Как количественно просчитать (оценить) различные вари-
анты «ресурсного» поведения?
Получение ответов на перечисленные вопросы и составляет суще-
ство анализа оптимальных решений.
45
Заметим, что в линейном программировании под устойчивостью обычно подразумевают неизменность оптимальных решений при изменениях (вариациях) коэффициентов целевой функции, а под чувствительностью – степень влияния правых частей ограничений на прирост либо уменьшение значений целевой функции.
С точки зрения обоснования управленческих решений, анализ устойчивости и чувствительности часто играет не менее важную роль, чем отыскание собственно оптимального решения.
4.2. Анализ устойчивости оптимальных решений к изменению коэффициентов целевой функции.
Выясним вначале, как влияет изменение коэффициентов целевой функции на оптимальное решение. Такая проблема возникает в случаях, когда, например, меняется рыночная ситуация, приводящая к колебаниям спроса и, следовательно, к изменению стоимости единицы продукции. Для иллюстрации рассмотрим задачу нахождения оптимальной производственной программы с двумя переменными. С точки зрения модели линейного программирования, это приводит к необходимости изменения коэффициентов c1,c2 целевой функции
(целевых коэффициентов).
Пусть для некоторой исходной целевой функции
Z1 = c1x1 +c2x2 ,
получено оптимальное решение (x1opt, x2opt ) . Выясним, изменится ли
оно при изменении коэффициентов c1,c2 . Для этого рассмотрим два |
|||||||||||||
|
|
|
|
|
случая Z2 = c1 * x1 +c2 * x2 |
||||||||
X2 |
g3 |
={c1 **, c2 **} |
Z |
3 |
= c **x +c |
2 |
**x |
2 |
. |
||||
|
|
1 |
1 |
|
|
|
|||||||
|
|
|
|
|
Заметим, что значение самой |
||||||||
|
|
|
Z3 |
целевой функции Z всегда будет |
|||||||||
|
|
g2 ={c1*, c2 *} |
либо увеличиваться, либо умень- |
||||||||||
|
|
шаться |
|
при |
любом |
изменении |
|||||||
|
|
|
g1 ={c1,c2} |
c1,c2 . Однако важнее выяснить |
|||||||||
|
|
|
другое – измениться ли при этом, |
||||||||||
|
|
Z1 |
Z2 |
ранее |
найденное |
оптимальное |
|||||||
|
|
решение – оптимальные значения |
|||||||||||
|
|
X1 |
|||||||||||
|
|
|
переменных |
(x |
, x |
|
) |
или |
|||||
|
|
|
|
|
|
|
|
1opt |
|
|
2opt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нет.
Рис. 4.1. Иначе говоря, требуется выяснить, достигается ли наибольшее значение новой целевой функции
46
с измененными коэффициентами в той же точке (x1opt, x2opt ) , что и |
|||||||||
ранее, или оптимальное решение будет достигаться при другой ком- |
|||||||||
бинации переменных (x1, x2 ) . |
|
|
|
||||||
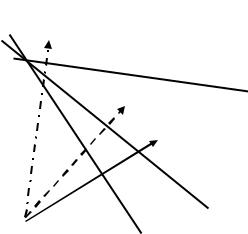
Как было показано в главе 3, коэффициенты целевой функции од- |
|||||||||
нозначно определяют вектор g , указывающий направление возраста- |
|||||||||
ния значений Z. Следовательно, трем рассматриваемым случаям будут |
|||||||||
соответствовать три разных направления роста целевых функций. Ли- |
|||||||||
нии уровня (прямые, во всех точках которых Z=const) всегда перпен- |
|||||||||
дикулярны вектору g . Следовательно, ориентация линий уровня и на- |
|||||||||
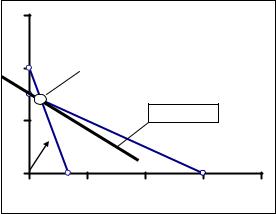
правления возрастания Z для трех случаев будет различным (рис. 4.1.). |
|||||||||
Сопоставим |
этот |
вывод |
с |
Z1 Точка оптимума |
|||||
«поведением» линий уровня в X2 |
|||||||||
ОДР. Заметим, что область до- |
Z2 |
|
|||||||
пустимых решений при измене- |
Z3 |
|
|||||||
нии |
целевых |
коэффициентов |
Б |
|
|||||
остается неизменной. Пусть, на- |
|
||||||||
А |
|
||||||||
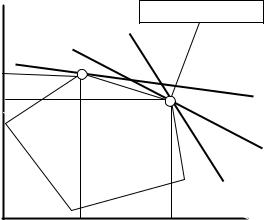
пример, ОДР задачи изображена |
|
||||||||
на рис. 4.2. и пусть оптимальное |
ОДР |
|
|||||||
|
|
||||||||
решение для |
исходной задачи |
|
|
||||||
находится в точке А. Анализируя |
|
X1 |
|||||||
положение |
линий |
уровня |
для |
|
|||||
|
|
||||||||
рассматриваемых |
|
целевых |
|
|
|||||
функций, устанавливаем (рис. |
Рис. 4.2. |
|
|||||||
4.2) следующее. |
|
|
|
|
|
|
|||
1. Для целевой функции Z2 = c1 * x1 +c2 * x2 точка оптимума не |
|||||||||
изменилась и по-прежнему находится в вершине А. Это означает, что |
|||||||||
максимальное значение целевой функции Z2 = c1 * x1 +c2 * x2 |
дос- |
||||||||
тигается в той же оптимальной точке, что и ранее (x1А,x2А) . |
|
||||||||
2. Точка оптимума для целевой |
функции Z3 = c1 **x1 +c2 **x2 |
||||||||
переместилась в точку Б (в другую вершину ОДР). Это означает, что |
|||||||||
теперь максимального значения целевой функции Z3 можно добиться |
|||||||||
только при новой комбинации переменных - (x1Б,x2Б) . |
|
||||||||
Таким образом. |
|
|
|
|
|
|
|||
•Изменение коэффициентов целевой функции в рамках некоторого диапазона не приводит к изменению оптимального решения (x1opt, x2opt ) . Такой диапазон называют диапазоном устойчивости решения по коэффициенту целевой функции.
47
•Границы диапазона устойчивости зависят как от ОДР, так и от целевой функции.
•При изменениях целевых коэффициентов, выходящих за границы диапазона устойчивости, оптимальное решение (x1opt, x2opt ) меняется. Оно перемещается в другую точку ОДР.
При решении задач линейного программирования с большим числом переменных определение границ устойчивости в принципе не составляет труда, однако требует применения довольно громоздких вычислительных процедур [5, 10]. Вместе с тем, эти алгоритмы легко реализуются на ЭВМ. Они включены во многие стандартные пакеты соответствующих программ линейной оптимизации, в том числе и в MS Excel. Все выводы, полученные для задачи с двумя переменными, справедливы и для задач со многими переменными.
4.3. Анализ чувствительности оптимальных решений к изменениям в ограничениях
С содержательной точки зрения, правые части ограничений во многих моделях линейной оптимизации задают уровень запаса того или иного ресурса. Выясним, что происходит с оптимальным решением при изменении запаса какого-либо из ресурсов.
Для иллюстрации воспользуемся результатами примера 3.3 о нахождении оптимальной производственной программы обувной фабрики, в которой требовалось максимизировать целевую функцию
Z =100 x1 +50 x2 .
при условии, что переменные удовлетворяют системе ограничений
7x1 +2x2 ≤ 700,2x1 +4x2 ≤ 480,2x1 +2x2 ≤300,
x1 ≥ 0, x 2 ≥ 0 .
Область допустимых решений, соответствующая данной системе ограничений, показана на рис. 4.3. Оптимальная точка, в которой достигается максимальное значение целевой функции (линия уровня Z=11500), как было выяснено в примере 3.3, расположена в вершине А. Заметим, что она лежит на пересечении граничных прямых, соответствующих первому и третьему ограничениям системы. Уравнения этих прямых 7x1 +2x2 = 700 и 2x1 +2x2 = 300 .
48
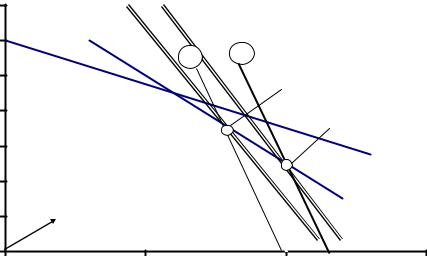
Выясним, к каким изменениям в оптимальном решении приведет, |
||||
например, увеличение ресурса «1» с 700 до 840 единиц при неизмен- |
||||
ности других ограничений. В этом случае уравнение новой граничной |
||||
прямой «1*» примет вид 7x1 +2x2 =840 . Она будет параллельна ис- |
||||
ходной прямой «1», но расположена правее. Соответственно изменит- |
||||
ся и граница ОДР – к ней добавится заштрихованная область. |
|
|||
X2 |
Z=11500 |
Z=13000 |
|
|
140 |
|
|
|
|
120 |
|
1 |
1* |
|
100 |
|
|
||
|
|
A |
|
|
|
|
|
|
|
80 |
|
|
B |
|
60 |
|
|
|
|
ОДР |
|
2 |
|
|
40 |
|
|
||
|
|
3 |
|
|
20 |
g |
|
|
|
|
|
|
||
0 |
|
|
|
X1 |
0 |
|
50 |
100 |
150 |
Рис. 4.3.
Видно, что в этом случае наибольшее (оптимальное) значение целевой функции будет достигаться в новой точке B, поскольку, чем далее линия уровня расположена от начала координат, тем большие значения принимает Z. Следовательно, увеличение данного ресурса привело, во-первых, к новой точке оптимума (новой оптимальной производственной программе), а во-вторых, к увеличению значения целевой функции (дохода). Значит ли это, что если увеличивать запас ресурса «1» до бесконечности, то и доход будет бесконечно прирастать? Оказывается, нет. Иллюстрацией служит рис 4.4. Как только граничные линии 1** ( 7x1 +2x2 =1050 ) и 3 пересекутся с осью OX1 , даль-
нейший прирост ресурса «1» ничего не даст и «в игру» вступят ограничения по другим ресурсам. Легко проверить, что после того, как значение ресурса превысит величину 1050, ОДР не будет изменяться (прирастать) и оптимальная угловая точка С не сможет перемещаться в область дальнейшего роста значений целевой функции. Предельное значение целевой функции в этом случае будет Z=15 000. Следова-
тельно, влияние запаса ресурса на доходность ограничено определенными границами, называемыми границами устойчивости.
49

Таким образом, существует некоторое допустимое увеличение и некоторое допустимое уменьшения запаса ресурсов (правых частей ограничений), в рамках которого, изменяя ресурс, воможно влиять на доходность. При выходе за эти границы увеличение или уменьшение ресурса уже не влияет на доходность. Из разряда дефицитных (расходуемых полностью) такой ресурс переходит в разряд избыточных (недефицитных).
140 |
X2 |
Z=11500 |
Z=15000 |
|
|
|
|
|
|
3 |
|
|
|
||
120 |
2 |
1 |
1* |
1** |
1*** |
|
|
100 |
|
|
|
||||
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
60 |
|
|
A |
|
|
|
|
|
|
|
B |
|
|
|
|
40 |
|
|
|
|
|
|
|
|
ОДР |
|
|
|
|
||
20 |
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
X1 |
|
0 |
50 |
|
100 |
|
150 |
|
|
|
|
200 |
||||
|
Рис. 4.4. |
|
|
Заметим, что если увеличивать ресурс «2», то это не приведет ни к |
|||
изменению точки оптимума (оптимальной производственной про- |
|||
граммы), ни к изменению целевой функции (дохода). Этот ресурс из- |
|||
быточен (не дефицитен) и в принципе его запас можно уменьшать, |
|||
X2 |
Z=11500 |
|
|
140 |
|
|
|
120 |
3 |
|
|
100 |
1 |
|
|
|
A |
|
|
80 |
|
|
|
60 |
|
C |
2 |
40 |
|
||
|
|
|
|
20 |
|
|
2* |
0 |
|
|
X1 |
0 |
50 |
100 |
150 |
|
Рис. 4.5. |
|
|
|
50 |
|
|
используя освободившиеся средства для других целей. Однако сни-
жать запас ресурса «2» без влияния на оптимум можно только до определенного предела. Действительно, при его уменьшении граничная прямая будет перемещаться вниз. Как следует из рис. 4.5., область допустимых решений при уменьшении запаса ресурса 2 будет изменяться (уменьшаться). Причем, как только линия 2 пересечет точку А, все кардинально изменится. Точка оптимума перейдет в новую вершину С – точку пересечения граничных прямых 1 и 2*. При этом оптимальное значение Z станет меньше, чем ранее, а ресурс «3» перейдет в разряд избыточных, не дефицитных.
Таким образом, можно сделать следующие выводы.
•Увеличение (уменьшение) значений целевой функции в зависимости от изменений в правых частях ограничений происходит только в рамках определенного диапазона.
•При выходе за границы такого диапазона изменение правых частей ограничений не приводит к изменениям целевой функции.
•К увеличению либо уменьшению целевой функции приводит изменение запаса только дефицитных ресурсов.
4.4. Двойственность задач линейного программирования
Для количественной оценки вклада каждого из ресурсов в прирост (уменьшение) целевой функции используются специальные приемы. С их помощью определяют, так называемые, теневые (удельные) це-
ны, показывающие, на какую величину изменится целевая функция при увеличении или уменьшении запаса каждого из ресурсов на единицу.
Для знакомства с аналитическими методами, положенными в основу оценки чувствительности оптимальных решений к изменению правых частей ограничений, рассмотрим так называемую двойственную задачу линейного программирования.
Пример 4.1.
Фабрика производит 2 вида химических удобрений А и Б. Для их производства необходимы компоненты 2-х типов, дневной расход которых на 1 тонну каждого из удобрений приведен в табл. 4.1. Рыночная цена 1 тонны удобрений А составляет 3 тысячи рублей, удобрения Б – 2 тысячи рублей. Требуется так спланировать производственную программу (выбрать объемы выпуска А и Б), чтобы доход от реализации был максимальным.
51
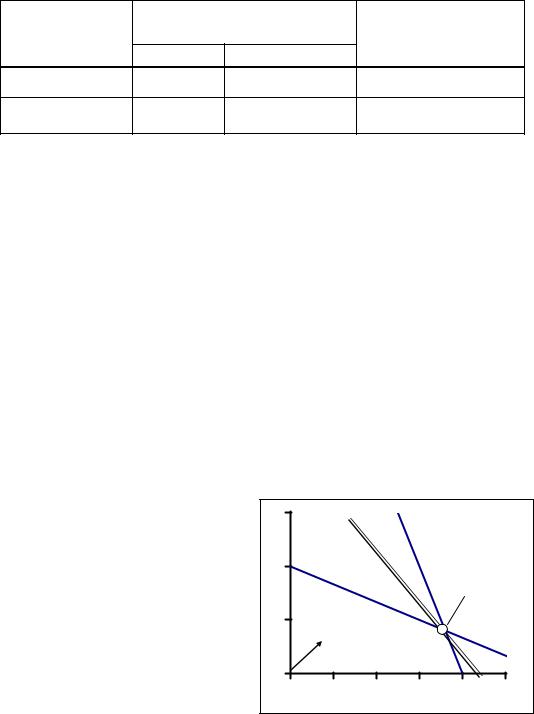
Таблица 4.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ресурс |
|
Расход ресурса |
|
Запасы ресурсов |
|
|||||||
|
на единицу продукции |
|
|||||||||||
|
|
|
|
А |
|
|
Б |
|
|
|
|
|
|
|
№ 1 |
|
|
1 |
|
|
3 |
|
|
|
6 |
|
|
|
№ 2 |
|
|
2 |
|
|
1 |
|
|
|
8 |
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим через x1 объем выпуска (в тоннах) удобрения А, а че- |
|||||||||||||
рез x2 объем выпуска (в тоннах) удобрения Б. Тогда доход от их реа- |
|||||||||||||
лизации будет равен |
Z = 3x1 +2x2 . |
|
|
|
(4.1) |
||||||||
|
|
|
|
|
|
|
|||||||
При этом, исходя из суточных ограничений по запасам исходных |
|||||||||||||
компонентов, должны быть соблюдены ограничения |
|
|
|
||||||||||
|
|
|
|
x1 +3x2 ≤6, |
|
|
|
|
(4.2) |
||||
|
|
|
|
2x |
+x |
2 |
≤8. |
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Кроме того, переменные не отрицательны |
|
|
|
|
|
|
|||||||
|
|
|
|
x1 ≥0 x2 ≥ 0 . |
|
|
|
(4.3) |
|||||
Объединяя все сказанное, приходим к задаче линейного |
|||||||||||||
программирования. Требуется максимизировать целевую функцию |
|||||||||||||
(4.1), если на переменные наложены ограничения (4.2), (4.3). |
|
|
|||||||||||
Решая задачу графоаналитичес- |
3 |
x2 |
Zmax=12,4 |
|
|
|
|
||||||
ким методом (рис.4.6.), находим |
|
|
|
|
|||||||||
|
x1opt =3,6 тонн, |
|
2 |
|
|
|
|
|
|
|
|||
|
x2opt =0,8 тонны. |
|
|
|
|
|
Точка |
|
|||||
При |
такой |
производственной |
|
|
|
|
|
максимума |
|||||
|
|
|
|
|
|
|
|
||||||
программе |
будет |
получен |
1 |
|
ОДР |
|
|
|
|
||||
максимальный доход, а именно: |
|
|
|
|
|
|
|||||||
Zmax =12,4 тысяч рублей. |
|
0 |
|
|
|
|
|
|
x1 |
||||
Рассмотрим |
теперь |
гипоте- |
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|||
тическую ситуацию. Предпо- |
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
ложим, что некто, произ- |
|
|
|
Рис.4.6. |
|
|
|
||||||
водящий аналогичную |
продук- |
|
|
|
|
|
|
|
|
||||
цию, хотел бы устранить фабрику из числа своих конкурентов. |
|||||||||||||
Стоящая перед ним задача заключается в том, чтобы определить – |
|||||||||||||
какую |
цену |
следует |
предложить |
фабрике |
за |
имеющиеся |
у |
нее |
|||||
ресурсы с тем, |
чтобы |
она вообще отказалась от производства, |
т.е. |
||||||||||
|
|
|
|
|
52 |
|
|
|
|
|
|
|
|
чтобы продажа ресурсов была фабрике не менее выгодна, чем производство. Понятно, что следует предложить цену, при которой
доход от продажи ресурсов будет, как минимум, таким же, как и доход, который фабрика сможет достичь при оптимальной производственной программе, запустив эти ресурсы в производство.
Заметим, что такая гипотетическая цена ресурсов никак не связана с их рыночной стоимостью. Речь идет о ценности ресурсов для производителя (фабрики) как источника, приносящего доход.
Для решения обозначим гипотетические цены единицы каждого ресурса через y1, y2 . Тогда, y1 – цена единицы ресурса № 1 (тыс.
рублей за 1 тонну), y2 – цена единицы ресурса № 2 (тыс. рублей за 1
тонну).
Для определения оптимальной цены, обеспечивающей при продаже доход, не меньший чем при производстве, можно сформулировать самостоятельную задачу линейного программирования.
Так как в прямой задаче цена одной тонны продукта А была равна 3 тысячам рублей, то и выручить от продажи ресурсов, затрачиваемых на производство A, нужно не менее, чем 3 тысячи рублей. Поскольку на производство единицы А расходуется одна единица ресурса № 1 и две единицы ресурса № 2 – табл. 4.1, то получаем первое ограничительное условие
y1 + 2y2 ≥ 3.
Рассуждая аналогично, получаем второе ограничительное условие
3y1 + y2 ≥ 2 .
Искомые цены не могут быть отрицательными, поэтому y1 ≥ 0 y2 ≥ 0 .
С позиций гипотетического покупателя-конкурента целевая функция – это суммарная стоимость приобретаемых им ресурсов, которую необходимо минимизировать. Так как запасы ресурсов фабрики 6 и 8 тонн, то их суммарная стоимость при цене за единицу y1, y2 будет равна
Z* = 6y1 +8y2 .
Таким образом, для нахождения оптимальных гипотетических цен на ресурсы необходимо найти минимум целевой функции
Z* = 6y1 +8y2 min . |
(4.4) |
||
При ограничениях |
|
|
|
y +2y |
2 |
≥ 3, |
(4.5) |
1 |
|
||
3y1 + y2 ≥ 2, |
|
||
53
|
|
|
y1 ≥ 0 |
y2 ≥ 0 . |
|
|
(4.6) |
||
Решая эту задачу графоана- |
3 |
y2 |
|
|
|
||||
литическим методом (рис. 4.7.), |
|
|
ОДР |
|
|
||||
находим оптимальные |
гипотети- |
|
|
|
|
||||
ческие цены ресурсов: |
|
|
2 |
Точка минимума |
|
||||
• |
y1opt= 0,2 |
тысячи |
рублей |
за |
|
|
Zmin=12,4 |
|
|
|
тонну ресурса № 1, |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|||
• |
y2opt =1,4 |
тысячи |
рублей |
за |
|
|
|
|
y1 |
|
тонну ресурса № 2. |
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|||
При этом |
|
|
|
0 |
1 |
2 |
3 |
4 |
|
Z *min =12,4 тысячи рублей. |
|
|
|
Рис.4.7. |
|
|
|||
|
Заметим, что оптимальное (минимальное) |
|
|
||||||
значение целевой функции во второй задаче в |
|
|
|
||||||
точности совпало с оптимальным (максимальным) значением целевой |
|||||||||
функции в исходной задаче |
|
|
|
|
|
|
|||
Zmax =12,4 , Z *min =12,4. |
(4.7) |
Полученный результат является крайне важным и ниже будет рассмотрен подробнее.
Найденные y1opt= 0,2 и y2opt =1,4 - это стоимость ресурсов с
точки зрения их ценности для производителя. В теории линейного программирования их называют теневыми ценами (объективно обусловленными оценками, двойственными оценками).
Выясним, как можно использовать теневые цены для анализа оптимальных решений и как использовать равенство оптимальных значений целевых функций (4.7).
Для этого вначале проанализируем особенности рассмотренных выше задач, из которых первую называют исходной (прямой), а вторую двойственной по отношению к первой. Двойственная задача полностью основана на исходных данных прямой задачи и в отрыве от нее не имеет смысла.
Сравним обе задачи примера 4.1 – табл.4.2.
54
