
Кол. методы МБА 2012 / 2. Оптимизация / Книжка по ЛП / 8. Распред.задачи 126-137
.pdf8. МОДЕЛИ И ЗАДАЧИ РАСПРЕДЕЛИТЕЛЬНОГО ТИПА
8.1. Введение
Распределительные задачи, или задачи о назначениях, формулируются следующим образом. Необходимо выполнить n различных работ. Для выполнения работ можно привлечь n исполнителей. Каждый исполнитель может выполнить любую из работ за определенную плату или за определенное время. На каждую работу назначается только один исполнитель. Требуется так распределить работы между исполнителями, чтобы общие денежные затраты или суммарное время, потраченное на выполнение всех работ, были минимальны.
Исходной информацией для постановки и решения задач является таблица, с показателями эффективности назначений – cij . Это могут
быть стоимости работ, время их выполнения, индексы совместимости и другое (табл. 8.1.).
Таблица 8.1.
Исполнители |
|
|
Работа |
|
|
|
1 |
2 |
… |
j |
… |
n |
|
1 |
c11 |
c12 |
… |
c1j |
… |
c1n |
2 |
c21 |
c22 |
… |
c2 j |
… |
c2n |
… |
… |
… |
… |
… |
… |
… |
i |
ci1 |
ci2 |
… |
cij |
… |
cin |
… |
… |
… |
… |
… |
… |
… |
n |
cn1 |
cn2 |
… |
cnj |
… |
cnn |
Решением задачи о назначениях является набор значений переменных xij (табл. 8.2.), принимающих одно из двух значений:
−xij = 1, если i-ый исполнитель назначается на j-ую работу,
−xij = 0, если i-ый исполнитель не назначается на j-ую работу.
Переменные такого типа называют двоичными, булевыми, бинарными или логическими.
126
Таблица 8.2.
Исполнители |
|
|
Работа |
|
|
|
1 |
2 |
… |
j |
… |
n |
|
1 |
x11 |
x12 |
… |
x1j |
… |
x1n |
2 |
x21 |
x22 |
… |
x2 j |
… |
x2n |
… |
… |
… |
… |
… |
… |
… |
i |
xi1 |
xi2 |
… |
xij |
… |
xin |
… |
… |
… |
… |
… |
… |
… |
n |
xn1 |
xn2 |
… |
xnj |
… |
xnn |
В математической записи модель задачи линейного программирования о назначениях имеет вид:
n n
∑∑cij xij min i=1 j=1
n
,n.
i=1 n
∑xij =1, i =1,2,..., n.∑xij =1, j =1,2,...
j=1
xij ≥0, i =1,2,..., n; j =1,2,..., n .
Задача о назначениях является частным случаем транспортной задачи линейного программирования. Возможность применения «транспортных» алгоритмов для решения задач распределительного типа обусловлена тем, что они близки по структуре целевой функции
иограничений. В качестве стоимостей перевозок в них выступают показатели эффективности назначений, количество поставщиков совпадает с количеством потребителей. Особенностью является то, что величины спроса и предложения для каждого поставщика (исполнителя)
ипотребителя (работы) равны единице.
8.2. Задача оптимального распределения бригад по объектам
Ремонтно-строительная фирма получила заказы на ремонт 5 объектов. Для выполнения работ она может привлечь 5 бригад отделочни-
127

ков. Каждая из бригад оценила объемы работ и дала следующие сроки выполнения заказов (человекодней) – табл.8.3
Таблица 8.3.
Бригада |
|
|
Объект |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|||
|
|||||||
|
|
|
|
|
62 |
|
|
Иванова |
43 |
24 |
35 |
|
35 |
||
Петрова |
45 |
21 |
38 |
58 |
33 |
||
Сидорова |
51 |
29 |
36 |
61 |
38 |
||
Волкова |
47 |
27 |
35 |
60 |
39 |
||
Козлова |
48 |
26 |
37 |
59 |
39 |
||
Требуется:
1)распределить объекты между бригадами так, чтобы суммарное количество человекодней, затраченное на ремонт всех 5 объектов, было минимальным;
2)выяснить, сколько человекодней будет затрачено на ремонт всех объектов при оптимальном распределении бригад;
3)установить, какой из объектов следует поручить бригаде Волко-
ва.
Решение
Для решения задачи введем в рассмотрение переменные xij специ-
ального вида, каждая из которых будет принимать только два значения 0 или 1, а именно всякому назначению бригады на объект будет соответствовать единица, в противном случае – ноль.
1, если i −ая бригада назначается на j −ый объект; xij = 0 впротивномслучае.
Тогда искомый план назначений будет содержать 25 значений переменных (табл. 8.4.).
Причем, каждый столбец табл. 8.4 должен содержать только одну единицу и остальные нули, так как объект может обслуживаться только одной бригадой.
Аналогичный вывод справедлив и для строк – в каждой из них может содержаться только одна единица, а остальные элементы будут нулями. Это обусловлено тем, что каждой бригаде выделяется только один объект.
128

Формально задача о назначениях совпадает с транспортной моделью. При этом в качестве «стоимостей перевозок» cij в ней выступает
время (человекодни), а в качестве «объема перевозимого груза» xij –
количество бригад, назначаемых на объект (либо ноль, либо единица). По аналогии с транспортной моделью можно считать, что «запас» каждой бригады состоит из количества объектов, которые ей выделяются для работы. Понятно, что такой запас для каждой бригады будет равен единице. «Заявкой» для каждого объекта является количество бригад, которые его ремонтируют. Они также равны единице для каждого из объектов – табл. 8.4.
Таблица 8.4.
Бригада |
|
|
Объект |
|
|
«Запасы» |
|
1 |
2 |
3 |
4 |
5 |
|||
|
|
||||||
Иванова |
x11 |
x12 |
x13 |
x14 |
x15 |
1 |
|
Петрова |
x21 |
x22 |
x23 |
x24 |
x25 |
1 |
|
Сидорова |
x31 |
x32 |
x33 |
x34 |
x35 |
1 |
|
Волкова |
x41 |
x42 |
x43 |
x44 |
x45 |
1 |
|
Козлова |
x51 |
x52 |
x53 |
x54 |
x55 |
1 |
|
«Заявки» |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
С учетом особенностей введенных переменных (ноль или единица) целевая функция - суммарное количество человекодней, затраченное на ремонт всех объектов, можно вычислить по формуле
Z = 43 x11 +24 x12 +35 x13 +62 x14 +35 x15 +
+45 x21 +21 x22 |
+38 x23 +58 x24 |
+33 x25 |
+ |
(8.1) |
+ |
|
+ |
||
.............................. |
|
|||
+48 x51 +26 x52 +37 x53 +59 x54 +39 x55.
Ограничения, связанные с тем, что каждая из бригад может ремонтировать только один объект, математически можно записать следующим образом («баланс запасов»)
129
x11 +x12 +x13 +x14 +x15 =1, |
|
||
|
+x22 |
+x23 +x24 +x25 =1, |
|
x21 |
(8.2) |
||
|
|
|
|
M |
|
|
|
|
+x52 |
+x53 +x54 +x55 =1. |
|
x51 |
|
||
Ограничения, связанные с тем, что за каждым объектом закрепляется только одна бригада, можно записать следующим образом («баланс заявок»)
x11 +x |
21 +x31 +x41 +x51 =1, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
x12 +x22 +x32 +x42 +x52 =1, |
(8.3) |
||||||||
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
x +x |
25 |
+x |
35 |
+x |
45 |
+x |
55 |
=1. |
|
15 |
|
|
|
|
|
||||
Все искомые переменные неотрицательны |
|
|
|||||||
xij ≥0, |
i =1,2,...,5; |
j =1,2,...,5. |
(8.4) |
||||||
Таким образом, исходная задача о назначениях полностью соответствует транспортной модели замкнутого типа – необходимо минимизировать целевую функцию (8.1) при условии, что на переменные наложены ограничения (8.2) – (8.4).
В задаче о назначениях, также как и в замкнутой транспортной модели,
•число поставщиков (бригад) равно числу потребителей (объектов);
•выполнено условие баланса (запас равен заявкам);
•все ограничения записаны в виде равенств;
•коэффициенты при неизвестных в системе ограничений равны
единице.
Для решения задач распределительного типа, к числу которых относится и рассматриваемая, целесообразно использовать транспортные алгоритмы. Поиск решения в Excel автоматически «распознаёт» такие задачи и использует для решения соответствующие вычислительные алгоритмы, которые значительно более эффективны, чем симплекс метод. Это обстоятельство играет важную роль, особенно для задач большой размерности.
Важной особенностью, отличающей распределительные задачи от транспортных, является двоичность искомых переменных. Они могут принимать только два значения: ноль или единицу. Однако задавать
130
это условие в виде отдельного ограничения не требуется. В теории линейного программирования доказано [4, 5, 10], что в силу особенностей системы ограничений таких задач, при целочисленности правых частей ограничений (у нас они равны единице), все искомые переменные xij «автоматически» будут иметь «двоичную» природу, т.е.
окажутся равными нулю или единице.
Решение задачи в Excel показано на рис. 8.1 – 8.3.
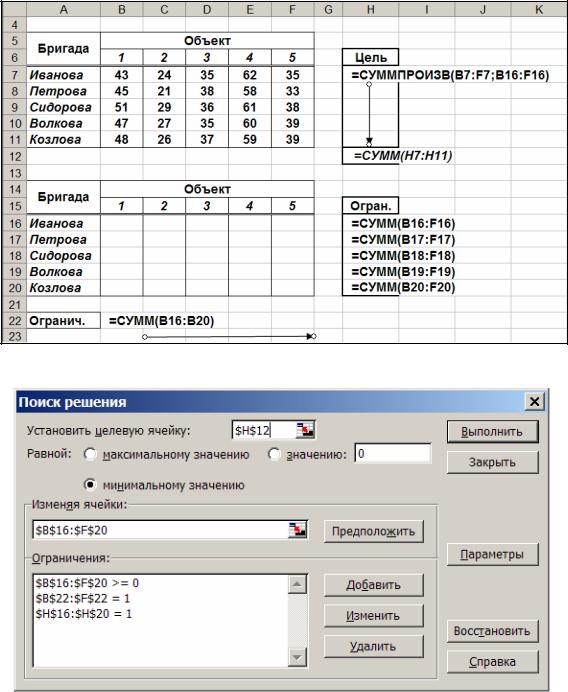
Рис. 8.1. Табличное представление модели в Excel.
Рис. 8.2. Окно «Поиска решения»
131
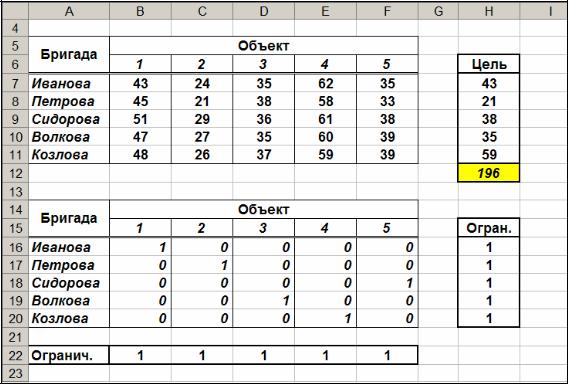
Рис. 8.3. Найденный «Поиском решения» оптимальный план назначений.
Ответы
1. Оптимальное распределение бригад по объектам приведено в табл. 8.5.
Таблица 8.5.
Бригада |
|
|
Объект |
|
|
|
1 |
2 |
3 |
4 |
5 |
||
|
||||||
|
|
|
|
|
|
|
Иванова |
1 |
|
|
|
|
|
Петрова |
|
1 |
|
|
|
|
Сидорова |
|
|
|
|
1 |
|
Волкова |
|
|
1 |
|
|
|
Козлова |
|
|
|
1 |
|
2.При оптимальном распределении бригад для ремонта всех объектов потребуется 196 человекодней.
3.Бригаде Волкова следует поручить объект № 3.
132

8.3. Задача оптимального распределения рабочих по операциям
Мастер цеха должен назначить на сборку изделия, требующую выполнения шести различных операций, шесть рабочих. В силу разной квалификации рабочие затрачивают на выполнение операций различное время. Результаты их тестирования приведены в табл. 8.6. Следует также учесть, что рабочие 3, 4 не умеют выполнять операцию № 2, а рабочий 6 не может выполнять операцию № 6.
Каким образом оптимально распределить рабочих по операциям, чтобы суммарное время, затрачиваемое на сборку изделия, было минимальным?
Таблица 8.6.
Рабочие |
|
|
Операции |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
23 |
6 |
7 |
12 |
6 |
12 |
2 |
8 |
16 |
11 |
6 |
12 |
11 |
3 |
6 |
|
9 |
8 |
16 |
23 |
4 |
11 |
|
18 |
15 |
15 |
12 |
5 |
12 |
17 |
12 |
11 |
7 |
15 |
6 |
4 |
12 |
11 |
8 |
17 |
|
Решение
Обозначим через cij время (минут), которое i-ый рабочий затрачи-
вает на выполнение j-ой операции (табл. 8.6). Учесть невозможность выполнения операций рабочими 3,4,6 можно, придав неразумно большие значения времени выполнения соответствующих операций, например, положив c32 , c42 , c66 , равными 100. Такой прием заведо-
мо исключает назначение рабочих на эти операции ввиду нецелесообразности из-за больших временных затрат.
Введем в рассмотрение переменные xij , каждая из которых при-
нимает только два значения 0 или 1, а именно:
1, если i −ый рабочий назначается на j −юоперацию; xij = 0 впротивномслучае.
Тогда всякому назначению рабочего на операцию будет соответствовать единица, в противном случае – ноль.
133
Искомое решение задачи о назначениях – это набор из 36 значений для переменных (табл. 8.7.), каждая из которых должна быть равна либо нулю, либо единице.
Таблица 8.7.
Рабочие |
|
|
Операции |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
x11 |
x12 |
x13 |
x14 |
x15 |
x16 |
2 |
x21 |
x22 |
x23 |
x24 |
x25 |
x26 |
3 |
x31 |
x32 |
x33 |
x34 |
x35 |
x36 |
4 |
x41 |
x42 |
x43 |
x44 |
x45 |
x46 |
5 |
x51 |
x52 |
x53 |
x54 |
x55 |
x56 |
6 |
x61 |
x62 |
x63 |
x64 |
x65 |
x66 |
Подсчитаем суммарное время, которое будет потрачено на выполнение всех работ
Z = 23 x11 +6 x12 +... +6 x15 +12 x16 + |
|
|
|
+8 x21 +16 x22 +... +12 x25 +11 x26 |
+ |
(8.5) |
|
+ |
+ |
||
|
+4 x61 +12 x62 +... +17 x65 +100 x66.
Вкаждой строке табл. 8.7. может находиться не более одного назначения. Поэтому сумма переменных xij для каждой i-ой строки
также должна быть равной 1
x11 +x12 +... +x15 +x16 =1, |
|
|||
|
+x22 |
+... +x25 +x26 |
=1, |
|
x21 |
(8.6) |
|||
M |
|
|
|
|
|
|
|
|
|
|
+x62 |
+... +x65 +x65 |
=1. |
|
x61 |
|
|||
Каждую операцию обязательно нужно выполнить, но назначать на нее более одного рабочего нельзя. Следовательно, каждый столбец будет содержать только одну единицу и остальные нули. Поэтом сумма xij для каждого j-го столбца табл. 8.7. также должна быть равна 1,
следовательно
134
x11 +x |
21 +... +x51 +x61 =1, |
|
||||||
|
+x22 |
+... +x52 |
+x62 |
=1, |
|
|||
x12 |
(8.7) |
|||||||
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+x |
26 |
+... +x |
56 |
+x |
66 |
=1. |
|
16 |
|
|
|
|
|
|||
Все искомые переменные неотрицательны |
|
|
||||||
xij ≥0, |
i =1,2,...,6; |
j =1,2,...,6 . |
(8.8) |
|||||
В итоге исходная задача о назначениях также сведена к транспортной модели замкнутого типа – необходимо минимизировать целевую функцию (8.5) при условии, что на переменные наложены ограниче-
ния (8.6) – (8.8).
Решение задачи в Excel показано на рис. 8.4 – 8.6.
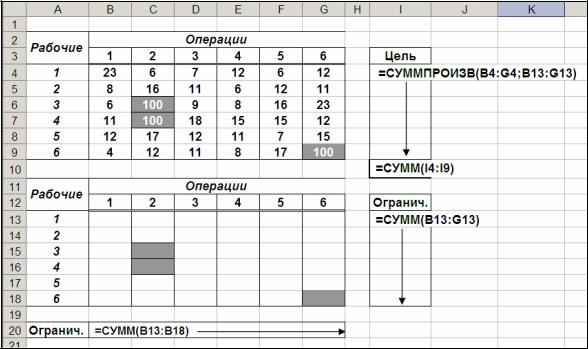
Рис. 8.4. Табличное представление модели (8.5)-(8.8) в Excel.
135
