1) Приведение квадратичных форм к каноническому виду

            Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂

y₂ = a₁₂x₁ + a₂₂x₂

где у₁ и у₂ – координаты вектора  в базисе .

            Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁ + х₂у₂.

 

            Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁ и х₂ – скалярное произведение .

            Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

            Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

            При переходе к новому базису от переменных х₁ и х₂ мы переходим к переменным  и . Тогда: 

            Выражение  называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

2) Полярная система координат на плоскости — это совокупность точки , называемойполюсом, и полупрямой , называемойполярной осью. Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор , приложенный к точке, длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).

Положение точки в полярной системе координат определяется расстоянием(полярным радиусом) от точки до полюса (т.е.)и углом(полярным углом) между полярной осью и вектором . Полярный радиус и полярный угол составляютполярные координаты точки , что записывается в виде. Полярный угол измеряется в радианах и отсчитывается от полярной оси:

- в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;

- в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный уголопределен для любой точки плоскости, за исключением полюса, и принимает значения, называемымиглавными значениями полярного угла. В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых , где. В этом случае значениямполярного угла для всехсоответствует одно и то же направление радиус-вектора.

С полярной системой координат можно связать прямоугольную систему координат, началокоторой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат {связанную с данной прямоугольной).

Выведем формулы, связывающие между собой прямоугольные координаты точки, отличной от точки, и ее полярные координаты. По рис.2.28,б получаем

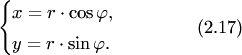
Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:

Последние два равенства определяют полярный угол с точностью до слагаемых , где. Прииз них следует, что. Главное значение полярного угланаходится по формулам (рис.2.29):