- •2) Различные виды уравнения прямой на плоскости
- •Фокальное свойство эллипса
- •Директориальное свойство эллипса
- •Свойства ранга матрицы
- •Директориальное свойство параболы
- •Фундаментальная система решений однородной слу: определение, теорема.
- •2.8. Собственные векторы
- •2. Двуполостный гиперболоид.
- •Определения. Матрица квадратичной формы. Преобразование квадратичной формы к новым переменным.
- •2) Параболоиды.
- •1) Приведение квадратичных форм к каноническому виду
2.8. Собственные векторы
У матрицы A, размерностью (N×N) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора vn нужно решить систему однородных уравнений
(A − λnI) vn = 0.
Она имеет нетривиальное решение, поскольку det(A − λnI) = 0.
Например,

Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.
Собственные значения и собственные векторы линейного преобразования.
Определение: Пусть L –
заданное n-
мерное линейное пространство. Ненулевой
вектор ![]() L называется собственным
вектором линейного
преобразования А, если существует такое
число l, что выполняется равенство:
L называется собственным
вектором линейного
преобразования А, если существует такое
число l, что выполняется равенство:
A![]() .
.
При
этом число l называется собственным
значением (характеристическим
числом) линейного
преобразования А, соответствующего
вектору ![]() .
.
Определение: Если
линейное преобразование А в некотором
базисе ![]() ,
,![]() ,…,
,…,![]() имеет
матрицу А =
имеет
матрицу А = ,
то собственные значения линейного
преобразования А можно найти как
корни l1, l2,
… ,ln уравнения:
,
то собственные значения линейного
преобразования А можно найти как
корни l1, l2,
… ,ln уравнения:
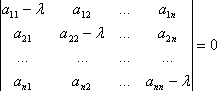
2) Взаимное расположение прямой и плоскости в пространстве.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.

рис.6.
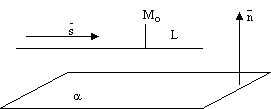
рис.7.
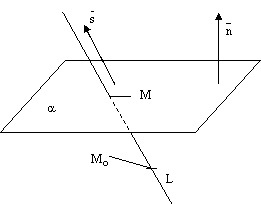
рис.8.
Теорема.
Пусть плоскость ![]() задана
общим уравнением
задана
общим уравнением
![]() ,
,
а прямая L задана каноническими уравнениями
![]()
или параметрическими уравнениями
 ,
, ![]() ,
,
в
которых ![]() – координаты нормального вектора плоскости
– координаты нормального вектора плоскости ![]() ,
, ![]() – координаты произвольной
фиксированной точки прямой L,
– координаты произвольной
фиксированной точки прямой L, ![]() –
–
координаты направляющего вектора прямой L. Тогда:
1)
если ![]() ,
то прямая L пересекает плоскость
,
то прямая L пересекает плоскость ![]() в
точке,координаты которой
в
точке,координаты которой ![]() можно
найти из системы уравнений
можно
найти из системы уравнений
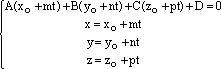 ;
(7)
;
(7)
2)
если ![]() и
и ![]() ,
то прямая лежит на плоскости;
,
то прямая лежит на плоскости;
3)
если ![]() и
и ![]() ,
то прямая параллельна плоскости.
,
то прямая параллельна плоскости.
Доказательство.
Условие ![]() говорит
о том, что вектроры
говорит
о том, что вектроры ![]() и
и ![]() не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
Если ![]() ,
то это означает, что
,
то это означает, что ![]() .
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка ![]() .
Если
.
Если ![]() ,
то точка
,
то точка ![]() –
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
–
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
Если ![]() ,
а
,
а ![]() ,
то точка на прямой не лежит на плоскости,
а это означает, что прямая параллельна
плоскости.
,
то точка на прямой не лежит на плоскости,
а это означает, что прямая параллельна
плоскости.
Теорема доказана.
Билет 21
1)Линейное
пространство ![]() называетсяевклидовым,
если в этом пространстве определена
операция, ставящая в соответствие паре
векторов
называетсяевклидовым,
если в этом пространстве определена
операция, ставящая в соответствие паре
векторов ![]() и
и![]() вещественное
число, называемоескалярным
произведением векторов
вещественное
число, называемоескалярным
произведением векторов ![]() и
и![]() ,
и обозначаемое
,
и обозначаемое![]() ;
при этом операция подчиняется аксиомам:
;
при этом операция подчиняется аксиомам:
1. ![]() для
для![]() ;2.
;2. ![]() для
для![]() ;3.
;3. ![]() для
для![]() ;4.
;4. ![]() для
для![]() ,
,![]() .
.
Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:
2'. ![]() для
для![]() .
.
Примеры евклидовых пространств:
1) Множество всех векторов плоскости или трёхмерного пространства элементарной евклидовой геометрии с обычным скалярным произведением.
2) Конечномерное векторное пространство над R, в котором скалярное произведение векторов x = (x1, x2, ..., xn) и y = (y1, y2, ..., yn) определено формулой (x, y) = x1y1 + x2y2 + ... + xnyn (евклидово n-мерное арифметическое пространство).
2) Эллипсоид, у которого все три полуоси равны, называют сферой.
Каноническое уравнение сферы принято записывать в виде
x2 + y2 + z2 = r2,
где r – величина полуосей, которая называется радиусом сферы.
С геометрической точки зрения, сфера – геометрическое место точек пространства, равноудаленных (на расстояние r) от некоторой фиксированной точки (называемой центром). В канонической системе координат сферы, центр – начало координат.
Билет 22
1) Ортогона́льность — понятие, являющееся обобщением перпендикулярности для линейных пространств с введённым скалярным произведением.
Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу.
Важной особенностью понятия является его привязка к конкретному используемому скалярному произведению: при смене произведения ортогональные элементы могут стать неортогональными, и наоборот. Алгоритм построения для данной линейно независимой системы векторов (в евклидовом или эрмитовом пространстве V) ортогональной системы векторов, порождающих то же самое подпространство в V. Наиболее известным является процесс Грама-Шмидта.
Определение 1. Линейное
пространство конечной размерности над
полем ![]() называется
унитарным, если для любых двух элементов
определена комплекснозначная функция
(скалярное произведение), обозначающаяся
называется
унитарным, если для любых двух элементов
определена комплекснозначная функция
(скалярное произведение), обозначающаяся![]() ,
удовлетворяющая свойствам:
,
удовлетворяющая свойствам:
(Коммутативность)
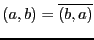 ;
;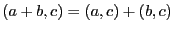 ;
;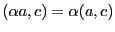 ;
;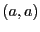 --
вещественное
--
вещественное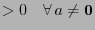 .
.
Определение
евклидова пространства отличается тем,
что поле ![]() заменяется
на
заменяется
на![]() ,
а комплексное сопряжение в свойстве
,
а комплексное сопряжение в свойстве![]() не
требуется.
не
требуется.
Теорема 1. (Грама--Шмидта) в любом конечномерном унитарном (евклидовом) пространстве можно построить ортонормированный базис.
Доказательство. Докажем методом математической индукции.
![]() База
индукции.
База
индукции. ![]() .
.![]() .
Это и есть ОНБ.
.
Это и есть ОНБ.
![]() Предположение.
Пусть верно для
Предположение.
Пусть верно для ![]() .
.
![]() Доказательство
индукции. Возьмем базис
Доказательство
индукции. Возьмем базис ![]() .
Рассмотрим его в
.
Рассмотрим его в![]() -мерном
пространстве
-мерном
пространстве![]() .
По предположению, там найдется ОНБ
.
По предположению, там найдется ОНБ![]() .
Дополним этот базис до базиса
.
Дополним этот базис до базиса![]() :
:![]() (без
ограничения общности, последний вектор
линейно не зависит от этого базиса).
Сконструируем вектор
(без
ограничения общности, последний вектор
линейно не зависит от этого базиса).
Сконструируем вектор
![]()
Нужно, чтобы он был ортогонален всем векторам:
![]()
а
это выполнено тогда и только тогда,
когда (умножая обе части
равенства ![]() на
на![]() последовательно)
последовательно)
![]()
Отсюда, ![]() ,
,![]() .
Теперь положим
.
Теперь положим![]() ,
построив тем самым ОНБ
,
построив тем самым ОНБ![]() и
доказав утрверждение теоремы.
и
доказав утрверждение теоремы.![]()
2)
|
Определение Пр.2.2.1. |
Поверхность, задаваемая в некоторой ортонормированной системе координат каноническим уравнением вида
|
Свойства эллипсоида:
1.
Эллипсоид - ограниченная поверхность,
поскольку из его канонического уравнения
следует, что
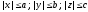 .
.
2. Эллипсоид обладает:
- центральной симметрией относительно начала координат;
- осевой симметрией относительно координатных осей;
- плоскостной симметрией относительно координатных плоскостей.

3. В
сечении эллипсоида плоскостью,
ортогональной любой из осей координат,
получается эллипс.
Например, рассматривая секущую
плоскость
являющейся эллипсом |
x |
z Рисунок Пр.2.2.1.
|
y |
Билет 23
1)
Линейное
пространство ![]() называется евклидовым,
если каждой паре векторов
называется евклидовым,
если каждой паре векторов ![]() ,
, ![]() из
этого пространства поставлено в
соответствие действительное число
из
этого пространства поставлено в
соответствие действительное число ![]() ,
называемое скалярным
произведением,
и при этом для любых
,
называемое скалярным
произведением,
и при этом для любых ![]() из
из ![]() и
любого действительного числа
и
любого действительного числа ![]() справедливы
следующие равенства:
справедливы
следующие равенства:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() при
при ![]() ,
, ![]() ,
, ![]() --
нулевой вектор.
--
нулевой вектор.
Число ![]() называется длиной вектора
называется длиной вектора ![]() ; число
; число ![]() -- расстоянием между
векторами
-- расстоянием между
векторами ![]() ;
угол
;
угол ![]() , косинус
которого
, косинус
которого ![]() ,
-- углом между
векторами
,
-- углом между
векторами ![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
Векторы ![]() ,
,![]() из
евклидова пространства
из
евклидова пространства ![]() называются ортогональными,
если
называются ортогональными,
если ![]() .
.
Система
векторов ![]() евклидова
пространства называется ортонормированной,
если векторы системы попарно ортогональны
и имеют единичную длину.
евклидова
пространства называется ортонормированной,
если векторы системы попарно ортогональны
и имеют единичную длину.
Базис
конечномерного евклидова пространства
называется ортонормированным базисом,
если образующие его векторы попарно
ортогональны и имеют единичную длину.
Поскольку доказано, что в
любом конечномерном евклидовом
пространстве существует ортонормированный
базис,
будем рассматривать в ![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве ![]() только
ортонормированные базисы.
только
ортонормированные базисы.
Простейший
пример евклидова пространства дает нам
пространство ![]() --
пространство столбцов, в котором
скалярное произведение введено
формулой
--
пространство столбцов, в котором
скалярное произведение введено
формулой 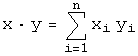 .
.
Тогда
для любых ![]() ,
, ![]() из
из ![]() справедливы
формулы:
справедливы
формулы:
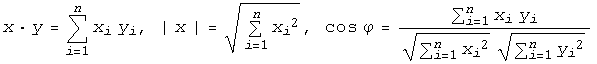
Все
евклидовы пространства размерности ![]() устроены
так же, как пространство
устроены
так же, как пространство ![]() .
.
Величины ![]() ,
, ![]() и
и ![]() характеризуют
взаимное расположение векторов и не
зависят от выбранного ортонормированного
базиса.
Если
характеризуют
взаимное расположение векторов и не
зависят от выбранного ортонормированного
базиса.
Если ![]() и
и ![]() --
два ортонормированных базиса в
--
два ортонормированных базиса в ![]() -мерном
евклидовом пространстве, то матрица
перехода от одного из этих базисов к
другому -- ортогональная матрица.
-мерном
евклидовом пространстве, то матрица
перехода от одного из этих базисов к
другому -- ортогональная матрица.
2) 1. Однополостный гиперболоид. Обратимся к каноническому уравнению (4) однополостного гиперболоида
![]()
Из уравнения (4) вытекает, что координатные плоскости являются плоскостями симметрии, а начало координат — центром симметрии однополостного гиперболоида.

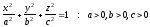 ,
называется эллипсоидом.
,
называется эллипсоидом.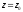 ,
где
,
где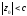 ,
получаем следующее уравнение линии
сечения
,
получаем следующее уравнение линии
сечения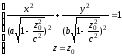 ,
, z
z