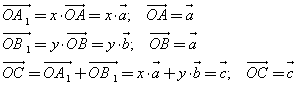- •2) Различные виды уравнения прямой на плоскости
- •Фокальное свойство эллипса
- •Директориальное свойство эллипса
- •Свойства ранга матрицы
- •Директориальное свойство параболы
- •Фундаментальная система решений однородной слу: определение, теорема.
- •2.8. Собственные векторы
- •2. Двуполостный гиперболоид.
- •Определения. Матрица квадратичной формы. Преобразование квадратичной формы к новым переменным.
- •2) Параболоиды.
- •1) Приведение квадратичных форм к каноническому виду
Билет 1
1) Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
2)Знакоопределенные квадратичные формы.
Определение. Квадратичную
форму k будем
называть положительно
определенной на
пространстве ![]() пространства
пространства![]() ,
если
,
если![]() для
любого ненулевого вектораx из
для
любого ненулевого вектораx из ![]() .
Формаk отрицательно
определена на
.
Формаk отрицательно
определена на ![]() ,
если
,
если![]() для
любого
для
любого![]() из
из![]() .
.
Если
говорят, что квадратичная форма
положительно или отрицательно определена,
без уточнения подпространства, то она
обладает таким свойством на всем ![]() .
.
Квадратичные
формы, для которых ![]() или
или![]() при
любомx, называются
соответственно положительно или
отрицательно полуопределенными.
при
любомx, называются
соответственно положительно или
отрицательно полуопределенными.
Удобно считать, что на нулевом подпространстве каждая квадратичная форма положительно определена, и отрицательно определена одновременно. В силу этого соглашения всегда существует (хотя бы нулевое) подпространство, на котором квадратичная форма отрицательно определена.
Билет 2
1)ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ, ДЕТЕРМИНАНТ [determinant] — число, соответствующее квадратной матрице и полученное путем ее преобразования по определенному правилу. Обычное обозначение (для матрицы A): det A.Напр., определитель (второго порядка) матрицы

обозначается

и вычисляется следующим образом:
det A = a11a22 — a12a21.
СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
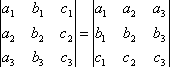 .
.
СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,
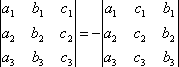 .
.
СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,
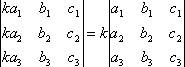 .
.
СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,
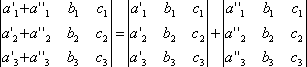
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
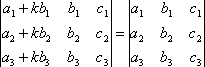 .
.
Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора. Минором некоторого элемента называется определитель, получаемый из данного путем вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца, на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
Алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, кторой обозначен сам элемент.
СВОЙСТВО 9. Определитель
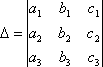
равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
Иначе говоря, имеют место следующие равенства:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
2) Существует ортогональное преобразование n-мерного евклидова пространства, приводящее квадратичную форму к каноническому виду.
Алгоритм приведения квадратичной формы к каноническому виду состоит в слуедующем:
находим собственные значения матрицы квадратичной формы и записываем её канонический вид в виде суммы квадратов, коэффициентами при которых являются собственные значения матрицы;
если нужно указать вид преобразования, то находим собственные векторы матрицы, нормруем их, и записываем матрицу перехода от исходного ортонормированного базиса к базису, составленному из найденных собственных векторов.
Билет 3
1)
Минором ![]() элемента
элемента![]() матрицы
n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы
А вычеркиванием
i-й
строки и j-го
столбца.
матрицы
n-го
порядка называется определитель матрицы
(n-1)-го
порядка, полученный из матрицы
А вычеркиванием
i-й
строки и j-го
столбца.

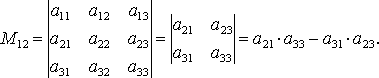
При выписывании определителя (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:
![]()
то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.
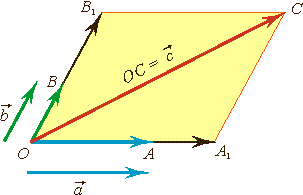
2) Вектором называется направленный отрезок. Если начало вектора находится в точке А, а конец – в точке В, то вектор обозначается АВ. Если же начало и конец вектора не указываются, то его обозначают строчной буквой латинского алфавита a, b, c ,…. Через BA обозначают вектор, направленный противоположно вектору АВ. Вектор, у которого начало и конец совпадают, называется нулевым и обозначается ō. Его направление является неопределенным.Длиной или модулем вектора называется расстояние между его началом и концом. Записи |АВ| и |a| обозначают модули векторов АВ и a.
Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
Сложение
векторов. Пусть ![]() и
и![]() –
два произвольных вектора. Возьмем
произвольную точкуО и
построим вектор
–
два произвольных вектора. Возьмем
произвольную точкуО и
построим вектор ![]() ;
затем от точкиА отложим
вектор
;
затем от точкиА отложим
вектор ![]() .
Вектор
.
Вектор![]() ,
соединяющий начало первого слагаемого
вектора с концом второго, называетсясуммой этих
векторов и обозначается
,
соединяющий начало первого слагаемого
вектора с концом второго, называетсясуммой этих
векторов и обозначается ![]() (рис.
1).
(рис.
1).
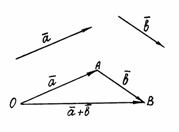
Рис. 1
Ту
же сумму можно получить иным способом.
Отложим от точки О векторы ![]() и
и![]() .
Построим на этих векторах как на сторонах
параллелограммОАСВ.
Вектор
.
Построим на этих векторах как на сторонах
параллелограммОАСВ.
Вектор ![]() –
диагональ параллелограмма – является
суммой векторов
–
диагональ параллелограмма – является
суммой векторов![]() и
и![]() (рис.
2).
(рис.
2).
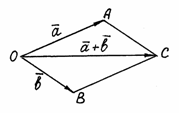
Рис. 2
Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).

Рис. 3
Вычитание
векторов. Разностью ![]() векторов
векторов![]() и
и![]() называется
такой вектор
называется
такой вектор![]() ,
который в сумме с вектором
,
который в сумме с вектором![]() дает
вектор
дает
вектор![]() :
:![]()
![]() .
.
Если
векторы ![]() и
и![]() привести
к общему началу, то разность представляет
собой отрезок, соединяющий их концы и
направленный от «вычитаемого» к
«уменьшаемому» (рис. 4).
привести
к общему началу, то разность представляет
собой отрезок, соединяющий их концы и
направленный от «вычитаемого» к
«уменьшаемому» (рис. 4).

Рис. 4
Таким
образом, если на векторах ![]() и
и![]() ,
отложенных из общей точкиО,
построить параллелограмм ОАСВ,
то вектор
,
отложенных из общей точкиО,
построить параллелограмм ОАСВ,
то вектор ![]() ,
совпадающий с одной диагональю, равен
сумме
,
совпадающий с одной диагональю, равен
сумме![]() ,
а вектор
,
а вектор![]() ,
совпадающий с другой диагональю, –
разности
,
совпадающий с другой диагональю, –
разности![]() (рис.
5).
(рис.
5).
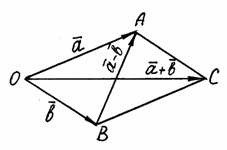
Рис. 5
Умножение
вектора на число. Произведением вектора ![]() на
действительное число
на
действительное число![]() называется
вектор
называется
вектор![]() (обозначают
(обозначают![]() ),
определяемый следующими условиями:
),
определяемый следующими условиями:
1) ![]() ,
,
2) ![]() при
при![]() и
и![]() при
при![]() .
.
Очевидно,
что при ![]()
![]() .
.
Построим,
например, векторы ![]() и
и![]() для
заданного вектора
для
заданного вектора![]() (рис.
6).
(рис.
6).
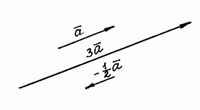
Рис. 6
Из
определения следует: два
вектора ![]() и
и![]() коллинеарны
тогда и только тогда, когда имеет место
равенство
коллинеарны
тогда и только тогда, когда имеет место
равенство![]() :
:
![]() (2.1)
(2.1)
Свойства линейных операций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;![]() ;
;
Пусть
дан вектор ![]() .Ортом вектора
.Ортом вектора ![]() (обозначается
(обозначается![]() )
называется вектор единичной длины,
сонаправленный с вектором
)
называется вектор единичной длины,
сонаправленный с вектором![]() .
.
Очевидно, ![]() для
любого вектора
для
любого вектора![]() .
.
|
|
|
|
|
|
Билет 4
1) Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
![]() (*)
(*)
(разложение по элементам i-й строки);
![]() (**)
(**)
(разложение по элементам j-го столбца).
Убедимся в справедливости теоремы Лапласа на примере определителя матрицы третьего порядка. Разложим его вначале по элементам первой строки
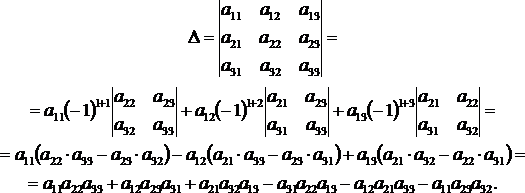
2)Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»). Для того чтобы вектор а был коллинеарен ненулевому вектору b, необходимо и достаточно, чтобы существовало число k, удовлетворяющее условию a = kb.
Билет 5
1) Метод Крамера является методом решения квадратной системы линейных алгебраических уравнений.
Рассмотрим стандартную линейную систему трех уравнений.
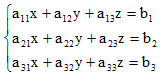 (2)
(2)
Под решением системы понимается всякая тройка чисел (х,у,z), удовлетворяющая этой системе, т.е. при подстановке которых в систему линейных уравнений получаются верные равенства.
Введем
определитель системы
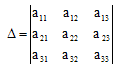 ,
и дополнительные определители
,
и дополнительные определители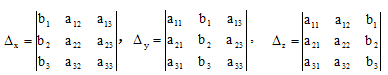
Если
определитель ![]() системы
(2) отличен от нуля, то существует, и
притом единственное, решение этой
системы, и оно выражается формулами
системы
(2) отличен от нуля, то существует, и
притом единственное, решение этой
системы, и оно выражается формулами![]() (3)
(3)
Формулы (3) называются формулами Крамера.
Неизвестные стандартной линейной системы с ненулевым определителем представляют собой дроби, знаменатели которых есть определитель системы, а числители равны соответствующим дополнительным определителям.
Замечание: Если определитель системы равен 0, то система (2) или несовместна или имеет бесконечно много решений.
2) Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны.Три вектора, среди которых имеются два коллинеарных, также компланарны.Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными (не лежать в одной плоскости).
Признак компланарности трех векторов
|
Если
вектор
где хиу—
некоторые числа, то векторы
|
|
Билет 6
1)Матрицей m × n называется прямоугольный массив чисел, состоящий из m строк и n столбцов. Количество строк и столбцов определяет размер матрицы. Отдельный элемент матрицы идентифицируется путем указания его строки и столбца в состоящем из двух элементов спсике индексов; первый индекс определяет строку, а второй — столбец. Ниже в качестве примера приведены матрицы M размером 3 × 3, В размером 2 × 4 и С размером 3 × 2:
Две матрицы считаются равными, если они имеют одинаковую размерность и их соответствующие элементы равны. Например, A = C, поскольку матрицы A и C имеют одинаковую размерность и их соответствующие элементы равны. Мы говорим, что A ≠ B и A ≠ D поскольку у этих матриц либо разная размерность, либо не равны соответствующие элементы.
Сложение и вычитание матриц - одно из простейших действий над ними, т.к. необходимо сложить или отнять соответствующие элементы двух матриц. Главное помнить, что складывать и вычитать можно только матрицы одинаковых размеров, т.е. тех, у которых одинаковое количество строк и одинаковое количество столбцов.
Например, пусть даны две матрицы равного размера 2х3, т.е. с двумя строками и тремя столбцами:

Сумма двух матриц:
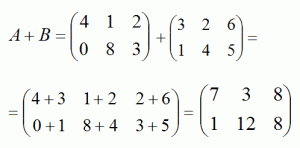
Разность двух матриц:
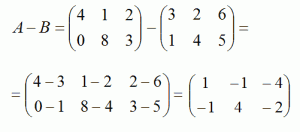
2. Умножение матрицы на число:
Умножение матрицы на число - процесс, заключающийся в умножении числа на каждый элемент матрицы.
Например, пусть дана матрица А:
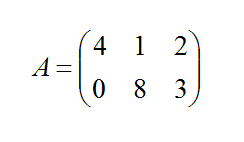
Умножим число 3 на матрицу А:
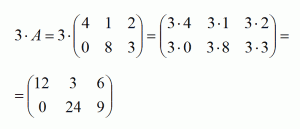
2)
Мы рассмотрели умножение вектора на
число. Однако во многих задачах механики
и физики встречается операция умножения
вектора на вектор. Но при этом результат
может быть как числом, так и вектором.
Поэтому рассматривают два вида умножения
векторов: скалярное и векторное.

Пусть
даны два вектора ![]() и
и![]() ,
угол между, которыми равен
,
угол между, которыми равен![]() .
.
Скалярным произведением
векторов ![]() и
и![]() называется
число, равное произведению длин этих
векторов на косинус угла между ними.
Скалярное произведение обозначается
называется
число, равное произведению длин этих
векторов на косинус угла между ними.
Скалярное произведение обозначается![]() .
Итак,
.
Итак,![]() .
.
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов
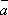 и
и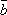
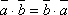 .
.
Очевидно, из определения скалярного произведения:
![]() .
.
Для любого числа λ и любых векторов
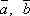 имеем:
имеем:
![]() .
.
Доказательство.
Ограничимся случаем, когда λ > 0. В этом
случае угол между векторами ![]() и
и![]() совпадает
с углом между векторами
совпадает
с углом между векторами![]() и
и![]() ,
,![]() .
.
Поэтому ![]() .
Откуда
.
Откуда![]()
Аналогично
доказывается и равенство ![]() .
.
Случай λ <0 рассмотреть самостоятельно.
Для любых векторов
 выполняется
равенство
выполняется
равенство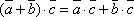 .
.
Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь
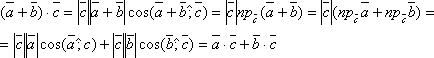
Для любого вектора
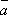 выполняется
соотношение
выполняется
соотношение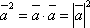 .
.
Действительно,
так как ![]() ,
то
,
то![]() .
.
Из
этого свойства в частности следует ![]() .
.
Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это свойство очевидно из определения скалярного произведения.
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Пример. Дан
вектор ![]() .
Известно, что
.
Известно, что![]()
Найти ![]() .
.
Имеем![]() ,
т.е.
,
т.е.![]() .
.
Найдем: ![]()
Следовательно, ![]() .
.
Билет 7
1) Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя.
Пример. ![]()
Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата
![]()
Элемент ci,j матрицы – ответа принадлежащий i-ой строке и j-му столбцу, вычисляется как произведение i-ой строки первого сомножителя An,m на j-ый столбец второго сомножителяBm,k. Так, например, при вычислении элемента умножается первая строка на третий столбец, а при вычислении элемента умножается третья строка на первый столбец.
Можно перемножать только те строки и столбцы, у которых одинаковое число элементов (смотри условие возможности умножения матриц). В результате получается число, равное сумме произведений соответствующих элементов (первый элемент строки на первый элемент столбца плюс второй элемент строки на второй элемент столбца и т. д. и, наконец, плюс произведение последних элементов).
Рассмотрим умножение матриц на примере :
![]()
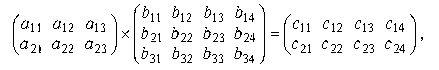
где

. 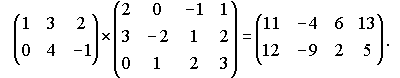
2) Введем сначала понятие ориентации тройки векторов.
Пусть
даны три некомпланарных вектора ![]() с
общим началом, перечисленных в определенном
порядке: первый –
с
общим началом, перечисленных в определенном
порядке: первый –![]() ,
второй –
,
второй –![]() ,
третий –
,
третий –![]() .
.
Тройка
некомпланарных
векторов ![]() называетсяправоориентированной или
простоправой,
если из конца третьего вектора кратчайший
поворот от первого ко второму виден
против часовой стрелки. В противном
случае тройку векторов называют левой,
в этом случае если мы будем смотреть с
конца вектора
называетсяправоориентированной или
простоправой,
если из конца третьего вектора кратчайший
поворот от первого ко второму виден
против часовой стрелки. В противном
случае тройку векторов называют левой,
в этом случае если мы будем смотреть с
конца вектора ![]() ,
то кратчайший поворот от
,
то кратчайший поворот от![]() к
к![]() осуществляется
по часовой стрелке.
осуществляется
по часовой стрелке.
Векторным
произведением векторов ![]() и
и![]() называется
новый вектор
называется
новый вектор![]() ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
Длина вектора
 равна
площади параллелограмма, построенного
на векторах
равна
площади параллелограмма, построенного
на векторах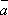 и
и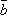 .
.
Вектор
 перпендикулярен
плоскости этого параллелограмма.
перпендикулярен
плоскости этого параллелограмма.Он направлен так, что векторы
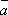 и
и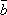 образуют
правую тройку векторов.
образуют
правую тройку векторов.
Векторное
произведение векторов ![]() и
и![]() обозначается
символом
обозначается
символом![]() .
Если хотя бы один из сомножителей равен
нулю, то векторное произведение по
определению считают равным нулю
.
Если хотя бы один из сомножителей равен
нулю, то векторное произведение по
определению считают равным нулю
Векторное произведение обладает следующими свойствами:
Из определения следует, что длина векторного произведения численно равна площади параллелограмма, построенного на векторах, и, следовательно, находится по формуле:
![]() .
.
Таким
образом, ![]() и
и![]() .
.
При перестановке сомножителей векторное произведение меняет свой знак
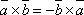 .
.
Действительно
из определения векторного произведения
следует, что векторы ![]() и
и![]() имеют
одинаковые модули, расположены на одной
прямой, но направлены в противоположные
стороны. Поэтому, векторы
имеют
одинаковые модули, расположены на одной
прямой, но направлены в противоположные
стороны. Поэтому, векторы![]() и
и![]() являются
противоположными векторами и поэтому
являются
противоположными векторами и поэтому![]() .
.
Скалярный множитель можно выносить за знак векторного произведения, т.е. для любого числа λ и любых векторов
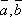
![]() .
.
Доказательство
этого свойства непосредственно следует
из определения векторного произведения.
Докажем для λ > 0. В этом случае ![]() .
Тогда по определению векторного
произведения
.
Тогда по определению векторного
произведения
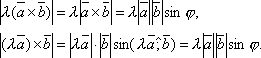
Вектор ![]() перпендикулярен
векторам
перпендикулярен
векторам![]() и
и![]() .
Вектор
.
Вектор![]() также
также![]() векторам
векторам![]() и
и![]() ,
т.к. векторы
,
т.к. векторы![]() и
и![]() ,
,![]() и
и![]() лежат
в одной плоскости. Следовательно,
векторы
лежат
в одной плоскости. Следовательно,
векторы![]() и
и![]() коллинеарны.
Очевидно, что направления их также
совпадают. Т. к.
коллинеарны.
Очевидно, что направления их также
совпадают. Т. к.![]() ,
и следовательно,
,
и следовательно,![]() ,
то
,
то![]() .
.
Поэтому ![]() .
.
Аналогично проводится доказательство для случая λ < 0.
Для любых векторов
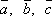 имеет
место равенство
имеет
место равенство
![]() .
.
Примем без доказательства.
Векторное произведение двух векторов равно нулевому вектору тогда и только тогда, когда один из сомножителей равен нулю или векторы коллинеарны.
Действительно,
если векторы коллинеарны, то ![]() ,
т.е. площадь параллелограмма, построенного
на данных векторах,равна нулю.
,
т.е. площадь параллелограмма, построенного
на данных векторах,равна нулю.
Таким образом, для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулевому вектору.
В
частности ![]() .
.
Билет 8
1) Матрица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Иногда рассматривают многомерные матрицы или матрицы непрямоугольной формы. Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица. Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.
Элементарными преобразованиями матрицы называются следующие преобразования: 1) умножение строки матрицы на число, отличное от нуля; 2) прибавление к одной строке матрицы другой строки; 3) перестановка строк; 4) вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) транспонирование матрицы;
2)
Смешанным произведением векторов ![]() называется
число
называется
число![]() ,
равное скалярному произведению
вектора
,
равное скалярному произведению
вектора![]() на
векторное произведение векторов
на
векторное произведение векторов![]() и
и![]() .
Смешанное произведение обозначается
.
Смешанное произведение обозначается![]() .
.
Геометрические свойства смешанного произведения
1.
Модуль смешанного произведения
некомпланарных векторов ![]() равен
объему
равен
объему![]() параллелепипеда,
построенного на этих векторах.
Произведение
параллелепипеда,
построенного на этих векторах.
Произведение![]() положительно,
если тройка векторов
положительно,
если тройка векторов![]() —
правая, и отрицательно, если тройка
—
правая, и отрицательно, если тройка![]() —
левая, и наоборот.
—
левая, и наоборот.
2.
Смешанное произведение ![]() равно
нулю тогда и только тогда, когда
векторы
равно
нулю тогда и только тогда, когда
векторы![]() компланарны:
компланарны:
![]() векторы
векторы ![]() компланарны.
компланарны.
Докажем
первое свойство. Найдем по определению
смешанное произведение: ![]() ,
где
,
где![]() —
угол между векторами
—
угол между векторами![]() и
и![]() .
Модуль векторного произведения (по
геометрическому свойству 1) равен
площади
.
Модуль векторного произведения (по
геометрическому свойству 1) равен
площади![]() параллелограмма,
построенного на векторах
параллелограмма,
построенного на векторах![]() и
и![]() : .
Поэтому
: .
Поэтому![]() .
Алгебраическое значение
.
Алгебраическое значение![]() длины
проекции вектора
длины
проекции вектора![]() на
ось, задаваемую вектором
на
ось, задаваемую вектором![]() ,
равно по модулю высоте
,
равно по модулю высоте![]() параллелепипеда,
построенного на векторах
параллелепипеда,
построенного на векторах![]() (рис.
1.47). Поэтому модуль смешанного произведения
равен объему
(рис.
1.47). Поэтому модуль смешанного произведения
равен объему![]() этого
параллелепипеда:
этого
параллелепипеда:
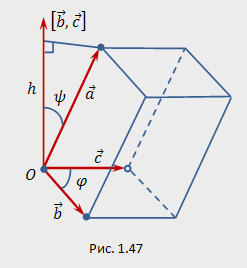
Знак
смешанного произведения определяется
знаком косинуса угла ![]() .
Если тройка
.
Если тройка![]() правая,
то
правая,
то![]() и
смешанное произведение
и
смешанное произведение![]() положительно.
Если же тройка
положительно.
Если же тройка![]() левая,
то
левая,
то![]() и
смешанное произведение
и
смешанное произведение![]() отрицательно.
отрицательно.
Докажем
второе свойство. Равенство ![]() возможно
в трех случаях:
возможно
в трех случаях:![]() или
или![]() (т.е.
(т.е.![]() ),или
),или![]() (т.е.
вектор
(т.е.
вектор![]() принадлежит
плоскости векторов
принадлежит
плоскости векторов![]() и
и![]() ).
В каждом случае векторы
).
В каждом случае векторы![]() компланарны
(см.
разд. 1.1).
компланарны
(см.
разд. 1.1).
Алгебраические свойства смешанного произведения
1. При перестановке двух множителей смешанное произведение изменяет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение не изменяется:
![]()
2. Смешанное произведение линейно по любому множителю.
Первое свойство следует из геометрического свойства 1 и свойств ориентации троек векторов (см. разд. 1.9), поскольку от перестановки двух множителей модуль смешанного произведения не изменяется, а меняется только ориентация тройки. При циклической перестановке векторов ориентация тройки не изменяется.
Билет 9
1) Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1.Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Пусть
дана квадратная матрица ![]() .
Требуется найти обратную матрицу
.
Требуется найти обратную матрицу![]() .
.
Первый способ.
1. Вычислить
определитель ![]() данной
матрицы. Если
данной
матрицы. Если![]() ,
то обратной матрицы не существует
(матрица
,
то обратной матрицы не существует
(матрица![]() вырожденная).
вырожденная).
2. Составить
матрицу ![]() из
алгебраических дополнений
из
алгебраических дополнений![]() элементов
матрицы
элементов
матрицы![]() .
.
3. Транспонируя
матрицу ![]() ,
получить присоединенную матрицу
,
получить присоединенную матрицу![]() .
.
4. Найти
обратную матрицу (4.1), разделив все
элементы присоединенной матрицы на
определитель ![]()
![]()
Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.
1. Составить
блочную матрицу ![]() ,
приписав к данной матрице
,
приписав к данной матрице![]() единичную
матрицу того же порядка.
единичную
матрицу того же порядка.
2. При
помощи элементарных преобразований,
выполняемых над строками матрицы ![]() ,
привести ее левый блок
,
привести ее левый блок![]() к
простейшему виду
к
простейшему виду![]() .
При этом блочная матрица приводится к
виду
.
При этом блочная матрица приводится к
виду![]() ,
где
,
где![]() —
квадратная матрица, полученная в
результате преобразований из единичной
матрицы
—
квадратная матрица, полученная в
результате преобразований из единичной
матрицы![]() .
.
3. Если ![]() ,
то блок
,
то блок![]() равен
обратной матрице, т.е.
равен
обратной матрице, т.е.![]() .
Если
.
Если![]() ,
то матрица
,
то матрица![]() не
имеет обратной.
не
имеет обратной.
В
самом деле, при помощи элементарных
преобразований строк матрицы ![]() можно
привести ее левый блок
можно
привести ее левый блок![]() к
упрощенному виду
к
упрощенному виду![]() (см.
рис. 1.5). При этом блочная матрица
(см.
рис. 1.5). При этом блочная матрица![]() преобразуется
к виду
преобразуется
к виду![]() ,
где
,
где![]() —
элементарная матрица, удовлетворяющая
равенству
—
элементарная матрица, удовлетворяющая
равенству![]() .
Если матрица
.
Если матрица![]() невырожденная,
то согласно п.2 замечаний 3.3 ее упрощенный
вид совпадает с единичной матрицей
невырожденная,
то согласно п.2 замечаний 3.3 ее упрощенный
вид совпадает с единичной матрицей![]() .
Тогда из равенства
.
Тогда из равенства![]() следует,
что
следует,
что![]() .
Если же матрица
.
Если же матрица![]() вырожденная,
то ее упрощенный вид
вырожденная,
то ее упрощенный вид![]() отличается
от единичной матрицы, а матрица
отличается
от единичной матрицы, а матрица![]() не
имеет обратной.
не
имеет обратной.
2) Различные виды уравнения прямой на плоскости
Уравнение прямой с угловым коэффициентом
у = kx + b
b

(!) Не существует для прямых,
параллельных оси Оу
Общее уравнение прямой
р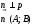
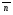

Уравнение прямой с данным вектором нормали
и проходящей через данную точку
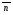
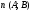
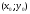
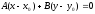
Уравнение прямой в отрезках
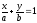
(!) Не существует для прямых,
параллельных осям координат
Уравнение с данным направляющим вектором и проходящей через данную точку
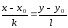
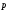
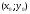
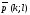
Уравнение прямой, проходящей через две данные точки




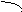


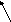

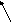










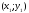
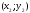
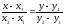
Билет 10
1)


2) Если две прямые l1 и l2 лежат на плоскости, то возможны три различных случая их взаимного расположения: 1)пересекаются (т.е. имеют одну общую точку); 2) параллельны и не совпадают; 3) совпадают.
Выясним, как узнать, какой из этих случаев имеет место, если эти прямые заданы своими уравнениями в общем виде:
![]() (12)
(12)
Если прямые l1 и l2 пересекаются в некоторой точке М(х,у), то координаты этой точки должны удовлетворять обоим уравнениям системы (12).
Следовательно, чтобы найти координаты точки пересечения прямых l1 и l2, надо решить систему уравнений (12): 1) если система (12) имеет единственное решение, то прямые l1 и l2 пересекаются; 2) если система (12) не имеет решения, то прямые l1 и l2 параллельны; 3) если система (12) имеет множество решений, то прямые l1 и l2 совпадают
Билет 11
1)
Линейное,
или векторное
пространство ![]() над полем P —
это непустое
множество L,
на котором введены операции
над полем P —
это непустое
множество L,
на котором введены операции
сложения, то есть каждой паре элементов множества
 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый 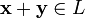 и
иумножения на скаляр (то есть элемент поля P), то есть любому элементу
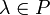 и
любому элементу
и
любому элементу 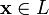 ставится
в соответствие единственный элемент
из
ставится
в соответствие единственный элемент
из 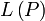 ,
обозначаемый
,
обозначаемый 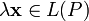 .
.
При этом на операции накладываются следующие условия:
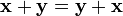 ,
для любых
,
для любых 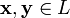 (коммутативность
сложения);
(коммутативность
сложения);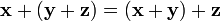 ,
для любых
,
для любых 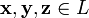 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
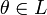 ,
что
,
что 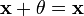 для
любого
для
любого 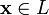 (существование
нейтрального элемента относительно
сложения),
в частности L не
пусто;
(существование
нейтрального элемента относительно
сложения),
в частности L не
пусто;для любого
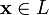 существует
такой элемент
существует
такой элемент 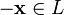 ,
что
,
что  (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).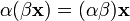 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр);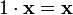 (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).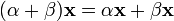 (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров);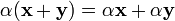 (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Следствия: 1. В любом линейном пространстве нулевой вектор единственен. 2. Для любого вектора a существует единственный противоположный элемент. 3. Для любого a,b из V уравнение a+x=b имеет единственное решение. 4. Для любого а из V верно: 0*a=o. Док-во: a+0a=1a+0a=(1+0)a=1a=a. 7. Для любого a из V верно: (-1)а=а.
2)
Окружность –
множество всех точек плоскости,
равноудаленных от данной точки на
плоскости.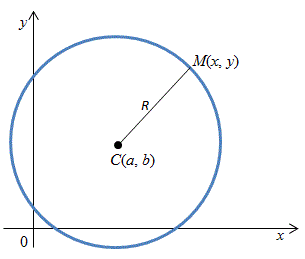
Выведем уравнение окружности.
Пусть C(a, b) – центр окружности, а R – ее радиус. Возьмем произвольную точку M(x, y) ∈ окр.
Расстояние
от центра окружности до точки M находится
по известной формуле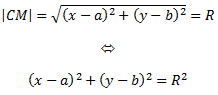
Каноническое уравнение окружности. В центре с координатами a и b и радиусом R
Если
в этом уравнении раскрыть скобки и
выполнить некоторые преобразования,
то получим: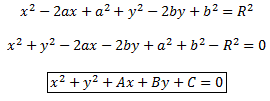
Приведение
уравнения окружности к каноническому
виду: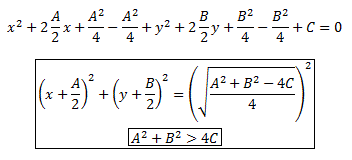
Билет 12
1)
Набор векторов ![]() называетсясистемой
векторов.
называетсясистемой
векторов.
Система
из ![]() векторов
векторов![]() называетсялинейно
зависимой,
если существуют такие числа
называетсялинейно
зависимой,
если существуют такие числа ![]() ,
не все равные нулю одновременно, что
,
не все равные нулю одновременно, что
![]()
Система
из ![]() векторов
векторов![]() называетсялинейно
независимой, если
равенство (1.1) возможно только при
называетсялинейно
независимой, если
равенство (1.1) возможно только при ![]() ,
т.е. когда линейная комбинация в левой
части (1.1) тривиальная.
,
т.е. когда линейная комбинация в левой
части (1.1) тривиальная.
Замечания 1.2.
1.
Один вектор ![]() тоже
образует систему: при
тоже
образует систему: при![]() -
линейно зависимую, а при
-
линейно зависимую, а при![]() -
линейно независимую.
-
линейно независимую.
Любая часть системы векторов называется подсистемой.
Свойства
Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
2)
Эллипсом называется
геометрическое место точек плоскости,
сумма расстояний от каждой из которых
до двух заданных точек ![]() ,
и
,
и ![]() есть
величина постоянная
есть
величина постоянная ![]() ,
бо́льшая расстояния
,
бо́льшая расстояния ![]() между
этими заданными точками (рис.3.36,а). Это
геометрическое определение выражаетфокальное
свойство эллипса.
между
этими заданными точками (рис.3.36,а). Это
геометрическое определение выражаетфокальное
свойство эллипса.