
2 Кинематика
.pdf
РАЗДЕЛ ВТОРОЙ КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА
ГЛАВА 5. КИНЕМАТИКА ТОЧКИ
5.1. Введение в кинематику
Кинематика – раздел теоретической механики, в котором изучается движение тел без учета действия сил, вызывающих или поддерживающих это движение.
Движением тела называется изменение его положения в пространстве по отношению к заданной системе отсчета.
Системой отсчета называют любое тело, по отношению к которому изучается движение.
Время в механике считается независимым переменным, одинаковым для всех наблюдателей.
В отдельных случаях при движении некоторых тел можно пренебречь их размерами и принимать их за геометрические точки. Это позволяет значительно упростить изучение характеристик движения тел.
Для изучения движения тела оно должно быть каким-то образом задано.
5.2. Способы задания движения точки
5.2.1. Координатный способ задания движения точки
В этом случае должны быть заданы координаты точки в виде некоторых функций времени (рис. 2.1):
Уравнения (2.1) являются уравнениями движения точки в декартовых координатах.
43

z |
- траектория |
|
|
|
|
|
|
||
|
|
точки |
X f1(t), |
|
|
|
M |
|
|
0 |
Z |
y |
Y f2 (t), |
(2.1) |
x |
|
X |
Z f3(t). |
|
Y |
|
|
|
|
Рис. 2.1.
Траекторию точки можно получить в явном виде, для чего надо исключить из уравнений (2.1) время.
Пример 2.1. Найти уравнение траектории точки, если ее
движение задано уравнениями:
X 3 cos(2 t), м, Y 3 sin(2 t), м.
Перепишем уравнения в виде
X |
cos(2 t), |
Y |
sin(2 t), |
|
3 |
3 |
|||
|
|
возведем |
в |
квадрат |
и |
y |
|
|
сложим. Получим: |
|
|
|
|||
|
|
|
|
|||
X2 Y2 |
32. |
|
|
|
||
Таким образом, в данном |
|
|
||||
случае |
точка |
движется |
по |
|
M0 |
|
окружности (рис. 2.2). Началь- |
|
|||||
|
|
|||||
ное положение |
точки опреде- |
0 |
x |
|||
ляется |
|
координатами |
|
|
||
X0 3м , Y0 0 . |
|
|
|
|
||
5.2.2. Векторный способ |
|
|
|
|||
задания движения |
|
Рис. 2.2. |
|
|||
В |
этом случае |
должна |
быть задана векторная функция времени |
||
|
|
(2.2) |
r |
f(t), |
|
44
которая и является уравнением движения точки в векторной форме (рис. 2.3).
Для перехода от векторного к координатному способу можно воспользоваться уравнением
|
|
|
|
|
r |
x i |
y j z k. |
(2.3) |
|
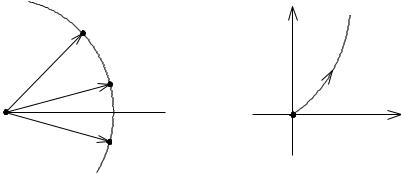
Пример 2.2. Определить траекторию точки, если уравнение ее движения имеет вид:
|
(2 t) |
|
|
|
|
|
|
r |
i |
(3 t 2 ) k. |
|
|
|
||
Очевидно, |
X 2 t; |
Y 0; |
Z 3 t 2 , |
то есть точка дви- |
|||
жется в плоскости 0XZ. |
|
|
|
|
|||
|
|
|
|
|
x |
|
|
|
M0 |
|
|
|
|
|
|
|
– траектория точки |
|
|
||||
r0 |
|
|
|
|
|
|
|
|
r1 |
|
M |
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
0 |
M0 |
y |
|
M2 |
|
|
||||
|
r |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Рис. 2.3. |
|
|
|
Рис. 2.4. |
|
|
Исключая |
|
из уравнений |
движения |
время получим |
|||
z 0.75 x 2 , следовательно в данном случае точка движется по параболе (рис. 2.4).
5.2.3. Естественный способ задания движения
При этом способе должны быть заданы (рис. 2.5):
1)траектория точки;
2)закон движения в виде зависимости криволинейной координаты S от времени, то есть
S f(t); |
(2.4) |
3)начало отсчета;
4)направление отсчета.
45

- 0
A
S
Рис. 2.5.
|
Если начало и направле- |
|
ние отсчета не заданы, они мо- |
|
гут быть выбраны произвольно. |
M |
Можно установить связь |
B |
между естественным и коорди- |
|
натным способами задания |
|
движения. Известно, что дугу |
|
можно выразить через коорди- |
|
наты: |
ds |
dx 2 dy2 |
dz2 . |
(2.5) |
||||
Найдем закон движения в примере 2.1: |
|||||||
|
dx |
6 sin(2t), |
|
dy |
6 cos(2t), |
dx 6 sin(2t)dt, |
|
|
dt |
|
|
dt |
|
||
dy 6 cos(2t)dt,
ds 
 62 (sin 2 (2t) cos2 (2t)(dt)2 6dt,
62 (sin 2 (2t) cos2 (2t)(dt)2 6dt,
ds 6 dt, S 6 t S0.
5.3.Определение скорости точки
Скоростью |
точки называется характеристика |
|||
положения точки с течением |
|
|||
времени по отношению к за- |
M1 |
|||
данной системе отсчета. |
|
|||
5.3.1. Векторный способ за- |
M0 |
|||
дания движения точки |
|
|||
r |
||||
В соответствии с приве- |
|
|||
денным |
выше |
определением |
r1 |
|
скорости |
найдем |
соответству- |
||
ющие приращения времени и |
|
|||
радиуса вектора (рис. 2.6): |
r0 |
|||
|
||||
Δt t1 t 0 , |
0 |
|||
|
|
|
|
|
r |
r1 |
r0 , |
Рис. 2.6. |
|
|
|
|
|
|
изменения
Vср
46

r
Тогда Δt Vср .
Таким образом, средняя скорость точки равна отношению приращения радиуса вектора к соответствующему промежутку времени. Истинное значение скорости найдется как предел:
lim |
|
|
|
(2.6) |
|
r |
dr |
V . |
|||
|
|
|
|
|
|
Δt 0 Δt |
|
dt |
|
|
|
Истинное значение скорости определяется векторной производной от радиуса-вектора по времени. Скорость определяется не только величиной, но и направлением. Вектор скорости всегда направлен по касательной к траектории точки в заданный момент времени.
5.3.2. Координатный способ задания движения
Перейдем от координатного способа задания движения к векторному на основе (2.3). Тогда с учетом (2.6) имеем
|
dx |
|
|
|
dy |
|
dz |
|
|
|
|||
V |
|
|
i |
|
|
j |
|
|
k. |
|
(2.7) |
||
dt |
dt |
dt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
||
V |
dx |
x, V |
dy |
|
y, V |
dz |
z. |
||||||
x |
|
dt |
|
|
|
y |
dt |
z |
dt |
|
|||
|
|
|
|
|
|
|
|
|
|||||
Следовательно проекции скорости на координатные оси определяются первыми производными по времени от соответствующих координат. Модуль скорости
V Vx2 Vy2 Vz2 . |
(2.8) |
Направляющие косинусы вектора скорости относительно координатных осей определяются выражениями (рис. 2.7):
cos( ) VVx , cos( ) VVy , cos( ) VVz .
47

|
|
|
|
|
5.3.3. Естественный способ |
|||||
y |
|
|
|
задания движения |
||||||
|
vy |
|
|
|
Дана траектория точ- |
|||||
|
|
|
v |
|
|
|||||
|
|
|
|
|
ки и закон изменения коор- |
|||||
|
|
|
|
динаты по этой траектории |
||||||
|
|
|
S S(t). |
|
|
|
||||
|
|
|
|
|
|
|
||||
|
M |
vx |
|
|
Пусть в момент вре- |
|||||
|
|
|
|
|||||||
0 |
|
|
|
x |
мени t |
точка занимала по- |
||||
|
|
|
ложение М, а в момент вре- |
|||||||
|
Рис. 2.7. |
|
|
|||||||
|
|
|
мени |
|
t1 |
положение |
М1 |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
(рис. 2.8). |
|
|
|
||
- 0 |
|
M |
|
|
За |
время |
Δt t1 t |
|||
|
|
|
|
|
||||||
|
|
|
M1 |
координата получила |
при- |
|||||
A |
S |
|
S |
|||||||
|
|
B |
ращение |
Δs s1 s , |
тогда |
|||||
|
|
|
||||||||
|
|
S1 |
|
|
Vср |
Δs |
, то есть средняя |
|||
|
|
|
|
|
Δt |
|||||
|
|
|
|
|
|
|
|
|
||
|
Рис. 2.8. |
|
|
скорость равна отношению |
||||||
|
|
|
приращения криволинейной |
|||||||
|
|
|
|
|
||||||
координаты к соответствующему промежутку времени. |
|
|||||||||
Для нахождения истинной скорости перейдем к пределу |
||||||||||
V |
lim |
Δs ds , |
то есть V ds . |
|
|
|
|
(2.9) |
||
|
Δt 0 |
Δt |
dt |
|
dt |
|
|
|
|
|
Численное значение скорости точки при естественном спо- |
||||||||||
собе задания движения определяется первой производной по |
||||||||||
времени от криволинейной координаты. Скорость всегда направ- |
||||||||||
лена по касательной к траектории точки. |
|
|
|
|
|
|||||
Пример 2.3. Определить скорость точки при t = 1 c, для ее |
||||||||||
движения по закону |
S t 2 3 t 2 , м. На основе (2.9) находим |
|||||||||
V |
dS |
|
2t 9t 2 . Для заданного момента времени |
|
dt |
||||
|
|
|||
Vt 2 - 9 7 м/с, то есть скорость направлена влево (рис. 2.8).
Пример 2.4. Точка M движется в соответствии с уравнени-
ями
48
x 2sin(4t) , м; |
y 3cos(4t), м. |
|
|
|
|
|
(а) |
||||||
Определить величину и направление вектора скорости точ- |
|||||||||||||
ки и указать ее положение |
на траектории в |
момент |
времени |
||||||||||
t 24 c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Исключая время из уравнений движения, по ана- |
|||||||||||||
логии с примером 2.1, найдем уравнение траектории |
|
|
|
||||||||||
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
|
(б) |
4 9 |
1. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
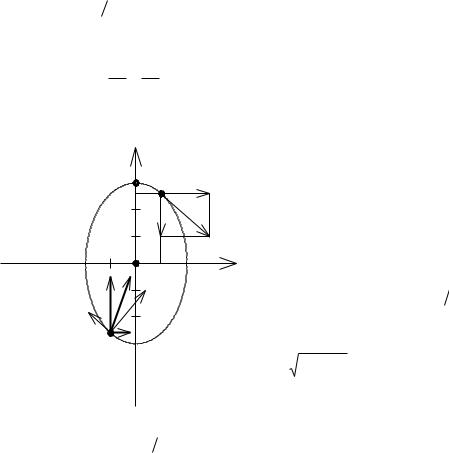
Следовательно, в данном случае точка движется по эллипсу |
|||||||||||||
(рис. 2.9). |
При |
t 0 |
точка |
M0 |
имела |
координаты |
|
x0 0 ; |
|||||
y |
|
|
|
|
|
y0 3 м. В заданный момент вре- |
|||||||
|
M0 M |
Vx |
|
мени |
t |
координаты |
|
точки |
|||||
|
|
|
|
|
|
x0 1,0 м, |
y0 2,6 м. |
Найдем |
|||||
|
|
|
|
|
|
проекции вектора скорости на оси |
|||||||
|
Vy |
|
|
|
координат: |
|
|
|
|
|
|
||
|
|
|
|
V |
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
Vx x 8cos(4t), |
|
м/с; |
|||||
|
|
|
|
|
|
|
|||||||
Wy |
|
|
|
|
Vy y 12sin(4t) , м/с. |
|
|
||||||
W |
|
|
|
x |
|
|
|||||||
|
|
|
|
|
|
При |
|
|
|
t 24 c ; |
|||
Wn |
|
|
|
Vx 6,9 м/c; |
Vy 6 м/c; |
тогда |
|||||||
W |
|
|
|
|
|
||||||||
Wx |
|
|
|
|
|
модуль |
|
|
|
|
скорости |
||
|
|
|
|
|
V |
x2 y2 |
9,14 |
|
|
|
|
||
|
|
|
|
|
|
м/с. |
Направ- |
||||||
Рис. 2.9. |
|
|
ление |
вектора |
скорости |
можно |
|||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
найти по его проекциям на оси ко- |
|||||||
ординат, |
или |
по |
направляющим |
косинусам. |
В |
частности, |
|||||||
|
|
V 0,756 ( 41o ). |
|
|
|
|
|
|
|
||||
cos(V,i) V |
Очевидно, |
при выполнении |
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рисунка в масштабе вектор скорости V , найденный по его про- |
|||||||||||||
екциям Vx |
и Vy , должен быть направлен по касательной к траек- |
||||||||||||
тории в точке M. |
|
|
|
|
|
|
|
|
|
|
|||
5.4. Определение ускорения точки
49

5.4.1. Векторный способ задания движения
Ускорением материальной точки называется векторная величина, характеризующая изменение во времени величины и направления вектора скорости.
Пусть точка движется по криволинейной траектории. В момент времени t она занимает положение М и имеет скорость V, а в момент времени t1 – положение М1 и скорость V1 (рис. 2.10).
|
За |
|
промежуток |
времени |
|
|
|
|
Δt t1 t вектор скорости из- |
M |
|
|
|||||
менится |
|
на |
величину |
|
V |
|
||
|
|
|
|
|
|
|
|
V |
V |
V1 |
V . Очевидно |
отно- |
Wср |
|
M1 |
||
шение |
|
|
|
|
|
V1 |
||
|
V |
|
|
|
|
|
||
|
Wср |
|
(2.10) |
|
|
|
||
|
t |
|
|
|
|
|
V1 |
|
|
есть среднее ускорение за |
|
|
|
||||
время Δt . Истинное значение |
|
|
|
|||||
ускорения |
найдется как |
предел |
|
Рис. 2.10. |
|
|||
отношения (2.10): |
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||
V |
|
dV |
|
|
||
W lim |
|
. |
(2.11) |
|||
|
|
|||||
Δt 0 |
Δt |
|
dt |
|
||
Ускорение точки определяется первой производной от вектора скорости по времени или второй производной от радиусвектора точки по времени
|
|
|
|
2 |
|
|
|
|
d |
|
|||
W |
dV |
|
r |
. |
(2.11’) |
|
|
|
|
||||
|
dt |
|
dt 2 |
|
||
Вектор ускорения всегда лежит в плоскости движения и направлен в сторону вогнутости траектории.
5.4.2. Координатный способ задания движения
Для определения ускорения в соответствии с (2.11) вычислим векторную производную от вектора скорости (2.7)
50

|
d2 x |
|
|
|
d2 y |
|
d2z |
|
|
|
|
|
|
(2.12) |
|||||
W |
dt 2 |
i |
dt 2 |
j |
dt 2 |
k. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из (2.12) вытекает: |
|
|
|
|
|
|
|
|
|
||||||||||
W |
d2 x |
|
dV |
x x, |
W |
d2 y |
|
dVy |
y, |
|
|||||||||
x |
|
dt 2 |
|
|
|
dt |
|
|
y |
|
dt 2 |
|
dt |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
(2.13) |
||||||||
|
|
d2z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
W |
|
|
dV |
|
z. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||
z |
|
dt 2 |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, проекции вектора ускорения на координат- |
|||||||||||||||||||
ные оси определяются вторыми производными от соответствую- |
|||||||||||||||||||
щих координат по времени. Модуль ускорения |
|
|
|
||||||||||||||||
W |
|
w 2y w 2y w z2 . |
|
|
|
|
|
|
|
(2.14) |
|||||||||
Направление вектора ускорения определяется через |
|||||||||||||||||||
направляющие косинусы: |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
W |
|
|
|
|
|
|
Wy |
|
|
|
W |
|
||||
|
|
|
|
x |
|
cos( ) W , |
|
|
|
|
z |
(2.15) |
|||||||
cos( ) W , |
cos( ) |
W . |
|||||||||||||||||
|
|||||||||||||||||||
5.4.3. Естественный способ задания движения |
|
||||||||||||||||||
Пусть точка движется по криволинейной траектории и в |
|||||||||||||||||||
момент времени t имеет скорость V, а в момент времени t1 – ско- |
|||||||||||||||||||
рость V1 (рис. 2.11). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Перенесем |
оси |
|
есте- |
|
|
|
|
|
|
|
|
||||||||
ственных координат из по- |
|
|
|
n1 |
|
|
|
||||||||||||
ложении М в положение М1. |
n |
|
|
|
|
|
V1 |
|
|||||||||||
В соответствии с (2.11) для |
|
|
V1n |
|
|
|
|||||||||||||
определения |
|
|
ускорения |
|
|
|
M1 |
|
|
||||||||||
необходимо вычислить пре- |
|
|
|
|
|
1 |
|||||||||||||
дел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.11. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51 |
|
W lim |
|
|
|
|
|
|
|
|||||
|
|
V |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Δt 0 Δt |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
V1 V |
. |
|
|
|||||||
|
Δt |
|
|
|||||||||
|
Δt 0 |
|
|
|
|
|
||||||
Спроектируем последнее уравнение на оси естественных |
||||||||||||
координат. |
|
|
|
|
|
|
|
|
|
|||
В проекции на ось Mτ получим |
|
|||||||||||
W |
lim |
V1 cos() V |
. |
|
||||||||
|
|
|
|
|
Δt |
|
||||||
|
Δt 0 |
|
|
|
|
|
|
|
||||
При t 0 , 0 , cos() 1, V1 V . |
|
|||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|||
W |
|
dV |
|
|
d2S |
. |
|
(2.16) |
||||
|
|
|
||||||||||
|
|
dt |
|
|
dt2 |
|
|
|
|
|||
Проекция ускорения на касательную, то есть касательное ускорение точки, определяется первой производной по времени от скорости или второй производной по времени от криволинейной координаты S.
Касательное ускорение характеризует изменение вектора скорости по величине. Если V const , то ускорение W 0 .
В проекции на ось Mn получим |
|
|
|||||||||||||
Wn lim |
V1 sin() 0 |
. |
|
|
|
|
|||||||||
|
|
Δt |
|
|
|
|
|
|
|
||||||
|
|
Δt 0 |
|
|
|
|
|
|
|
|
|
|
|||
Для вычисления предела умножим числитель и знамена- |
|||||||||||||||
|
ΔS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тель на |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
ΔS |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
sin( ) ΔS |
|
|
|
||||||
W |
lim |
V |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
n |
Δt 0 |
|
1 |
Δt ΔS |
|
|
|
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
sin( ) |
|
ΔS |
|
|
|
|
|
|||
lim V |
|
|
|
|
|
|
|
|
|
, |
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
|
|
|
Δt |
|
ΔS |
|
|
|
||||
|
Δt 0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
52
