
- •Кинематика
- •Основные определения
- •Способы задания движения
- •4. Взаимосвязь между некоторыми характеристиками различных способов задания движения.
- •Скорость точки
- •Определение скорости при векторном способе задания движения.
- •Определение скорости при координатном способе
- •Ускорение точки при координатном способе задания движения
- •Ускорение точки при естественном способе задания движения
- •Частные случаи движения точки
- •Кинематика твердого тела Поступательное движение твердого тела
- •Вращательное движение твердого тела
- •Определение линейных скоростей и ускорений точек вращающегося тела
- •Плоское движение твердого тела
- •Определение скоростей точек тела при плоском движении
- •Другие методы определения скоростей точек тела
- •Частные случаи определения положения мгновенного центра скоростей
- •Определение ускорения точек при плоском движении
- •Сложное движение
- •Определение абсолютной скорости точки
- •Определение абсолютного ускорения точки
Определение абсолютной скорости точки

Рассмотрим точку, совершающую сложное движение. Для нее будет справедливо выражение
![]() (48)
(48)
Разделим (48) на t и перейдем к пределу, в итоге получим
![]() .
(49)
.
(49)
Уравнение (49) выражает следующую теорему.
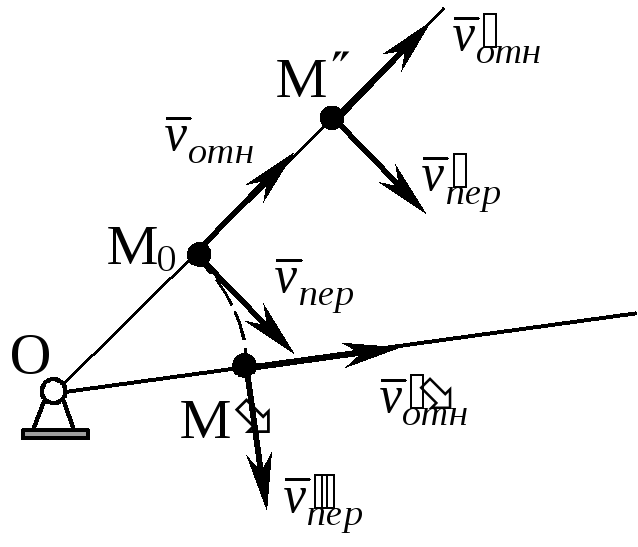
Теорема: Абсолютная скорость точки, совершающей сложное движение, равна геометрической сумме относительной и переносной скоростей.
Модуль абсолютной скорости можно найти по теореме косинусов
![]() ,
,
где
– угол между векторами
![]() и
и![]() .
.
Определение абсолютного ускорения точки
Возьмем векторную производную от (49)
![]() .
(50)
.
(50)
В уравнении (50):
![]()
 –относительное
ускорение;
–относительное
ускорение;
![]() –переносное
ускорение;
–переносное
ускорение;
![]() –поворотное
ускорение Кориолиса, характеризующее
изменение относительной скорости в
переносном движении и переносной
скорости в относительном движении.
–поворотное
ускорение Кориолиса, характеризующее
изменение относительной скорости в
переносном движении и переносной
скорости в относительном движении.
В итоге уравнение (50) принимает вид
![]() .
(51)
.
(51)
Уравнение (51) выражает следующую теорему Кориолиса.
Теорема: Абсолютное ускорение материальной точки по величине и направлению определяется геометрической суммой относительного ускорения, переносного ускорения и кориолисова ускорения.
Кориолисово ускорение точки равно удвоенному векторному произведению угловой скорости переносного движения на относительную линейную скорость
![]() .
(52)
.
(52)
Если
угол между векторами
![]() и
и![]() равен,
то
равен,
то
![]() .
(53)
.
(53)
Направлен
вектор кориолисова ускорения
перпендикулярно плоскости, проходящей
через векторы
![]() и
и
![]() ,
в ту сторону, откуда совмещение на
кратчайший угол
,
в ту сторону, откуда совмещение на
кратчайший угол
![]() с
с
![]() наблюдается происходящим против хода
часовой
стрелки.
наблюдается происходящим против хода
часовой
стрелки.
И з
уравнения (53)
следует, что кориолисово ускорение
обращается в ноль, когда:
з
уравнения (53)
следует, что кориолисово ускорение
обращается в ноль, когда:
1.
![]() =0,
переносное движение - поступательное,
=0,
переносное движение - поступательное,
2.
![]() =0,
=0,
3. .=0 или =, относительное движение происходит по направлению параллельному оси переносного вращения.
