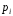- •Математика
- •Санкт-Петербург
- •Содержание
- •2. Методические указания к изучению дисциплины
- •3. Методические указания к выполнению контрольной работы
- •Контрольная работа №1
- •Тема 1. Решение матричных уравнений
- •Каждой квадратной матрице ставится в соответствие число
- •Пример1. Найти а-1 , если.
- •Пример2.
- •Тема 2. Решение систем линейных уравнений
- •Контрольные задания
- •Тема 3. Основы дифференциального исчисления
- •Контрольные задания
- •Тема 4. Функции двух переменных
- •Контрольные задания
- •Тема 5. Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования Непосредственное интегрирование
- •Замена переменой в неопределенном интеграле
- •Интегрирование по частям в неопределенном интеграле
- •Интегрирование рациональных дробей
- •Контрольные задания
- •Тема 6. Определенный интеграл
- •Контрольные задания
- •Тема 7. Дифференциальные уравнения
- •Уравнение с разделяющимися переменными
- •Однородное уравнение первого порядка
- •Линейное уравнение первого порядка
- •Контрольные задания
- •Тема 8. Ряды Рассмотрим выражение вида ,(1)
- •Контрольные задания
- •Контрольная работа №2
- •Тема 1. Случайные события
- •Контрольные задания
- •Тема 2. Случайные величины
- •Контрольные задания
- •Тема 3. Графический метод решения задачи линейного программирования
- •Контрольные задания
- •Тема 4. Симплекс-метод решения задачи линейного программирования
- •Контрольные задания
- •Тема 5. Транспортная задача
- •Контрольные задания
- •5. Требования к выполнению контрольной работы
- •6.1 Основная литература
- •6.1 Дополнительная литература
- •Содержание дисциплины
- •Тема 1.5. Дифференциальное исчисление функции нескольких переменных
- •Тема 3.2. Системы обыкновенных дифференциальных уравнений.
- •Образец оформления титульного листа
Контрольные задания
Дискретная случайная величина задана законом распределения. Найти:
1. Неизвестное
 ;
;
2.Математическое ожидание;
3.Дисперсию;
4.Вероятность попадания в интервал
 .
.
2.1.
|
|
0 |
4 |
5 |
10 |
11 |
15 |
|
|
0,3 |
0,1 |
0,1 |
0,1 |
|
0,1 |
 =5,
=5, =11
=11
2.2.
|
|
-4 |
-1 |
1 |
3 |
10 | |||||
|
|
0,4 |
0,2 |
0,3 |
|
0,1 | |||||
 =1,
=1, =3
=3
2.3.
|
|
-11 |
-2 |
-1 |
2 |
4 |
6 | ||||||
|
|
0,4 |
0,1 |
|
0,1 |
0,1 |
0,2 | ||||||
 =
-2,
=
-2, =4
=4
2.4.
|
|
-6 |
-2 |
-1 |
3 |
7 | |||||
|
|
0,4 |
0,1 |
|
0,2 |
0,1 | |||||
 =
-2,
=
-2, =7
=7
2.5.
|
|
-1 |
-0,5 |
2 |
3 |
4 |
5 | |||||
|
|
0,1 |
0,1 |
|
0,4 |
0,1 |
0,1 | |||||
 =
2,
=
2, =3
=3
2.6.
|
|
-3 |
-1 |
1 |
4 |
7 | |||||
|
|
0,2 |
0,1 |
|
0,2 |
0,2 | |||||
 =
1,
=
1, =7
=7
2.7.
|
|
4 |
5 |
7 |
9 |
12 | |||||
|
|
0,4 |
|
0,1 |
0,1 |
0,1 | |||||
 =
5,
=
5, =9
=9
2.8.
|
|
-1 |
3 |
5 |
6 |
9 | |||||
|
|
0,2 |
|
0,2 |
0,2 |
0,1 | |||||
 =
3,
=
3, =9
=9
2.9.
|
|
2 |
3 |
6 |
9 |
10 |
13 | ||||||
|
|
0,2 |
0,1 |
|
0,2 |
0,1 |
0,1 | ||||||
 =3,
=3, =10
=10
2.10.
|
|
-1 |
0 |
1 |
5 |
6 |
8 | ||||||
|
|
0,3 |
0,2 |
0,1 |
0,1 |
|
0,1 | ||||||
 =1,
=1, =8
=8
2.11.
|
|
-5 |
-3 |
1 |
3 |
4 |
6 | ||||||
|
|
0,4 |
0,1 |
0,1 |
|
0,1 |
0,1 | ||||||
 =
-3,
=
-3, =4
=4
2.12.
|
|
-4 |
-2 |
3 |
5 |
7 | |||||
|
|
0,4 |
0,1 |
0,1 |
|
0,2 | |||||
 =
-2,
=
-2, =7
=7
2.13.
|
|
-10 |
-7 |
-1 |
2 |
4 | |||||
|
|
0,2 |
0,3 |
|
0,1 |
0,1 | |||||
 =
1,
=
1, =8
=8
2.14.
|
|
4 |
6 |
7 |
9 |
12 | |||||
|
|
0,3 |
0,2 |
|
0,1 |
0,1 | |||||
 =
6,
=
6, =9
=9
2.15.
|
|
2 |
3 |
8 |
10 |
14 |
15 | ||||||
|
|
|
0,1 |
0,2 |
0,2 |
0,1 |
0,1 | ||||||
 =
8,
=
8,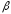 =15
=15
2.16.
|
|
4 |
5 |
7 |
9 |
16 | |||||
|
|
0,2 |
|
0,1 |
0,1 |
0,2 | |||||
 =
5,
=
5, =16
=16
2.17.
|
|
-8 |
-2 |
1 |
4 |
8 | |||||
|
|
|
0,2 |
0,3 |
0,1 |
0,1 | |||||
 =
1,
=
1, =8
=8
2.18.
|
|
-1 |
0 |
4 |
7 |
9 |
13 | ||||||
|
|
0,2 |
|
0,1 |
0,1 |
0,2 |
0,1 | ||||||
 =
0,
=
0, =9
=9
2.19.
|
|
-1 |
4 |
5 |
10 |
15 | |||||
|
|
0,1 |
|
0,2 |
0,3 |
0,1 | |||||
 =
4,
=
4, =15
=15
2.20.
|
|
2 |
10 |
17 |
19 |
24 |
28 | ||||||
|
|
0,2 |
0,1 |
|
0,1 |
0,2 |
0,1 | ||||||
 =
10,
=
10, =24
=24
Тема 3. Графический метод решения задачи линейного программирования
Линейным программированием называется область математики, занимающаяся решением экстремальных задач функции нескольких переменных при условии линейности функции и связей между переменными. Методы линейного программирования применяются для решения практических задач, в которых:
необходимо среди множества решений выбрать оптимальное;
ограничения, накладываемые на переменные, выражаются линейными уравнениями или неравенствами;
цель выражается в виде линейной функции нескольких переменных.
Для практического решения экономической задачи математическими методами необходимо записать ее с помощью математических выражений, т.е. составить экономико-математическую модель.
Общая задача линейного программирования
Общая задача линейного программирования имеет вид:
 (1)
(1)
 (2)
(2)
 (3)
(3)
Система mлинейных уравнений и неравенств сnнеизвестными (1) называетсясистемой ограничений; условие (2) —условием неотрицательности переменных, оно вытекает из экономического смысла вводимых переменных.
Если система ограничений (1) содержит линейные неравенства и уравнения, то задача называется общей,если только уравнения —основной. Частным случаем основной задачи является задачаканоническая, определение которой будет дано ниже. Любая задача линейного программирования (ЛП) может быть записана в одной из трех форм: общей, основной или канонической.
Вектор
 ,
удовлетворяющий системе ограничений
(1) и условию неотрицательности (2),
называетсяпланомзадачи.
,
удовлетворяющий системе ограничений
(1) и условию неотрицательности (2),
называетсяпланомзадачи.
Оптимальным называется такой план ,
при котором линейная функция (3) принимает
оптимальное (максимальное или минимальное)
значение, т.е.
,
при котором линейная функция (3) принимает
оптимальное (максимальное или минимальное)
значение, т.е.
 для
для ;
; для
для .
.
Функция
 называетсяцелевой функцией.
называетсяцелевой функцией.
Решение задачи ЛПзаключается в
нахождении оптимального планаХ*и вычислении значения целевой функции
на этом плане .
.
В случае, когда система ограничений общей задачи (1) содержит неравенства, связывающие только две переменные, задача допускает наглядный графический способ решения.
При n =2 задача ЛП имеет вид:
 (4)
(4)
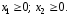 (5)
(5)
 (6)
(6)
Каждое линейное неравенство системы
(4) на плоскости
 определяет полуплоскость с границей,
задаваемой прямой
определяет полуплоскость с границей,
задаваемой прямой ;
условия неотрицательности (5) определяют
две полуплоскости с границами
;
условия неотрицательности (5) определяют
две полуплоскости с границами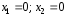 .
.
Если система (4)—(5) совместна, то пересечение полуплоскостей образует выпуклый многоугольник, внутренние и граничные точки которого образуют множество планов. (Напомним, что область называется выпуклой, если она полностью включает в себя отрезок, соединяющий любые две точки области). Этот многоугольник может быть ограниченным или представлять собой бесконечную выпуклую область.
В случае несовместности системы (4)—(5) множество планов пусто.
Линейная функция
 является функцией двух переменных. Из
теории известно, что градиент функции
— вектор, координатами которого являются
частные производные
является функцией двух переменных. Из
теории известно, что градиент функции
— вектор, координатами которого являются
частные производные ,
т.е.
,
т.е.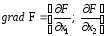 — в каждой точке перпендикулярен линии
уровня
— в каждой точке перпендикулярен линии
уровня и указывает направление наискорейшего
возрастания функции.
и указывает направление наискорейшего
возрастания функции.
Линиями уровня является множество
параллельных прямых
 =С(гдеС— произвольная постоянная);
векторgrad F=
=С(гдеС— произвольная постоянная);
векторgrad F= перпендикулярен к ним и направлен в
сторону наибольшего возрастания функции.
перпендикулярен к ним и направлен в
сторону наибольшего возрастания функции.
Решение задачи (4) — (5) сводится к отысканию
такой точки Х*области
планов, через которую проходит та из
прямых ,
которая соответствует наибольшему
(наименьшему) значению функции
,
которая соответствует наибольшему
(наименьшему) значению функции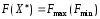 .
.
Построив прямую
 ,
параллельным переносом ее перемещают
по области планов в направлении grad
F, если
,
параллельным переносом ее перемещают
по области планов в направлении grad
F, если или в противоположном направлении, если
или в противоположном направлении, если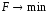 .
.
Оптимальное значение целевая функция принимает в угловых точках (или на соединяющем их отрезке) многоугольника планов. Это свойство решений является фундаментальным при решении задачи ЛП.
Для нахождения координат точки, в которой целевая функция оптимальна, сначала по чертежу определяют те прямые, пересечением которых является данная точка. Затем из уравнений этих прямых составляется система уравнений, решение которой дает координаты точки.
Пример.Решить задачу ЛП:

 .
.
 .
.
Поскольку задача содержит 2 переменные, решение можно найти графически.
Построим область планов задачи, определяемую системой ограничений и условиями неотрицательности переменных. Каждое из неравенств определяет полуплоскость с границей, задаваемой прямой. Выпишем соответствующие уравнения прямых, пронумеруем их. Прямую однозначно можно провести через любые две точки, в качестве которых удобно выбирать точки пересечения с осями координат. Координаты первой точки получим при подстановке в уравнение х1=0, откуда легко вычисляется х2; координаты второй точки — при подстановке в уравнениех2=0, откуда находимх1.

Проведем по двум точкам прямые (1) — (4), прямые (5) и (6) совпадают с осями координат х2 их1 (рис.1).
Для того, чтобы определить, какая из двух полуплоскостей будет решением данного неравенства, нужно в любой из полуплоскостей выбрать пробную точку и подставить ее координаты в левую часть неравенства.
х2(5)
(2)



6 F(X*)=Fmin
А= X*

3
F(Х)=0
В=X*
(4)

F(Х*)=Fmax



-2 0 4 5
9 (6)х1
(3)
(1) 
-2
grad
F(X)
Рис.1.
. Для того, чтобы определить, какая из двух полуплоскостей будет решением данного неравенства, нужно в любой из полуплоскостей выбрать пробную точку и подставить ее координаты в левую часть неравенства Если получится верное неравенство, то содержащая пробную точку полуплоскость будет решением; если неравенство не выполняется, то решением является полуплоскость, не включающая пробной точки. Если прямая не проходит через начало координат, то в качестве пробной удобно брать точку (0;0).
Подставим в первое неравенство х1=0
их2=0, получим неравенство .
Это верно, следовательно, начало координат
— точка (0;0) — принадлежит полуплоскости
решений; помечаем стрелками нижнюю от
прямой (1) полуплоскость.
.
Это верно, следовательно, начало координат
— точка (0;0) — принадлежит полуплоскости
решений; помечаем стрелками нижнюю от
прямой (1) полуплоскость.
При подстановке точки (0;0) во второе
неравенство получаем: 0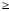 –8.
Это верно, поэтому помечаем полуплоскость,
содержащую начало координат.
–8.
Это верно, поэтому помечаем полуплоскость,
содержащую начало координат.
Для третьего неравенства при подстановке
координат пробной точки получаем
неверное утверждение 0 12,
следовательно, решением данного
неравенства будет полуплоскость, не
включающая начало координат.
12,
следовательно, решением данного
неравенства будет полуплоскость, не
включающая начало координат.
Подстановка координат точки (0;0) в
четвертое неравенство приводит к верному
неравенству 0 10;
решение содержит начало координат.
10;
решение содержит начало координат.
Условия неотрицательности определяют полуплоскости справа от прямой х2=0 и вверх от прямойх1=0.
Областью планов является заштрихованный пятиугольник — пересечение всех шести полуплоскостей.
Найдем максимальное и минимальное
значения целевой функции на области
планов. Рассмотрим произвольную линию
уровня, например,
 .
Прямую
.
Прямую построим по точкам (0;0) и (3;1). Направление
наискорейшего возрастания указывает
векторgrad F(X)=(1;–3).
построим по точкам (0;0) и (3;1). Направление
наискорейшего возрастания указывает
векторgrad F(X)=(1;–3).
Для определения максимума целевой
функции на области планов нужно
параллельным переносом сдвигать прямую
 в направлении grad
F(X).
По рисунку можно определить, что целевая
функция максимальна в точкеВ, т.е.Fmax=F(X*)=F(B).
ТочкаВобразована пересечением
прямых (4) и (6); ее координатыВ(5;0). На
оптимальном планеХ*=(5;0)
достигаетсяFmax=F(X*)=
в направлении grad
F(X).
По рисунку можно определить, что целевая
функция максимальна в точкеВ, т.е.Fmax=F(X*)=F(B).
ТочкаВобразована пересечением
прямых (4) и (6); ее координатыВ(5;0). На
оптимальном планеХ*=(5;0)
достигаетсяFmax=F(X*)= =5.
=5.
Для определения наименьшего
значения на области планов нужно параллельным
переносом сдвигать прямую
на области планов нужно параллельным
переносом сдвигать прямую в направлении, противоположномgrad
F(X).
Наименьшее значение целевой функции
достигается в точкеА, являющейся
пересечением прямых (1) и (2), т.е.
Fmin=F(X*)=F(A). Координаты точкиАнайдем, решив
систему уравнений:
в направлении, противоположномgrad
F(X).
Наименьшее значение целевой функции
достигается в точкеА, являющейся
пересечением прямых (1) и (2), т.е.
Fmin=F(X*)=F(A). Координаты точкиАнайдем, решив
систему уравнений:

Умножим первое уравнение на 2 и вычтем из него второе:
11х2= 44,х2= 4. Тогдах1=1/2(18 – 12)= 3. Координаты точкиА(3;4). Оптимальным является план
Х*=(3;4), на котором оптимальное
значение целевой функцииFmin=F(X*)=F(A)=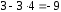 .
.
Если количество переменных системы (1.1)—(1.2.) больше двух, задача не допускает наглядного графического решения.