
- •Математика
- •Санкт-Петербург
- •Содержание
- •2. Методические указания к изучению дисциплины
- •3. Методические указания к выполнению контрольной работы
- •Контрольная работа №1
- •Тема 1. Решение матричных уравнений
- •Каждой квадратной матрице ставится в соответствие число
- •Пример1. Найти а-1 , если.
- •Пример2.
- •Тема 2. Решение систем линейных уравнений
- •Контрольные задания
- •Тема 3. Основы дифференциального исчисления
- •Контрольные задания
- •Тема 4. Функции двух переменных
- •Контрольные задания
- •Тема 5. Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования Непосредственное интегрирование
- •Замена переменой в неопределенном интеграле
- •Интегрирование по частям в неопределенном интеграле
- •Интегрирование рациональных дробей
- •Контрольные задания
- •Тема 6. Определенный интеграл
- •Контрольные задания
- •Тема 7. Дифференциальные уравнения
- •Уравнение с разделяющимися переменными
- •Однородное уравнение первого порядка
- •Линейное уравнение первого порядка
- •Контрольные задания
- •Тема 8. Ряды Рассмотрим выражение вида ,(1)
- •Контрольные задания
- •Контрольная работа №2
- •Тема 1. Случайные события
- •Контрольные задания
- •Тема 2. Случайные величины
- •Контрольные задания
- •Тема 3. Графический метод решения задачи линейного программирования
- •Контрольные задания
- •Тема 4. Симплекс-метод решения задачи линейного программирования
- •Контрольные задания
- •Тема 5. Транспортная задача
- •Контрольные задания
- •5. Требования к выполнению контрольной работы
- •6.1 Основная литература
- •6.1 Дополнительная литература
- •Содержание дисциплины
- •Тема 1.5. Дифференциальное исчисление функции нескольких переменных
- •Тема 3.2. Системы обыкновенных дифференциальных уравнений.
- •Образец оформления титульного листа
Контрольные задания
Определить область сходимости ряда.
8.1.
 .
.
8.2.
 .
.
8.3.
 .
.
8.4.
 .
.
8.5.
 .
.
8.6.
 .
.
8.7.
 .
.
8.8.
 .
.
8.9.
 .
.
8.10. .
.
8.11. .
.
8.12. .
.
8.13. .
.
8.14.
8.15. .
.
8.16.
8.17.
8.18. .
.
8.19. .
.
8.20.
Контрольная работа №2
Тема 1. Случайные события
Основным понятием теории вероятности является понятие случайного события.
Случайнымназывается такое событие, которое может произойти или не произойти в результате данного опыта. Например, выпадение орла при бросании монеты — случайное событие.
Обозначим множество элементарных
событий
 через
через .
Любое подмножество
.
Любое подмножество множества
множества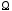 называетсясобытием.
называетсясобытием.
Событие
 наступает тогда, когда результатом
опыта является одно из элементарных
событий, входящих в
наступает тогда, когда результатом
опыта является одно из элементарных
событий, входящих в .
.
Пример
1.Пусть событие заключается в выпадении четного числа
очков при однократном бросании игральной
кости. Тогда элементарные события
заключается в выпадении четного числа
очков при однократном бросании игральной
кости. Тогда элементарные события .
Событие
.
Событие .
.
Суммой событий называется событие, состоящее из тех
элементарных событий, которые входят
или в событие
называется событие, состоящее из тех
элементарных событий, которые входят
или в событие или в событие
или в событие ,
или в то и в другое. Суммой является
событие, состоящее в появлении хотя бы
одного из этих событий.
,
или в то и в другое. Суммой является
событие, состоящее в появлении хотя бы
одного из этих событий.
Пример
2.Есть два лотерейных билета. Пусть
событие — выигрыш по первому, событие
— выигрыш по первому, событие — выигрыш по второму билету. Тогда
— выигрыш по второму билету. Тогда есть выигрыш по одному из билетов или
по обоим сразу.
есть выигрыш по одному из билетов или
по обоим сразу.
Произведениемсобытий называется событие, состоящее из тех
элементарных событий, которые входят
в оба события. Т.е. это событие состоит
в осуществлении одновременно этих двух
событий.
называется событие, состоящее из тех
элементарных событий, которые входят
в оба события. Т.е. это событие состоит
в осуществлении одновременно этих двух
событий.
Событие является достоверным, если оно неизбежно произойдет в условиях данного опыта.
Пустое множество
 называетсяневозможным событием.Невозможным является событие, появление
которого в условиях данного опыта
исключается.
называетсяневозможным событием.Невозможным является событие, появление
которого в условиях данного опыта
исключается.
События
 и
и называютнесовместными, если
называютнесовместными, если .
Т.е. два события несовместны, если
появление одного исключает появление
другого и наоборот.
.
Т.е. два события несовместны, если
появление одного исключает появление
другого и наоборот.
Пример
3.Игральную кость бросают один раз.
Пусть событие — появление четного,
— появление четного, — нечетного числа очков. События
— нечетного числа очков. События и
и несовместны.
несовместны.
Событие
 называютпротивоположнымсобытию
называютпротивоположнымсобытию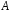 ,
если
,
если и
и .
.
События
 и
и называютэквивалентными, если
называютэквивалентными, если .
.
События
 образуютполную группу событий, если
они попарно несовместны и их сумма равна
достоверному событию, т.е. если
образуютполную группу событий, если
они попарно несовместны и их сумма равна
достоверному событию, т.е. если и
и .
.
Например, при однократном броске
игральной кости события
 ,
заключающиеся в выпаденииi-го
числа очков (i=1, 2, 3, 4,
5, 6), образуют полную группу.
,
заключающиеся в выпаденииi-го
числа очков (i=1, 2, 3, 4,
5, 6), образуют полную группу.
Классическое определение вероятности
Вероятность события
 —
это численная мера объективной возможности
его появления.
—
это численная мера объективной возможности
его появления.
Если, в частности, множество всех
элементарных событий
 состоит из
состоит из равновозможных событий (т.е.
равновозможных событий (т.е. событий образуют полную группу), то
вероятность события
событий образуют полную группу), то
вероятность события равна числу
равна числу элементарных событий, входящих
элементарных событий, входящих ,
деленному на число всех событий, т.е.
,
деленному на число всех событий, т.е.
 .
(1)
.
(1)
Случай равновозможных событий называется классическим, поэтому и формула (1) называется классическим определением вероятности.
Элементарные события (исходы опыта),
входящие в событие
 ,
называютсяблагоприятными.
,
называютсяблагоприятными.
Из определения вероятности вытекают следующие свойства:
1. Вероятность невозможного события равна нулю.
2.Вероятность достоверного события равна единице.
3. Вероятность любого события есть
неотрицательное число, не превосходящее
единицу:
 .
.
4. Эквивалентные события имеют одинаковую вероятность.
5.
 ,
если
,
если .
.
При вычислении общего числа исходов опыта nи числа исходовm, благоприятных событиюА, часто бывает необходимо пользоваться понятиями и формулами комбинаторики. Напомним основные из них.
Основная теорема комбинаторики.
Пусть естьkдействий,
осуществляемых одно за другим. Пусть
1-ое действие можно осуществить числом способов, 2-ое —
числом способов, 2-ое — ,
...,
,
..., -ое—
числом
-ое—
числом .
Тогда общее число
.
Тогда общее число действий можно выполнить
действий можно выполнить способами.
способами.
Пример 4.Сколькими способами можно из цифр 0,1,2,3,4 составить различные двузначные четные числа?
Чтобы число было четным, разряд единиц
можно заполнить тремя способами; чтобы
оно было двузначным, есть 4 варианта
заполнения разряда десятков. Общее
число способов составления двузначного
четного числа
 .
.
Перестановкойиз элементов называется любое упорядоченное
множество, в которое входят по одному
разу все
элементов называется любое упорядоченное
множество, в которое входят по одному
разу все различных элементов данного множества.
Число перестановок
различных элементов данного множества.
Число перестановок различных элементов обозначается
различных элементов обозначается и вычисляется по формуле:
и вычисляется по формуле:
 .
.
( Знак «!» читается как «факториал», по определению считается 0!=1.)
Пример 5.Сколькими способами можно составить различные пятизначные числа из цифр 1,2,3,4,5 без повторения?
Перестановкой пяти цифр можно составить
 =5!=
=5!= пятизначных чисел.
пятизначных чисел.
Размещением из
 элементов по
элементов по называется любоеупорядоченноеподмножество из
называется любоеупорядоченноеподмножество из элементов множества, состоящего из
элементов множества, состоящего из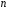 различных элементов, и обозначается
различных элементов, и обозначается .
Размещения отличаются либо составом,
либо порядком элементов. Число размещений
из
.
Размещения отличаются либо составом,
либо порядком элементов. Число размещений
из
 элементов по
элементов по
 обозначается
обозначается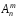 и вычисляется по формуле:
и вычисляется по формуле:
 .
.
Пример 6.Сколькими способами можно выбрать старосту, профорга и культорга из группы 25 человек?
Перестановки по должностям внутри группы выбранных трех человек дают разные наборы, поэтому ответом на вопрос будет число размещений

 .
.
Сочетанием из
 элементов по
элементов по называетсялюбоеподмножество из
называетсялюбоеподмножество из элементов, которые принадлежат множеству,
состоящему из
элементов, которые принадлежат множеству,
состоящему из различных элементов. Различные сочетания
отличаются друг от друга только составом
элементов. Число сочетаний обозначается
различных элементов. Различные сочетания
отличаются друг от друга только составом
элементов. Число сочетаний обозначается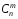 и вычисляется по формуле:
и вычисляется по формуле:
 .
.
Пример 7.Сколькими способами можно выбрать трех делегатов конференции из группы 25 человек?
Необходимо выбрать из 25 человек группы
по 3 человека, эти группы отличаются
друг от друга только составом (все
«должности» внутри группы одинаковы),
поэтому будем считать число сочетаний

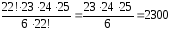 .
.
Теперь вернемся к определению классической вероятности события А, вычисляемой по формуле (1).
Пример 8.Найти вероятность того, что при бросании трех монет выпадет ровно 2 орла.
Пусть событие А— выпадение 2 орлов.
Подсчитаем общее число исходов опытаn. Каждая монета может
лечь либо орлом (О), либо решкой (Р), т.е.
имеется две возможности. По основной
теореме комбинаторики общее число
исходов .
Событиями, благоприятными событиюА,
являются комбинации ООР, ОРО, РОО,
.
Событиями, благоприятными событиюА,
являются комбинации ООР, ОРО, РОО, =3.
Вероятность того, что при бросании трех
монет выпадет ровно 2 орла
=3.
Вероятность того, что при бросании трех
монет выпадет ровно 2 орла .
.
Пример 9.В классе 12 мальчиков и 10 девочек. На уроке опрошено четверо учеников. Какова вероятность того, что все они были мальчиками, если опрос любого ученика равновероятен?
Будем считать событием
 опрос четырех мальчиков. Выбрать четырех
человек из класса можно
опрос четырех мальчиков. Выбрать четырех
человек из класса можно =
= способами. Из них благоприятными событию
способами. Из них благоприятными событию являются
являются способов.
Следовательно,
способов.
Следовательно,
 .
.
Теоремы сложения вероятностей
Сформулируем основные теоремы.
Теорема 1. Вероятность суммы двухнесовместныхсобытий (т.е. )
определяется формулой:
)
определяется формулой:
 .
.
Следствие 1.Если случайные
события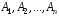 образуют полную группу несовместных
событий, то
образуют полную группу несовместных
событий, то .
.
Следствие 2.Сумма вероятностей противоположных событий равна единице:
 .
.
Пример 10.В урне находится 12 белых, 7 красных и 11 черных шаров. Извлекают 1 шар. Найти вероятность того, что он не белый.
Пусть событие
 заключается в извлечении из урны
красного, событие
заключается в извлечении из урны
красного, событие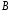 —черного шаров, событие С — извлечение
не белого шара. События
—черного шаров, событие С — извлечение
не белого шара. События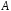 и
и несовместны,
несовместны, .
.
Эту задачу можно было решить, рассуждая
иначе. Если событие
 — извлечение из урны белого шара, то
противоположным ему является событие
— извлечение из урны белого шара, то
противоположным ему является событие — извлечение шара не белого цвета.
Поскольку
— извлечение шара не белого цвета.
Поскольку ,
то
,
то

 .
.
Теорема 2. Вероятность появления хотя бы одного из суммы двухсовместныхсобытий равна сумме вероятностей этих событий без вероятности их совместного наступления:
 .
.
Условная вероятность. Теоремы умножения вероятностей
Вероятность того, что произошло событие
 при условии, что
при условии, что произошло, называетсяусловной
вероятностьюсобытия
произошло, называетсяусловной
вероятностьюсобытия и обозначается
и обозначается или
или .
.
Теорема 3. Вероятность произведения двух событий равняется произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое произошло:
 .
.
Следствие. Для любых и
и справедлива формула
справедлива формула
 .
.
Пример 11.Студент знает 20 вопросов из 25. Какова вероятность того, что он правильно ответит на предложенные ему подряд 2 вопроса?
Пусть событие
 заключается в том, что студент знает
первый вопрос, событие
заключается в том, что студент знает
первый вопрос, событие — знает второй вопрос.
— знает второй вопрос.

 ,
, (т.к. после первого ответа осталось 24
вопроса, из которых студент знает 19).
Тогда вероятность того, что он знает
оба вопроса равна
(т.к. после первого ответа осталось 24
вопроса, из которых студент знает 19).
Тогда вероятность того, что он знает
оба вопроса равна
 =
=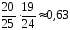 .
.
Два события называются независимыми, если появление любого из них не меняет вероятности появления другого, т.е.
 .
.
Теорема 4. Вероятность совместного
появления двух независимых событий
равна произведению их вероятностей: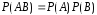 .
.
Пример
12.Вероятность того, что в течение
одной смены возникнет неполадка станка,
равна .
Какова вероятность того, что не произойдет
ни одной неполадки за три смены?
.
Какова вероятность того, что не произойдет
ни одной неполадки за три смены?
Пусть событие А— в первую смену
станок будет работать без неполадок, 1–0,05=0,95.
СобытияB иC— бесперебойная работа во вторую и
третью смены,
1–0,05=0,95.
СобытияB иC— бесперебойная работа во вторую и
третью смены,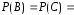 1-0,05=0,95.
Событие, заключающееся в том, что за три
смены не произойдет ни одной неполадки
станка, состоит в совместном наступлении
событийA,Bи C.СобытияA,Bи Cнезависимы,
поэтому
1-0,05=0,95.
Событие, заключающееся в том, что за три
смены не произойдет ни одной неполадки
станка, состоит в совместном наступлении
событийA,Bи C.СобытияA,Bи Cнезависимы,
поэтому
 .
.
Пример 13 .В одной урне 5 белых и 10 красных шаров, во второй — 10 белых и 5 красных. Найти вероятность того, что хотя бы из одного ящика был вынут белый шар, если из каждого извлечено по одному шару.
Пусть событие
 —
белый шар извлечен из первой урны,
событие
—
белый шар извлечен из первой урны,
событие — белый шар извлечен из второй. События
— белый шар извлечен из второй. События и
и совместны, поэтому
совместны, поэтому
 .
.
Формула полной вероятности
Теорема. Если событие может наступить только совместно с
появлением одного из событий
может наступить только совместно с
появлением одного из событий некоторой полной группы несовместных
событий
некоторой полной группы несовместных
событий (события этой группы называют гипотезами),
то вероятность события
(события этой группы называют гипотезами),
то вероятность события вычисляется по формуле полной вероятности
вычисляется по формуле полной вероятности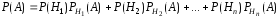 .
.
Или, кратко:

где
 — вероятность гипотезы
— вероятность гипотезы ,
, — условная вероятность события
— условная вероятность события при условии осуществленияi-ой гипотезы,
при условии осуществленияi-ой гипотезы, .
.
Пример 14.В урну, содержащую 2 шара, опущен белый шар, после чего наудачу извлечен 1 шар. Найти вероятность того, что он белый, если первоначальный состав шаров по цвету мог быть любым.
Пусть событие
 — извлечение белого шара. Рассмотрим
гипотезы о первоначальном составе шаров
в урне:
— извлечение белого шара. Рассмотрим
гипотезы о первоначальном составе шаров
в урне: ={в урне было
2 белых шара},
={в урне было
2 белых шара}, ={в урне был 1 белый шар},
={в урне был 1 белый шар}, ={в урне белых шаров не было}.
={в урне белых шаров не было}.
Гипотезы
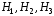 образуют полную группу событий, т.к. эти
события единственно возможны и попарно
несовместны,
образуют полную группу событий, т.к. эти
события единственно возможны и попарно
несовместны, .
.
В условиях неопределенности считаем,
что гипотезы
 равновозможны, поэтому
равновозможны, поэтому
 .
Рассмотрим вероятность извлечения
белого шара при реализации каждой из
гипотез:
.
Рассмотрим вероятность извлечения
белого шара при реализации каждой из
гипотез:

 =
=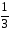 .
По формуле полной вероятности
.
По формуле полной вероятности
 .
.
Формула Байеса
Формула Байеса позволяет «пересмотреть» вероятности гипотез после того, как стало известно, что событие А наступило:
 ,
где
,
где — вероятность гипотезы
— вероятность гипотезы при условии, что событиеАпроизошло,
при условии, что событиеАпроизошло, —
вероятность гипотезы накануне испытания,
—
вероятность гипотезы накануне испытания, — вероятность событияАпри
осуществлении этой гипотезы,
— вероятность событияАпри
осуществлении этой гипотезы,
 —
полная вероятность.
—
полная вероятность.
Пример 15.В отдел технического контроля поступают детали из двух цехов. Производительность первого цеха вдвое больше, чем во втором. Процент бракованных изделий составляет для первого цеха 5%, для второго — 3%. Взятая на проверку деталь оказалась бракованной. Какова вероятность того, что она изготовлена в первом цехе?
Пусть событие А— выбранная деталь
бракованная, гипотеза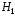 —
она изготовлена в первом цехе, гипотеза
—
она изготовлена в первом цехе, гипотеза —
во втором. Гипотезы
—
во втором. Гипотезы и
и образуют полную группу.
образуют полную группу. ,
, ,
, ,
, .
Найдем полную вероятность:
.
Найдем полную вероятность: .
Тогда
.
Тогда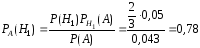 .
.
Независимые испытания. Формула Бернулли
Пусть проводится nповторных независимых испытаний (т.е. исход в каждом испытании не зависит от исходов в других испытаниях), вероятность появления событияА в каждом из них неизменна и равнаp. Тогда вероятность того, что вnиспытаниях событиеАпоявится ровно mраз, определяется формулой Бернулли:
 ,
где
,
где .
.
Пример 16.Игральную кость бросают 5 раз. Какова вероятность того, что не менее четырех раз выпадет цифра 6?
Событие Азаключается в выпадении
цифры 6, в каждом испытании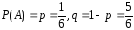 .
Условие того, что цифра 6 выпадет не
менее 4 раз означает, что она выпадет 4
или 5 раз.
.
Условие того, что цифра 6 выпадет не
менее 4 раз означает, что она выпадет 4
или 5 раз.
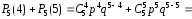

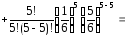
 .
.
