2012nmi_book

Решения и ответы олимпиады по алгебре

1.Поскольку ¡2 является корнем P (x) = x3 + 507x2 + 2016x + 2012; то по теореме Безу P (x) = (x + 2)Q(x): Частное Q(x) = x2 + 505x + 1006

легко найти с помощью деления уголком. Далее легко найти корни p

Q(x) по формуле ¡b § b2 ¡ 4ac:

2a

Ответ: ¡2 корень кратности два, ¡503:

Критерии оценивания: за каждый найденный корень 1 балл.

полное решение (найдены все корни, указаны кратности корней, из решения следует, что других корней нет) 7 баллов.

полное решение, но не указана кратность корня x = 2 6 баллов.

Замечание 1. Поскольку 2012 = 22 ¢ 503; то целыми корнями многочлена P (x) могут быть только числа §1; §2; §4; §503; §1006; §2012:

Замечание 2. Дискриминант равен 251001. Поскольку 5002 » 251001; то легко догадаться p251001 = 501:

2.Пусть x стоимость супа, y стоимость второго, z стоимость салата, t стоимость сырка. Перепишем условие задачи в виде ра-

Критерии оценивания: полное решение с арифметической ошибкой в конце решения 6 баллов.

Замечание 1. Можно было решить систему уравнений стандратно – привести к ступенчатому виду, выразить переменные через свободную переменную, и, затем, решение подставить в 2x + 2y + t:

3. (cos 72± + i sin 72±)5 = cos 360± + i sin 360± = 1 по формуле Муавра (cos ' + i sin ')n = cos n' + i sin n': Поэтому w = cos 72± + i sin 72±

где fa; b; cg = f13; 15; 17g: Заметим, что c = 45 ¡ a ¡ b и потери общ-

ности нет. Выпишем общее решение этой системы: k = ¡2a ¡ b + n;

3

m = ¡a ¡ 2b + n: Из перебора трёх случаев a = 13; b = 15; a = 13; b = 3

17; a = 15; b = 17 следует, что система не имеет целых решений. Следовательно, хамелеоны все не могут стать одного цвета.

Решение 2. Пусть (ai; bi; ci) количество хамелеонов на i-м шаге. Рассмотрим сумму модулей разностей между количествами хамелеонов

I = jai ¡ bij + jai ¡ cij + jbi ¡ cij. При встрече любых двух хамелеонов каждое слагаемое либо не изменится, либо изменится на 3. В начале

выражение I не кратно 3. В случае одноцветных хамелеонов I = 45 и кратно 3. Следовательно, хамелеоны все не могут стать одного цвета.

Замечание. Остаток I от деления на 3 называется инвариантом данного процесса превращений хамелеонов.

Решения и ответы олимпиады по матем. анализу, 1 курс

1.Пусть x1 = 1 + p3 и x2 корни многочлена x2 + ax + b: Тогда из равенства x2 + ax + b = (x ¡ x1)(x ¡ x2) следует

Избавимся от переменной x2; выразив ее через b: Действительно,

b (1 ¡ p3)b 1 p3 x2 = 1 + p3 = (1 + p3)(1 ¡ p3) = ¡2b + 2 b:

2.Используя тождества cos2 x+sin2 x = 1 и cos 2x = cos2 x¡sin2 x; алгеб-

раическими преобразованиями полученных интегралов легко вывести, что эти интегралы отличаются на постоянные. Второй интеграл больше первого на 1/2, третий на 1/4. Ответ: Все трое правы.

3.Докажем от противного. Допустим мы нашли такой многочлен P (x) и такую точку (a; b); что из нее можно провести как минимум n + 1 касательную к графику многочлена P (x): Пусть абциссы точек касания касательных x1; x2; . . . , xn+1: Тогда уравнения этих касательных

гуры пополам. Пусть x1 и x2 абсциссы точек пересечения графиков функций f(x) и g(x):

С другой стороны, f(x) ¡ g(x) = ¡3x2 ¡ px ¡ q является параболой с корнями x1 и x2: Следовательно, осью симметрии параболы является

прямая x = 12(x1 + x2); где по теореме Виета x1 + x2 = ¡p3:

Ответ: x = ¡p6:

5.В преобразованиях ряда воспользуемся тождеством 4 sin3 y = 14(3 sin y¡

Решения и ответы олимпиады по математической логике

1.Все трое не могут быть Рыцарями, поэтому первый и второй Лжецы. Следовательно, третий сказал правду, поэтому он Рыцарь.

Стандартное решение. Всего существует 23 = 8 вариантов: РРР,

РРЛ, РЛР, ЛРР, РЛЛ, ЛРЛ, ЛЛР, ЛЛЛ. Перебором легко установим единственный возможный вариант.

Ответ: первый и второй Лжецы, третий Рыцарь.

2.Если C ложна, то данная формула © = (: : :) ^ C ложна. Если B и C истинны, то © = ((: : :)_B)^C истинна. Осталось рассмотреть случаи когда A произвольная, B ложна, C истинна. В этом случае A _ B = A; тогда (A _ B) ^ C = A; поэтому © = A: Составим таблицу истинности

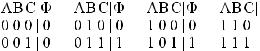
Такую же таблицу истинности имеет формула (A _ B) ^ C:

Ответ: (A _ B) ^ C:

3.Формула A2012 _ :A1 эквивалентна формуле A1 ! A2012:

4.Истинность высказывания A ^B ^C означает истинность каждого из

высказываний A; B и C: Истинность A1 _ A1 _ : : : _ A7 означает, что хотя бы один из A1; A2; . . . , A7 является истинным.

Таким образом, истинность данного высказывания равносильно высказыванию "среди семи выбранных шаров есть хотя бы один белый шар, хотя бы один красный и хотя бы один синий шар".

Перекрасим шары следующим образом: самые многочисленные белым, малочисленные синим, остальные красным. Ясно, что если n > 10; то суммарное количество белых и красных шаров будет не менее 7. Тогда при выборе именно 7 красных и белых данное высказывание будет ложным там не будет синих.

Следовательно, осталось проверить истинность формулы при n = 8: Если имеется 3 белых, 3 красных и 2 белых шара, то никакие два цвета в сумме не дают 7. Следовательно, любой набор из 7 шаров будет содержать все цвета.

5.(a) Для x1 прямоугольника со сторонами 1 и 2 A(x1) ложно, E(x1) истинно, поэтому 8x(A(x) ! E(x)) имеет контрпример x1:

(b)Трапеция x2 с вершинами в точках (0; 0); (3; 4); (8; 4); (11; 0) имеет три равные стороны длины 5. Поэтому 9x(A(x) ! F (x)) верно.

(c)Достаточно доказать, что из существования 4 пар равных элементов среди 4 элементов следует равенство всех этих элементов. Это очевидно, поскольку среди 3 элементов существует всего 2 + 1 = 3 различные пары.

6.Ответ: Ваня любит чай, занимается борьбой и учиться на третьем курсе. Коля любит пепси, занимается боксом и учится на втором. Ньургун любит кофе, занимается бегом и учится на первом курсе.

озамеченных ошибках, пожалуйста, сообщите на eshamaev@mail.ru