1.7. Силу реакции Naопределим рассмотрев одно из двух условий равновесия балки – условие равенства нулю суммы моментов всех приложенных к заготовке сил.

В качестве точки относительно, которой подсчитываются моменты сил удобно взять точку В. Через эту точку проходит линия действия силы реакции N_b и её момент окажется равным нулю. Условие равновесия: . Откуда: . Ответ:.

1.8.

Сечение с координатой х находится слева от точки приложения силы F, поэтому поперечная сила Q в этом сечении равна силе реакции опоры в точке А ( N_a). Силу реакции N_a определим, рассмотрев одно из двух условий равновесия балки – условие равенства нулю суммы моментов всех приложенных к заготовке сил. В качестве точки относительно, которой подсчитываются моменты сил удобно взять точку В. Через эту точку проходит линия действия силы реакции N_b и её момент окажется равным нулю. Условие равновесия:

. Откуда: .

Ответ: .

1.9.

Изгибающий моментM(x) в сечении с координатой, превышающей координату точки приложения сосредоточенной силы F, рассчитывается по формуле: .

На рисунке показана диаграмма (эпюра) изгибающего момента.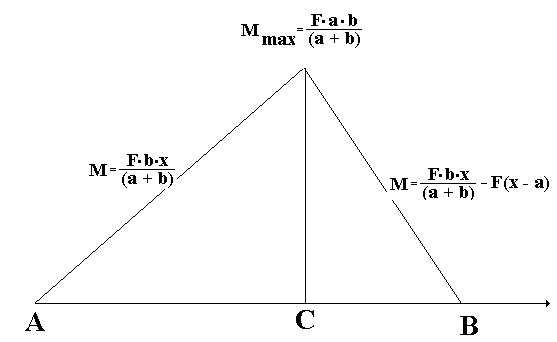

Подставляя числовые данные, получим ответ:

.

1.10.

Максимальный изгибающий момент M_max приходится на сечение с координатой в точке С и рассчитывается по формуле:

.

Подставляя числовые данные, получим ответ:

.

1.11. Связь модуля сдвига (g), модуля Юнга (e) и коэффициента Пуассона (μ) определяется формулой:.

Подставляя числовые данные, получим ответ:

.

1.12. Связь модуля сдвига (g), модуля Юнга (e) и коэффициента Пуассона (μ) определяется формулой:.

Подставляя числовые данные, получим ответ:

.

1.13. По определению коэффициент Пуассона (μ) есть взятое со знаком минус отношение поперечной относительной деформации к продольной относительной деформации. Для случая цилиндрического образца: . Числитель этой формулы при растяжении образца оказывается отрицательным. Подставляя числовые данные, получим ответ:

1.14. По определению коэффициент Пуассона: , где - относительна поперечная, а - относительная поперечная деформации. Поперечные деформации будут наименьшими, когда они равны нулю и = 0, при этом коэффициент Пуассона окажется равным нулю.

. Коэффициентом Пуассона равным нулю обладают пористые материалы, например пробка. Такие материалы не могут использоваться в качестве пломбировочных материалов в стоматологии. Наилучшим материалом в смысле соотношения коэффициентов Пуассона будет тот, у которого окажется наименьшим . Ответ: 2.

1.15. При стандартном (ГОСТ 9012 – 59) измерении твёрдости по Бринеллю стальной шарик диаметром D вдавливают в испытуемый образец под приложенной определённое время нагрузкой P; после снятия нагрузки измеряют диаметр d оставшегося на поверхности образца отпечатка. Ответ: 1.

1.16. Число твёрдости по Бринеллю (HB МПа) есть отношение нагрузки P = 30 кН при времени выдержки τ = 10 с, действующей на шаровой индентор диаметромD = 10мм, к площади F(м²) шаровой поверхности отпечатка:(МПа). Откуда: . Подставив числовые данные, получим ответ: .

1.17. При стандартном измерении твёрдости по Виккерсу (ГСТ 2999-75) в поверхность образца вдавливают алмазный индентор в форме четырёхгранной пирамиды с углом при вершине α . После удаления нагрузки, действовавший определённое время (1015с), измеряют диагональ отпечатка d, оставшегося на поверхности образца.

Число твёрдостиHV определяют делением нагрузкиP на площадь пирамидального отпечаткаF. ; . Откуда: .

Подставив числовые данные, получим ответ

м

1.18. Как видно из графика, при 350^оК предел текучести меньше, чем предел хрупкой прочности.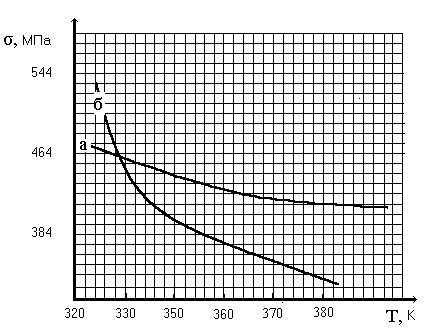Следовательно, разрушение при 350^оК оказывается пластическим. Ответ: разрушение пластическое.

1.19. Как видно из графика,

при достижении напряжения 64 МПа оно не изменяется в некотором диапазоне деформаций, поэтому предел текучести в данном случае и составляет 64 МПа. Ответ: предел текучести составляет 64 МПа.

1.20. В согласии с определением коэффициента запаса прочности, допустимое напряжение в 'опасном' сечении должно быть меньше предела прочности, делённого на коэффициент запаса прочности.

Ответ: допустимое напряжение в данном случае и составляет 196/3 МПа ≈ 65,3 МПа.

1.21. При одной и той же температуре долговечность меньше при большем напряжении. Напряжению 0,2 ГПа на графике соответствует самая крутая кривая. . Точка пересечения прямой при 0,2 ГПа с вертикальной линией, проходящей на графике через абсциссу даёт lg(t) = 5,3. Время, прошедшее до разрушения образца, находящегося под напряжением 0,2 ГПа и температуре 49,6 градуса по Цельсию составляет 10^5,3с.

Ответ: Время, прошедшее до разрушения образца, 10^5,3с.