3.7.3. Нейронные сети
Искусственные Нейро-Сети, или ANN, предлагают другое средство для сегментации респондентов. Архитектура Кохоненна это самоорганизующаяся ANN, которая может быть использована для сегментации. Она названа самоорганизующейся, поскольку, как и в кластерном анализе, в модели нет установленных зависимых переменных. ANN пытается сгруппировать респондентов базируясь на их похожих элементах. Она отличается от кластерного анализа своей способностью игнорировать “шумные” данные. Атипичные индивидуумы имеют меньше влияния на расчет сегментации и каждая успешная итерация делает все меньшие изменения весу в сети, так что расчеты быстро стабилизируются игнорируя нечастые характеристики респондентов. Чем больше вариация или неуверенность в ответах респондентов, тем лучше по сравнению с кластерным анализом работает ANN.
3.7.4. Структуры латентных классов
Анализ латентных классов часто описывается как ”факторный анализ для категорийных переменных”. Он используется для нахождения скрытых конструкций внутри множества переменных. Однако, анализ латентных классов тоже может быть использован для кластеризации категорийных переменных в сегменты базирующиеся на ответах широкого поля категорийных переменных. Латентные классы пытаются найти скрытые конструкции которые мотивируют людей на покупку определенного продукта или их желание определенных особенностей в продукте.
3.8. Классификационные алгоритмы
Есть несколько классификационных алгоритмов или аналитических методов, которые можно применить к сегментации рынка. Дискриминантный анализ может быть использован для классификации респондентов в предопределенные сегменты, базирующиеся на описательных переменных, таких как данные ценза. Схема сегментации определяет какие респонденты принадлежат к каждому сегменту рынка. Программа классификации или измерения затем создает средние потенциальных идентификационных членов каждого сегмента базирующееся на ограниченной информации(обычно данных которые могут быть получены из вторичных источников). Когда ограниченный набор информации может быть использован для точного предсказания к какому сегменту маркетинга принадлежит каждый индивидуум, вы получили удачный алгоритм классификации. Множественная регрессия и мультиноминальный логит могут быть использованы в той же манере для получения схем классификации для вашего сегмента рынка.
3.9. Количество сегментов
К несчастью, нет определенного ответа. Опыт, интуиция, статистические результаты и здравый смысл, все это нужно применять для того, чтобы решить сколько сегментов выделить. Если у вас слишком маленькие сегменты, вам может быть нужным изменить критерии сегментации или убрать некоторых респондентов как ”выброс”. Слишком большое количество сегментов может привести к разработке множества разных маркетинговых программ для маленьких, очень маленьких рынков.
Вот несколько основных правил для сегментации:
Достаточно большие. Основная часть сегментов должна быть достаточно большой чтобы было экономически осмысленным нацеливать на нее маркетинг и разработку продукта.
Уместны. Сегменты должны быть подходящими для продукта/услуги вашей компании.
Достижимые. Сегменты должны быть достижимы при помощи одной или нескольких смешанных маркетинговых переменных(цена, промоушен, особенности или распространение).
Различные. Должны быть четко определены различия между сегментами рынка чтобы сделать некоторые сегменты предпочтительнее других. Если много сегментов хотят в основном одинаковые особенности и намеренны покупать с одинаковой частотой и на одинаковом уровне, тогда эти сегменты не демонстрируют значимых различий.
3.10. Методика расчёта сегментации рынка
Процесс расчета сегментации рынка можно разделить на два этапа:
определение близости объектов;
систематизация полученных результатов.
В данной методике на первом этапе используются элементы кластерного анализа, и на следующем этапе результаты систематизируются с помощью диаграмм Чекановского.
Исходным шагом, предопределяющим правильность конечных результатов, является формирование матрицы наблюдений. Эта матрица содержит наиболее полную характеристику изучаемого множества объектов и имеет вид:
X=
где w - число объектов; n - число признаков; ik - значение признака k для объекта i.
На данном этапе мы не можем перейти непосредственно к процессу расчета расстояния между объектами, по причине того, что признаки измерены в разнородных единицах измерения, и все значения необходимо нормировать. Нормирование представляет собой переход к некоторому единообразному описанию для всех признаков, к введению новой условной единицы измерения, допускающей формальные сопоставления объектов. Ниже приведены наиболее часто используемые методы нормировки.
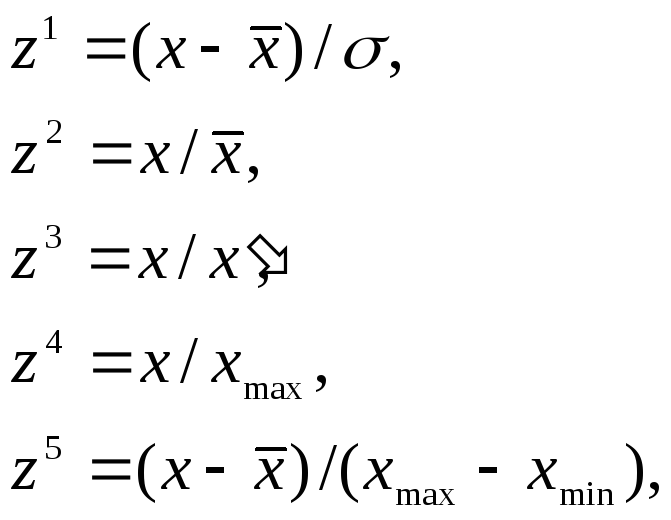
где
- соответственно среднее и среднеквадратическое
отклонениеx,
-
некоторое
эталонное (нормативное) значение x,
-наибольшее
и наименьшее значение x.
Нормировка является адекватной, если
сложение всех показателей объекта для
сравнения с другими объектами имеет
смысл. Выполнив операцию нормировки,
мы можем перейти к измерению расстояний
между объектами.
Приведем несколько формул для измерения расстояния.
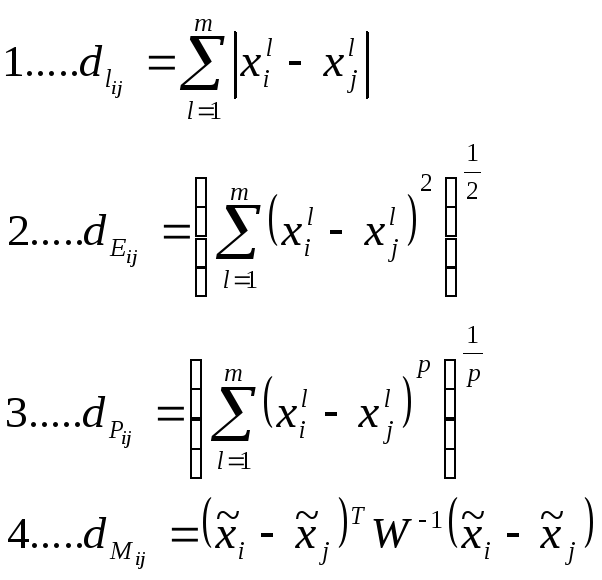
Линейное расстояние – с помощью линейного расстояния лучше всего обрабатываются «плоские» множества, расположенные почти на гиперплоскостях, особенно если они ортогональны каким либо координатным осям.
Евклидово расстояние – является самой популярной метрикой в кластерном анализе: оно отвечает интуитивным представлениям о близости и, кроме того, очень удачно вписывается своей квадратичной формой в традиционно статистические конструкции. Геометрически оно лучше всего объединяет объекты в шарообразных скоплениях.
Обобщенное степенное расстояние – представляет только математический интерес как универсальная метрика.
Расстояние Махаланобиса – особенная метрика, результаты ее применения могут существенно отличаться от других, в силу свойства усиления рассогласования коррелированных признаков. Также расстояние в данной метрике зависит от расстояний между другими точками.
Отметим что результаты работы алгоритмов классификации могут непредсказуемо меняться в зависимости от выбора способа измерения показателей.
Матрицу расстояний можно записать в следующем виде:
D
=
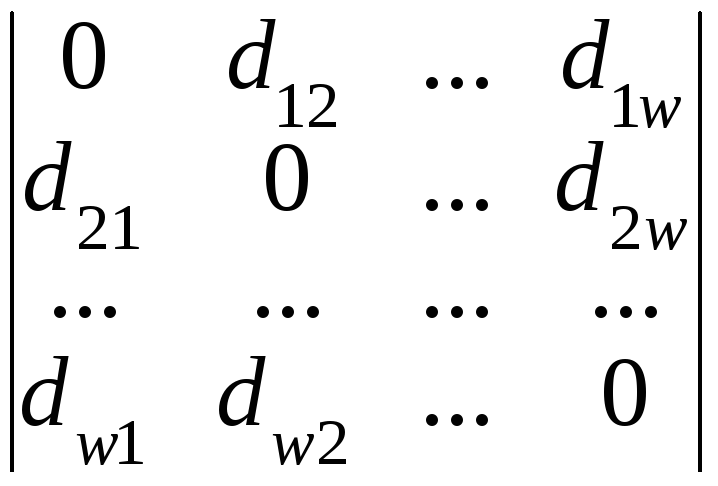
Здесь
символ
обозначает расстояние между элементамиi
и j.
Дальнейшее преобразование вышеприведенной матрицы заключается в том, что исчисленные расстояния разбиваются на классы по заранее установленным интервалам. Затем каждому выделенному классу присваивают условный знак: если элемент принадлежит интервалу, то пишут «X», иначе «-». Преобразованная таким образом таблица называется неупорядоченной диаграммой Чекановского (табл. 3.1).
Таблица 3.1.
Неупорядоченная диаграмма Чекановского
|
номера единиц |
1 |
2 |
… |
|
|
1 |
X |
- |
X |
- |
|
2 |
- |
- |
- |
X |
|
… |
… |
… |
… |
… |
|
w |
- |
X |
- |
X |
В приведенной неупорядоченной диаграмме очередность записи случайна. На это указывает явственный разброс символов, обозначающих разницу между изучаемыми элементами: наименьшее численное расстояние – «»; наибольшее расстояние, т.е. пары элементов, наиболее разнящиеся между собой, - «-». Для их линейного упорядочения следует произвести перегруппировку знаков таким образом, чтобы знаки «X» оказались как можно ближе к главной диагонали диаграммы. С этой целью строки и столбцы таблицы переставляются до тех пор, пока не получится упорядоченная диаграмма, из которой и получают сегменты рынка.