2.3 Генерация частичных произведений

В предыдущей части кратко описаны различные существующие архитектуры умножителей. Все они, вкратце, сводятся к двум шагам – сформировать группу частичных произведений, а затем сложить их для получения конечного результата. Были упомянуты различные способы сложения частичных произведений, но практически ничего не было сказано о способах их генерации. В этой главе описывается ряд способов, используемых для получения частичных произведений. Самый простой генератор частичных произведений имеет на выходе Nоперандов, гдеN– битовая длина множителя. Схема, предложенная Бутом, сокращает число частичных произведений примерно в два раза. Т.к. скорость работы и схемотехническая сложность зависят от числа частичных произведений, это усовершенствование может увеличить производительность и сократить схемотехнические затраты. Дальнейшие усовершенствования алгоритма Бута могут еще больше сократить число частичных произведений, но при этом время генерации любого частичного произведения не может быть меньше, чем время, требуемое для линейного сложенияN-битных операндов.

2.3.1 Классическая генерация частичных произведений

На рисунке 2.4 представлен процесс вычисления частичных произведений в простейшем случае (сложение столбиком). Разрядность элементов – 16.

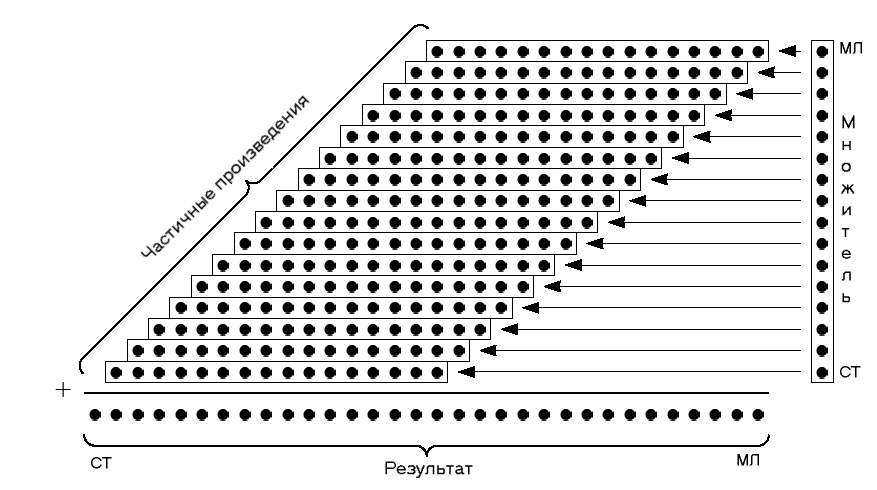
Рис 2.4

Каждая точка на рисунке – это один бит, принимающий значения {0,1}. Частичные произведения представлены горизонтальными строками точек. Они сдвинуты друг относительно друга для того, чтобы соответствовать различным арифметическим весам множителя.

Грубо говоря, общее число бит (256 для этого случая) в области частичных произведений пропорционально величине требуемого для реализации алгоритма оборудования. Кроме того, время работы такой схемы зависит от «высоты» секции частичных произведений (т.е. от максимального числа бит в каждой вертикальной колонке). Эта зависимость может менять свой характер от логарифмической (при реализации сложения в виде дерева) до линейной (когда суммирование реализовано строго последовательно). И все же, независимо от способа реализации, чем меньше частичных произведений, тем лучше.

Для данного случая, логика выбора частичных произведений очень проста. Она состоит из одного логического вентиля «И» на бит (см. рисунок 2.5).

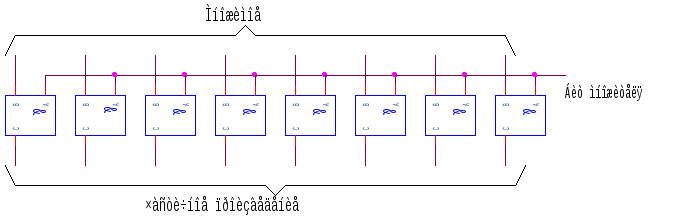
Рис 2.5 Схема выбора частичных произведений

2.3.2 Алгоритм Бута

Простейший алгоритм уменьшения числа частичных произведений, предложенный Бутом, состоит в следующем: биты множителя группируются по два и, в зависимости от значения битов в группе, из множества {0, M, 2M, 3M} выбирается один из четырех вариантов частичного произведения (M- множимое). Это сокращает число частичных произведений вдвое, но для 3Mтребует распространения переносов, перед тем, как будут сгенерированы следующие частичные произведения. Вместо этого используется модифицированный алгоритм Бута, который сокращает число частичных произведений меньше, чем в два раза, но не требует предварительного сложения для вычисления частичных произведений. Общая идея состоит в том, чтобы при декодировании множителя чуть усложнить работу, выбирая варианты частичных произведений из множества {0,M, 2M, 4M+ -M}. Все составляющие множества могут быть получены простыми логическими сдвигами и дополнением. Как можно видеть, элемент 3Mбыл заменен на 4M+ -M. В зависимости от значений битов смежной группы, или 4Mсдвигается в более значащую группу (становясь при этомM) или –Mсдвигается в менее значащую группу (становясь при этом –4M). РисунокX.Xдемонстрирует точечную диаграмму умножения двух 16тиразрядных чисел, используя модифицированный алгоритм Бута.

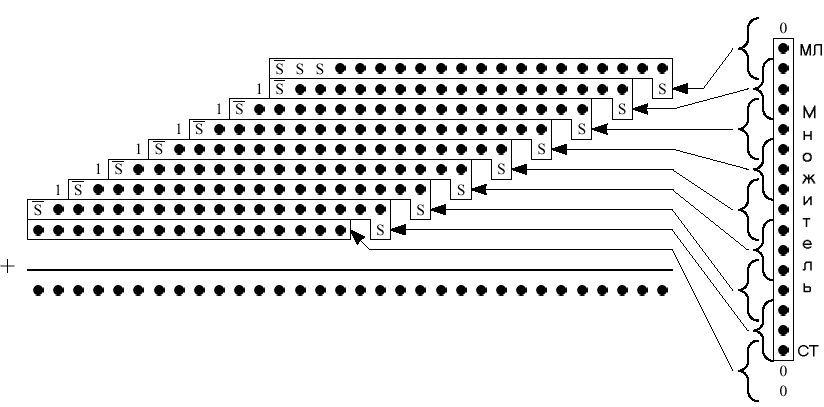
Таблица выбора частичных произведений
Биты множителя	Слагаемое
000	0
001	+Множимое
010	+Множимое
011	+2 xМножимое
100	-2 xМножимое
101	-Множимое
110	-Множимое
111	0

S= 0, если слагаемое положительно (4 верхние строки таблицы)

S= 1, если слагаемое отрицательно (4 нижние строки таблицы)

Рис 2.6

Множитель делится на пересекающиеся группы по 3 бита и каждая группа декодируется для выбора частичного произведения из таблицы. Каждое частичное произведение сдвинуто по отношению к соседям на 2 позиции. Число частичных произведений сократилось с 16 до 9.

В общем случае, число слагаемых будет [(n+2) / 2], гдеn– разрядность операнда. Различные слагаемые получаются простым сдвигом множимого. Отрицательные частичные произведения – побитовым дополнением к соответствующему положительному слагаемому и добавлением единицы к результату (битSна правой стороне рисунка). Число битов сократилось с 256 до 177. Это не чистый выигрыш, т.к. при этом дополнительно усложняется логика выборки частичных произведений.

Рассмотрим теперь метод сокращения затрат на распространение знаков частичных произведений. В общем случае появляется необходимость распространять знаки слагаемых в пределах разрядной сетки. Это увеличивает число бит, необходимых для сложения, так что избавимся от этого, используя алгоритм генерации переносов.

Пусть S₀–S₇– знаковые биты полученных нами частичных произведений (знак последнего слагаемогоS₉не играет никакой роли, поскольку оно всегда положительно или 0). Тогда сумма всех знаков может быть записана как

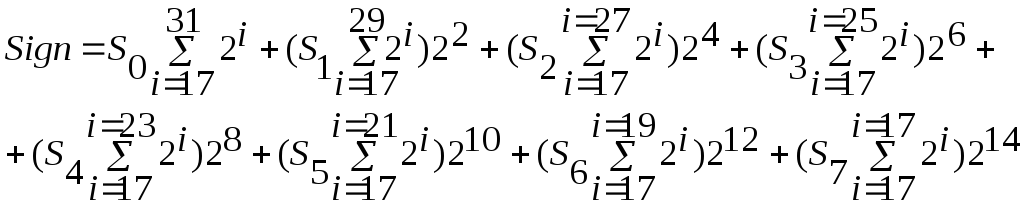(1)

Используя равенства и

Выражение (1) после простейших алгебраических преобразований и отбрасывания незначащей части, выходящей за пределы разрядной сетки, можно переписать так:

На этом месте можно остановится, и записать алгоритм генерации знака следующим образом:

• Инвертировать знак каждого значащего произведения и добавить его семнадцатой колонкой каждому частичному произведению.

• Добавить «1» восемнадцатым разрядом каждому частичному произведению.

• Добавить 1 в битовую колонку 17.

Несмотря на значительное уменьшение общего числа бит, число сумматоров уменьшится ненамного. Это происходит из-за увеличившегося числа бит в семнадцатой колонке (10 вместо 9). Для того, чтобы получить наиболее экономичное решение, используем модифицированный алгоритм генерации знака. Преобразуем выражение:

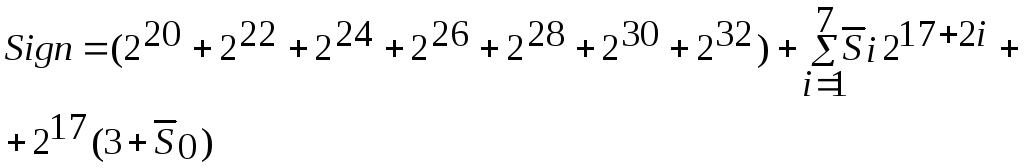
Последний член этого выражения принимает значения из множества {3,4} в зависимости от значения . Т.е. при, он равен «100» или «», а при, значение его равно «».

Распространение переноса сведено к добавлению единиц и знаков частичных произведений. На рисунке 2.7 – пример работающей схемы Бута:

Множитель = 63669₁₀= 1111100010110101

Множимое (М) = 40119₁₀= 1001110010110111

Рис 2.7