1.2 Введение

Одним из наиболее эффективных направлений анализа набора данных является анализ спектра полученных данных. Под данными в этом случае понимается произвольный набор значений-отсчетов, часто – полученный опытным путем. В качестве инструмента выступают различные дискретные преобразования, как то: «дискретное преобразование Фурье» (ДПФ), вейвлет-преобразованиe, и т.д. Полученные в результате преобразования значения - коэффициенты при базисных функциях (в случае ДПФ этоcosиsin) – составляют спектр исходного набора данных.

Вейвлет-преобразование характерно тем, что его базисные функции позиционированы не только во времени, но и в пространстве, что, является дополнительным преимуществом, по сравнению с ДПФ. Вместе с тем, ДПФ идеально подходит там, где сама природа исходных данных подвигает к тому, чтобы использовать в качестве базиса тригонометрические функции (анализ звуковых колебаний, и т.д.).

С точки зрения схемотехники, вычисление ДПФ – довольно трудоемкая задача. Согласно формуле вычисления ДПФ, , (N– количество исходных отсчетов,x(n) –n-ый отсчет,X(k) –k-ый коэффициент спектра), на вычисление одного коэффициента спектра идетNопераций умножения. Нетрудно представить, что для вычисления полного ДПФ нужно затратитьN²операций умножения, и столько же операций сложения. Быстрое преобразование Фурье позволяет сократить число операций умножения сN²доNlog₂(N). Для сравнения: при вычислении 4096-точечного ДПФ, разница в скорости между двумя алгоритмами составляет два порядка (!). БПФ в этом случае оказывается быстрее классического ДПФ где-то в 300 раз.

В данном дипломном проекте рассматривается аппаратная реализация быстрого преобразования Фурье, разработанная в виде специализированного микропроцессора. Особенностями реализации являются:

• небольшой размер ОЗУ на кристалле

• высокое быстродействие, обусловленное применяемым алгоритмом умножения и совмещением внутренних микроопераций МП при работе с внешним ОЗУ.

1.3 Бпф и его реализация

Какое количество вычислений требуется, чтобы вычислить дискретное преобразование Фурье Nточек? Долгое время, до середины 60-х, стандартным ответом было следующее.

Определим как, тогда формула ДПФ может быть записана: , гдеk= 0,…,N-1;x(n) – последовательность изNвременных отсчетов. Иными словами матрица, сW^nkв качестве (n,k)-ых элементов, умножается на векторx(n). В результате получается векторX(k). Очевидно, что операция матричного умножения требует для своей реализации О(N²) умножений иO(N²) сложений. Плюс небольшое число операций, необходимых для генерации степенейW(которые, впрочем, могут быть сгенерированы заранее).

Рассмотрим алгоритм быстрого преобразования Фурье с прореживанием по времени. Пусть длина исходной последовательности является степенью двойки, т.е.: N=2^L, гдеL> 0 – целое. Выделим из нее последовательность ее четных членов и последовательность нечетных, и сгруппируем соответствующим образом:

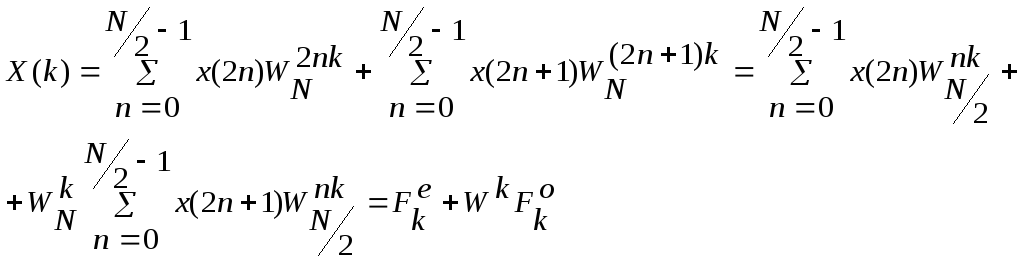
Каждая из сумм F_nпредставляет собойN/2-точечное ДПФ, которое аналогичным образом можно представить черезN/4-точечные, а те, в свою очередь, черезN/8-точечные и так далее, пока не останутся только одноточечные преобразования. Т.е. на каком-то шаге мы получим, чтоF^{eoeeoeooee…oee}=x(n) для некоторогоn. Сразу появляется вопрос – а каким наборам «е» и «о» соответствуют какие «n»? Ответ таков: инвертируйте порядок следования «е» и «о», затем положитеe= 0, аo= 1, и вы получите двоичное значениеn. Пример соответствия индексов дляN=8 можно видеть на рисунке 1.1.

Рис 1.1

Алгоритм вычисления БПФ, в результате, выглядит следующим образом: предположим, у нас есть вектор данных x(n). Расположим его значения в порядке двоичной инверсии номеров. Мы получили конечные, одноточечные преобразования. Затем происходит рекомбинация пар для вычисления частичных преобразований по следующим формулам:

X_m(p) =X_m+1(p)+W^dX_m+1(q)

X_m(q) =X_m+1(p)-W^dX_m+1(q), т.н. «бабочка», гдеmиm+1 – последовательные уровни преобразования, аW^d– соответствующие уровню коэффициенты.

Затем рекомбинируют смежные пары пар и т.д. до получения полного преобразования. На каждом уровне совершается порядка Nопераций умножения. Всего уровнейlog₂N. Следовательно весь алгоритм займет порядкаNlog₂Nопераций.

«Бабочка» - основной элемент преобразования. БПФ любой последовательности можно выразить через элементы-бабочки. Графически в дальнейшем будем обозначать ее так: (Рис 1.2)

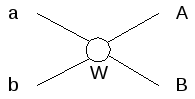
Рис. 1.2 Графическое обозначение «бабочки».

Архитектурно «бабочка» выглядит следующим образом:

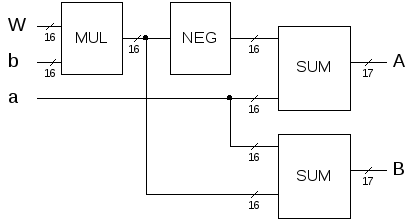
Как нетрудно заметить, основная задержка приходится на умножитель (остальные операции, как то получение отрицательного результата и суммирование, могут быть выполнены очень быстро). Проблема создания быстродействующего сумматора подробно рассмотрена во второй части данного дипломного проекта.

В нашем случае исходные операнды 16-тиразрядные. На выходе умножителя также 16-тиразрядное число (|W|1, младшие 16 разрядов отбрасываются, что в данном случае эквивалентно округлению). На выходе одного из конечных сумматоров теоретически может возникнуть переполнение. Для борьбы с этим используется адаптивный алгоритм, подробно описанный в следующем разделе.