2°. Фундаментальная система решений (фср).

Опред.: Фундаментальной системой решений ФСР называется любой базис пространства решений.

Теорема (о структуре общего решения О ЛОС.):

Если вектор-функции образуют ФСР, тоявляется решением ЛОС тогда и только тогда, когда..

- ФСР.

Билет №10

Фундаментальная матрица однородной системы и её свойства. Определитель Вронского.

(фундаментальная матрица).

Свойства фундаментальной матрицы:

1. - невырожденная.

2.

3. Вектор-функция тогда и только тогда является решением однородной системы, когда выполняется равенство:, где- постоянный вектор.

.

4. Теорема: Если - фундаментальная матрица, то матрица будет фундаментальной тогда и только тогда, когда, где- невырожденная постоянная матрица.

Доказательство:

.

- решение. - решение ЛОС.

. ,.

3°. Определитель Вронского (Вронскиниан).

Опред.: Определителем Вронского вектор-функций называется определитель

Решения (ЛОС) образуют ФСР тогда и только тогда, когда(хотя бы в одной точке).

- ФСР ,.

Билет № 11

5°. Линейные однородные дифференциальные уравнения -го порядка.

- ЛДУ

- линейный дифференциальный оператор -го порядка.

Если , то получаем линейное однородное дифференциальное уравнение (ЛОДУ)

Если , то получаем линейное неоднородное дифференциальное уравнение

Сумма решений ОДУ , а также произведение решения на число снова является решением.

Уравнению можно поставить в соответствие линейную однородную систему:

Каждому решению уравненияможно однозначно сопоставить решение

ЛОС (1)

Соответствие (1) не нарушается при сложении решений и умножении решения на число. Оно также сохраняет линейную зависимость или независимость решений.

на

Свойства уравнения :

1. Если - решение уравнениянаи,, тона.

2. Множество всех решений уравнения является линейным пространством размерности.

3. Решения уравнениялинейно независимы тогда и только тогда, когда они линейно независимы хотя бы при одном значении.

ФСР называется любой базис пространства решений, то есть любые линейно независимых решений.

4. Теорема о структуре общего решения:

Если функции образуют ФСР, то функцияявляется решением тогда и только тогда, когда, где.

- фундаментальная матрица.

Опред.: Определителем Вронского функций называется определитель

5. Решения уравненияобразуют ФСР тогда и только тогда, когда

.

Замечание: для линейной независимости произвольных функций условиеявляется достаточным, но не необходимым.

Пример:

на

ЛНУ, так как если

Билет №12

4°. Формула Лиувилля-Остроградского (Формула Якоби).

Вывод формулы:

- фундаментальная матрица

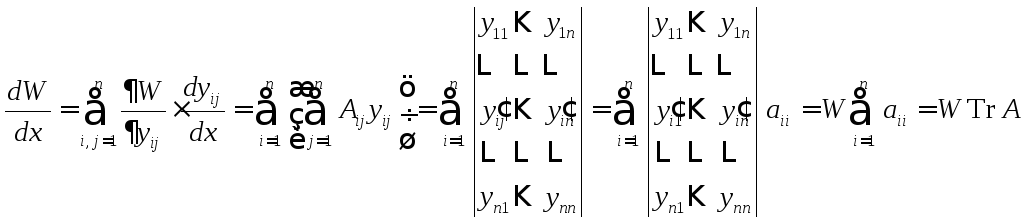
6°. Формула Лиувилля-Остроградского для ЛО ДУ-го порядка.

Билет № 13, 14

6°. Линейные неоднородные ДУ и системы.

Теорема (общее решение ЛНС):

, где - частное решение,- ФСР, соответствующая однородной системе,,.

Доказательство.:

. .

. Пусть - решения.

.

.

Для ЛНУ го порядка имеет место аналогичная теорема.

Билет № 15

7°. Метод вариации постоянных.

Данный метод позволяет найти частное решение.

находим находим.

Находим

Билет № 16

3°. ЛОУ -го порядка с постоянными коэффициентами.

, .

,

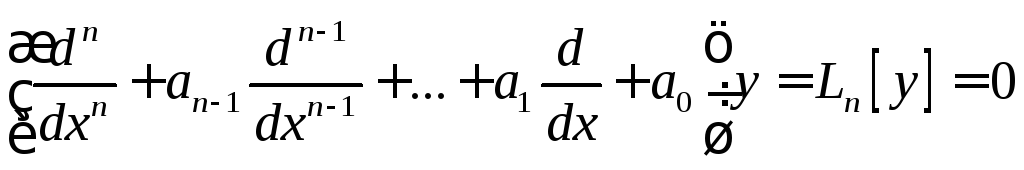
(характеристический многочлен).

Пусть- все корни характеристического многочлена.

1-й случай (различны):

Тогда - ФСР.

, .

Пусть

Если - действительны и являются ФСР.

Если ,

- корень ,

Следовательно - решения.

,

- линейно независимы

над линейно независимы над.

Билет № 17

3°. ЛОУ -го порядка с постоянными коэффициентами.

, .

,

(характеристический многочлен).

Пусть- все корни характеристического многочлена.

2-й случай (среди есть одинаковые):

Лемма 1:

Если - коренькратности характеристического многочлена , то

, линейно независимы над .

Доказательство:

{

}

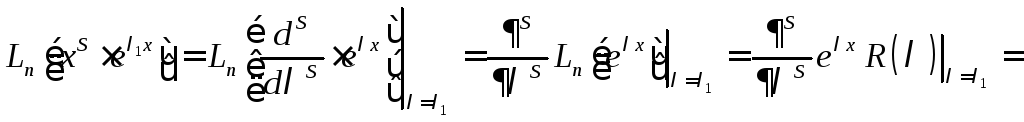
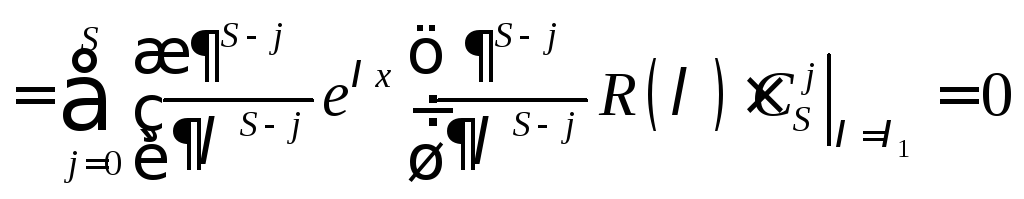
Лемма доказана.

- различные среди корней характеристического многочлена с кратностями ,

Лемма 2:

Если , где- многочлены с комплексными коэффициентами.

.

Доказательство (проводим индукцией по ):

База

Шаг - л. справа.

Продифференцируем это равенство раз:

Теорема:

- ФСР .

Доказательство:

Пусть ,

,

Линейно независимо над линейно независимо над.

Билет № 18