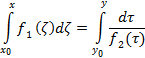- •Билет № 1
- •1°. Пример
- •2°. Определения.
- •3°. Геометрический смысл ду.
- •4°. Задача Коши.
- •1°. Уравнение в полных дифференциалах.
- •2°. Уравнения с разделяющимися переменными.
- •§ 4. Уравнения 1-го порядка, неразрешенные относительно производной.
- •3°. Связь нормальных систем с общими дифференциальными уравнениями (оду) n-го порядка.
- •5°. Нормальная линейная система (нлс).
- •1°. Линейная однородная система (лос).
- •2°. Фундаментальная система решений (фср).
- •Свойства уравнения :
- •4°. Формула Лиувилля-Остроградского (Формула Якоби).
- •4°. Линейные неоднородные уравнения - го порядка с постоянными коэффициентами и правой частью.
- •5°. Лос с постоянными коэффициентами.
- •5°. Лос с постоянными коэффициентами.
- •1°. Теорема о непрерывной зависимости решений от реальных условий.
- •Билет № 24
Билет № 1
1°. Пример
![]()
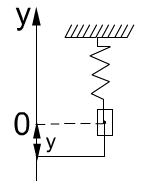 ,
,
![]() (
(![]() -
ускорение)
-
ускорение)
![]() (если подобрать
(если подобрать
![]() )
)
![]() ,
,
![]()
![]() (множество решений)
(множество решений)
![]() (положение груза
при
(положение груза
при
![]() )
)
![]() (положение груза
в начале колебаний)
(положение груза
в начале колебаний)
2°. Определения.
Опред.:
Обыкновенным
дифференциальным уравнением
![]() -ного
порядка называется уравнение
-ного
порядка называется уравнение![]() ,
где
,
где![]() -
независимая переменная,
-
независимая переменная,![]() -
искомая функция от
-
искомая функция от![]() ,
,![]() -
заданная функция от
-
заданная функция от![]() переменных.
переменных.
Опред.:
Функция
![]() называется решением дифференциального
уравнения на интервале
называется решением дифференциального
уравнения на интервале![]() ,
если при подстановке в это уравнение
она обращает его в тождество по
,
если при подстановке в это уравнение
она обращает его в тождество по![]() ,
на интервале
,
на интервале![]() .
.
![]() ,
,
![]() -
дифференциальное уравнение 1-го порядка.
-
дифференциальное уравнение 1-го порядка.
![]() -
решение ДУ
-
решение ДУ
![]() интеграл
ДУ
интеграл
ДУ
Опред.: Интегральная кривая ДУ - график любого решения ДУ.
Опред.: Интегрирование в квадратурах - выражение решения дифференциального уравнения с помощью элементарных функций и интегралов от них.
![]()
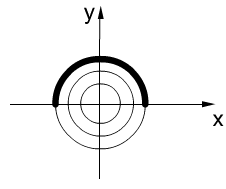 ,
,
![]()
![]() (неявная функция,
решение ДУ)
(неявная функция,
решение ДУ)
Опред.: Интегральная кривая – полуокр. (верхняя или нижняя)
![]()
![]()
![]()
![]() (общий интеграл
ДУ)
(общий интеграл
ДУ)
3°. Геометрический смысл ду.
![]() (это ДУ, разрешенное
относительно производной)
(это ДУ, разрешенное
относительно производной)
![]() -
определена в области
-
определена в области
![]() .
.
В каждой точке области мы знаем касательную к решению.
Опред.: Совокупность линий называют полем направлений, соответствующим дифференциальному уравнению.
С геометрической точки зрения нахождение решений ДУ- есть нахождение всех кривых, касательные в каждой точке к которым совпадают с соответствующими прямыми поля направлений.
4°. Задача Коши.
Опред.:
Задачей
Коши для уравнения
![]() наз. задача нахождения решения
наз. задача нахождения решения![]() этого
уравнения, удовлетворяющего условию:
этого
уравнения, удовлетворяющего условию:![]() ,
,![]() (н. у.).
(н. у.).
Билет № 2
1°. Уравнение в полных дифференциалах.
![]()
Опред.:
Уравнением
в полных дифференциалах называется
уравнение вида
![]() ,
левая часть которого - полный дифференциал
от некоторой функции
,
левая часть которого - полный дифференциал
от некоторой функции![]()

Теорема:
Всякое решение уравнения в полных
дифференциалах удовлетворяет уравнению
![]() для некоторого
для некоторого![]() .
.
Доказательство:
Пусть
![]() -
решение,
-
решение,![]() -
решение
-
решение![]()
![]()
![]() .
Теорема доказана.
.
Теорема доказана.
Теорема:
Пусть функции
![]() непрерывны в
непрерывны в![]() .
Тогда для того, чтобы уравнение
.
Тогда для того, чтобы уравнение![]() было уравнением в полных дифференциалах,
необходимо и достаточно условие
было уравнением в полных дифференциалах,
необходимо и достаточно условие![]() .
.
Доказательство:
Необходимость.
![]()
Достаточность.
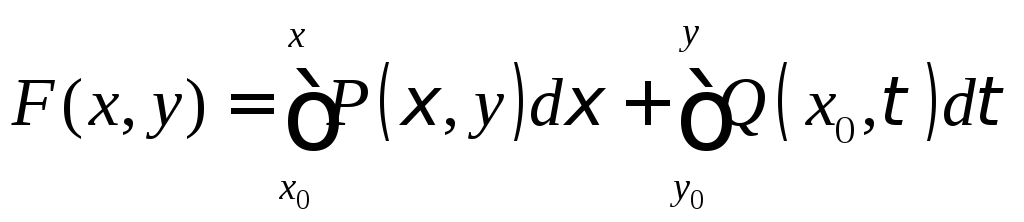
![]()

![]()
![]() ,
,
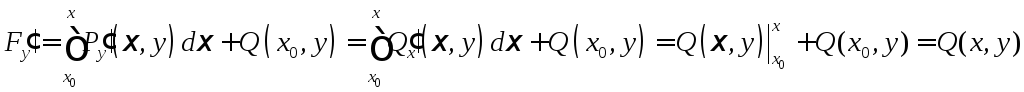
2°. Уравнения с разделяющимися переменными.
Опред.:
Уравнение
вида
![]()
![]()
![]() ,
где
,
где
![]() -
непрерывна на
-
непрерывна на![]() ,
,![]() непрерывна
на
непрерывна
на![]() ,
называется уравнением с разделяющимися
переменными.
,
называется уравнением с разделяющимися
переменными.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
|
6°. Интегрирующий множитель.
![]() ,
,
![]() ,
,
![]()
Если
![]() является
уравнением в полных дифференциалах, то
является
уравнением в полных дифференциалах, то
![]() называется
интегрирующим множителем.
называется
интегрирующим множителем.
Пример:
![]() ,
,![]() ,
,![]()
Билет № 3
3°. Линейные дифференциальные уравнения 1-го порядка.
![]()
Опред.:
Если функция
![]() ,
то уравнение называется линейным
однородным.
,
то уравнение называется линейным
однородным.
![]()
![]()
![]()
![]()
Лемма:
![]()
Доказательство:
![]() .
.
![]() .
.
![]() .
.
![]() -два частных
решения.
-два частных
решения.
![]()
![]()
Метод вариации постоянных.
![]()
![]()
![]()
![]()
![]()
4°. Уравнение Бернулли.
![]() ,
где
,
где
![]()
![]()
![]()
![]() ,
,
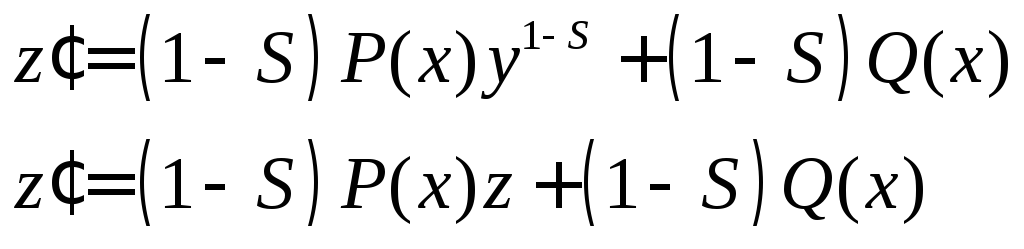
Если
![]() ,
то нужно смотреть, не потеряно ли решение
,
то нужно смотреть, не потеряно ли решение![]() .
.
5°. «Однородные» уравнения.
Опред.:
Дифференциальное
уравнение 1-го порядка называется
однородным, если его можно привести к
виду:
![]()
![]() =>
=>
![]() =>
=>![]() =>
=>![]()
Билет № 4
1°. Метрическое пространство.
Опред.:
Метрическое
пространство -
это множество
![]() ,
любой паре элементов
,
любой паре элементов![]() которого поставлено в соответствие
неотрицательное число
которого поставлено в соответствие
неотрицательное число![]() ,
называемое расстоянием между ними и
удовлетворяющее следующим аксиомам:
,
называемое расстоянием между ними и
удовлетворяющее следующим аксиомам:
1.
![]()
2.
![]()
3.
![]()
![]()
Пример:
![]()
![]()
![]()
Опред.:
![]() называется пределом последовательности
называется пределом последовательности![]() ,
если
,
если![]() при
при![]()
Опред.:
Последовательность
![]() называется
фундаментальной, если
называется
фундаментальной, если
![]()
![]()
![]()


Опред.: Метрическое пространство называется полным, если в нём всякая фундаментальная последовательность сходится к элементу этого же пространства.
Пример:
![]()
Теорема:
![]() -
полное метрическое пространство
-
полное метрическое пространство
Доказательство:
![]() -
фундаментальная последовательность
-
фундаментальная последовательность
![]()
![]()
Фиксируем
![]()
![]()
![]() -
числовая, причём справедливо неравенство
-
числовая, причём справедливо неравенство![]() -
фундаментальная
-
фундаментальная![]()
![]()
![]()
![]() ,
,
![]() -
сходится равномерно на
-
сходится равномерно на
![]()
![]()
2°. Принцип сжатых отображений.
![]()
![]() ,
,
![]()
Опред.:
Оператор
![]() называется
сжимающим, если
называется
сжимающим, если![]()
![]()
![]()
![]() называется
неподвижной точкой оператора
называется
неподвижной точкой оператора
![]() ,
если
,
если![]() .
.
Теорема:
Сжимающий оператор, отображающий полное метрическое пространство в себя, имеет единственную неподвижную точку.
Доказательство:
Докажем единственность.
![]()
![]()
Докажем существование.
![]()
![]()
![]()
![]()
![]() фундаментальная
фундаментальная
![]()
![]()
![]()
Билет №5
3°. Теорема о существовании и единственности решения дифференциального уравнения 1-го порядка.
Теорема.
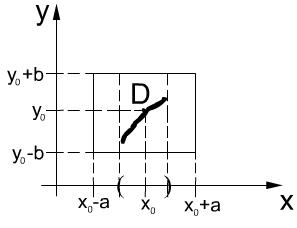 Пусть
функция
Пусть
функция
![]() непрерывна в прямоугольнике
непрерывна в прямоугольнике![]() ,
причем
,
причем![]() в
в![]() .
Тогда на интервале
.
Тогда на интервале![]() ,
где
,
где![]()
![]() ,
существует и единственно решение
дифференциального уравнения
,
существует и единственно решение
дифференциального уравнения![]() ,
удовлетворяющее условию
,
удовлетворяющее условию![]() .
.
Поставленная задача Коши эквивалентна решению интегрального уравнения.
Доказательство.
![]() на
на
![]() .
.
![]() .
.
![]()
![]() ,
,![]() на
на![]() ,
,![]()
![]()
![]() .
.
Проинтегрируем
это равенство на отрезке
![]() :
:![]() .
.
Рассмотрим
произвольный отрезок
![]() :
:![]()
Рассмотрим
метрическое пространство M,
состоящее из непрерывных функций на
отрезке
![]() и удовлетворяющих неравенству:
и удовлетворяющих неравенству:![]() на
на![]() ,M
,M![]()
![]()
![]()
![]() M.
M.
Рассмотрим
произвольную фундаментальную
последовательность
![]() -
худ. изM.
-
худ. изM.
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]() M
M
Рассмотрим на
пространстве M
сжимающий
оператор
![]() :
:![]() M
M![]() .
.
![]() ,
,
![]() M
M
![]()
![]()
![]()
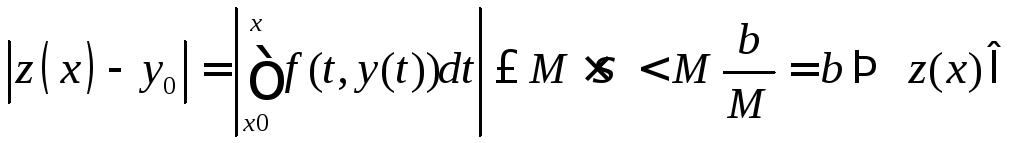 M.
M.
![]() ,
,
![]()
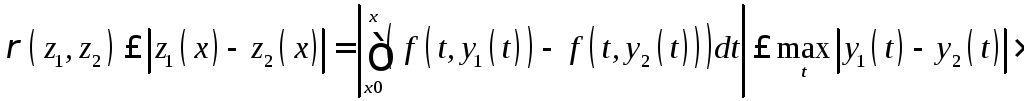
![]()
![]()
![]()
![]() M,
M,
![]()
Элемент
![]() является
функцией, удовлетворяющей интегральному
уравнению и следовательно исходной
задаче Коши.
является
функцией, удовлетворяющей интегральному
уравнению и следовательно исходной
задаче Коши.
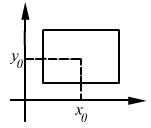
![]()
![]() -
непрерывна в
-
непрерывна в
![]()
![]()
![]()
Билет № 6