
Teoria_uprugosti_Ch2_Ledovskoy_12
.pdf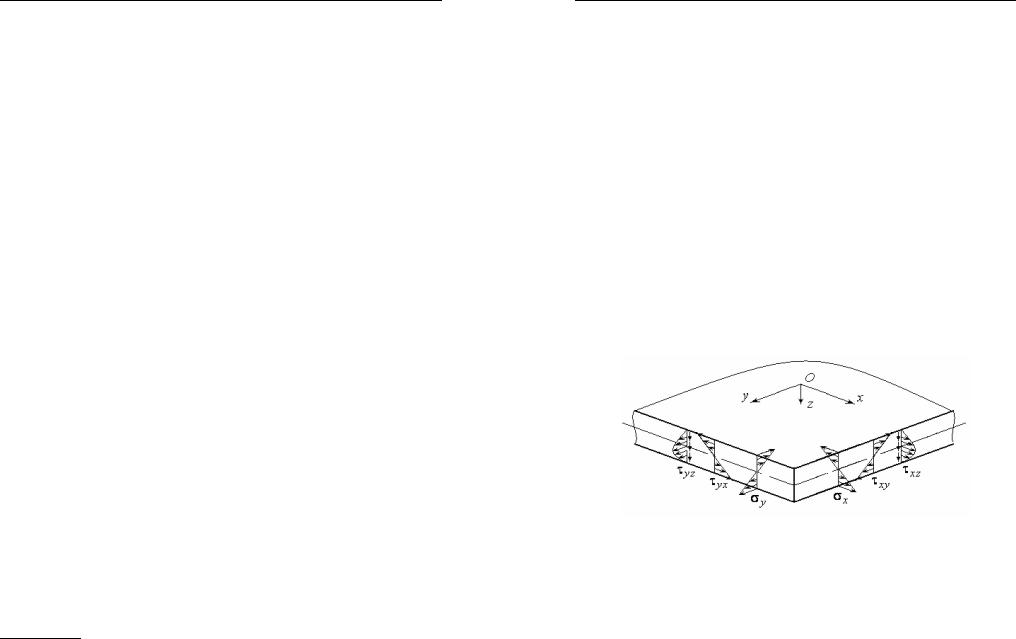
Теория упругости. Часть II
лась на расстоянии BA = z от последней. В результате деформации точки B и A,получивперемещение,займутположение B1 и A1 на этой
женормали,котораявсоответствииспервымдопущениемнеискривляется и остается нормальной к деформированной срединной повер-
хности. Проекция нормали на плоскость xOy после изгиба составит
с вертикалью угол, который равен углу между осью x и линией пересечения касательной плоскости к деформированной срединной по-
верхности в точке B1 с плоскости xOy.
Этот угол ввиду малости рассматриваемых деформаций может бытьпринятравнымсвоемутангенсу, который,всвоюочередь,равен частной производной прогиба точки B по координате x (см. рис. 31).
Вследствие поворота нормали точка A получит горизонтальное перемещение, проекция которого на ось x отрицательна, так как она направлена в сторону, противоположную положительному направлению оси x, и это перемещение равно
u = −z |
∂w |
, |
(5.6) |
|
∂x |
|
|
где w = w(x, y) – прогиб точки B(x, y), принадлежащей срединной
плоскости плиты, через которую проходит нормаль1.
Аналогично можно показать, что проекция перемещения
точки A на ось y будет равна |
|
|
∂w |
|
|
|
|
|
|
|
|
||||
|
|
|
|
v = −z |
. |
|
|
|
|
|
(5.7) |
||||
|
|
|
|
∂y |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пользуясь (5.6) и (5.7), найдем компоненты линейной и угловой |
|||||||||||||||
деформации εx ,εy |
и γxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εx = |
∂u |
= − |
∂2 w |
z; |
εy = |
|
∂v |
|
= − |
∂2 w |
z; |
||||
∂ x |
∂ x2 |
|
∂ y |
∂ y2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
γxy = |
∂u + |
∂v |
= −2 |
|
∂ |
2 |
w |
z. |
(5.8) |
|||||
|
|
|
|
|
|||||||||||
|
∂ x |
∂ x ∂ y |
|
||||||||||||
|
|
|
∂ y |
|
|
|
|
|
|||||||
1 В самом общем случае деформации плиты точка В также получит горизонтальное перемещение.Однакопридействиитольковертикальныхнагрузокэтиперемещениябудутвеличинамивысшего порядка малости по сравнению с определяемыми и не повлияют на напряженное состояние плиты.
Задача 5. Расчет тонких плит при поперечном изгибе
Компоненты напряжений (5.5) с учетом соотношений (5.8) получат следующие выражения через прогибы срединной плоскости:
σx = − |
|
|
E z |
|
|
∂2 w |
+µ |
∂2w |
; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
−µ2 |
∂ x2 |
∂ y2 |
|
||||||||||
|
|
|
|
|
|
|
||||||||
σy = − |
|
|
E z |
|
|
∂2 w |
+µ |
∂2w |
; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
(5.9) |
|||
1 |
−µ2 |
|
∂ y2 |
∂ x2 |
||||||||||
|
|
|
|
|
|
|||||||||
τxy = − |
|
E z |
|
|
∂2w |
. |
|
|
|
|||||
1+µ ∂ x ∂ y |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||
Извыражений(5.9)следует,чтонормальныенапряжения σx ,σy
и горизонтальные касательные напряжения изменяются по высоте сечения по линейному закону (рис. 32). Они принимают максимальныезначениявточках,прилегающихкповерхностямплиты,анасрединной плоскости равны нулю.
Рис. 32
Зная компоненты напряжений σx, σy, τxy , нетрудно определить
напряжения τxz и τyz .
Используя первое и второе уравнения равновесия (3.1) при отсутствии объемных сил, параллельных осям x и y, получим
60 |
61 |
Теория упругости. Часть II
|
|
|
|
|
|
|
|
E |
|
|
|
h2 |
− z2 |
|
∂ |
2w; |
||
|
|
|
|
|
τ |
xz |
= − |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
2(1−µ |
|
|
|
4 |
|
|
∂x |
|
|||
|
|
|
|
|
|
|
|
|
) |
|
|
(5.10) |
||||||
|
|
|
|
|
|
|
|
E |
|
|
|
h2 |
|
|
∂ |
|||
|
|
|
|
|
|
|
|
|
|
|
− z2 |
2w, |
||||||
|
|
|
|
|
τ |
yz |
= − |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2(1−µ |
|
|
|
4 |
|
|
∂ y |
|
|||
|
|
∂2 |
|
∂2 |
|
|
|
|
) |
|
|
|
||||||
где 2 |
= |
+ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∂x2 |
∂y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражения (5.10) удовлетворяют граничным условиям, согласно которым на поверхностях плиты нет касательной нагрузки, т. е.
при z = ± h2 должно быть τxz = τyz = 0.
Нарис.32всекомпонентынапряжений,действующиенижеплоскости xOy, имеют положительные значения (см., например, задачу 1).
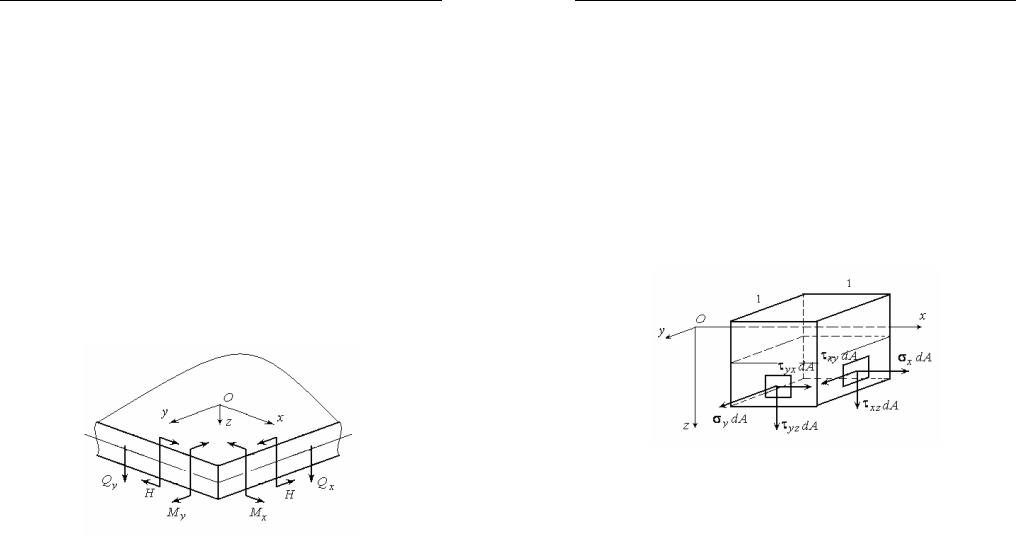
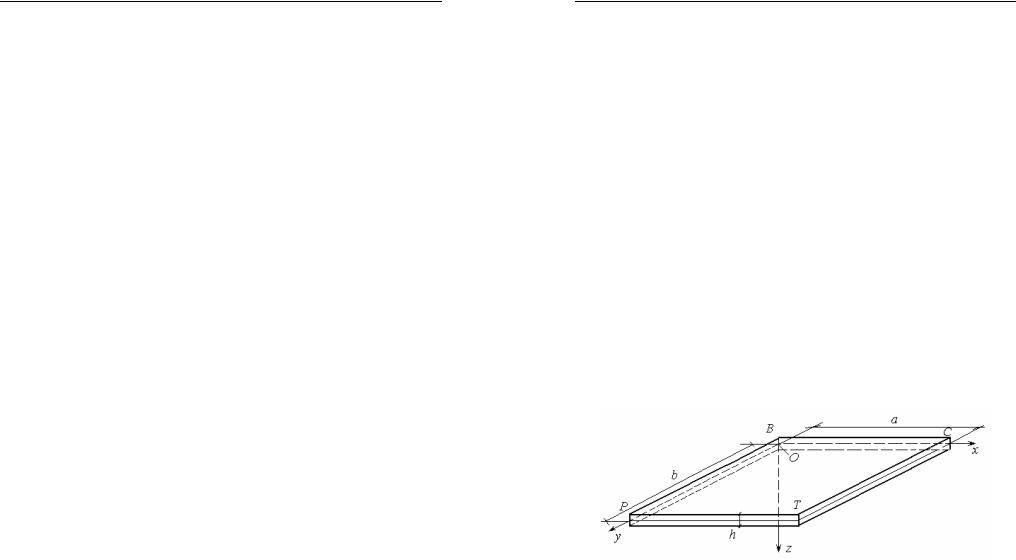
Очевидно, что равнодействующие элементарных усилий σx dA, σydA и τxy dA равны нулю. Эти усилия создают пары, показанные на рис. 33.
Рис. 33
Напряжения σx и σy создадут соответственно изгибающие усилия M x по сечению, перпендикулярному оси x, и M y , действующе-
му по сечению, перпендикулярному оси y .
Горизонтальные касательные напряжения τxy и τyx , действующие по перпендикулярным сечениям, создадут крутящие усилия.
Задача 5. Расчет тонких плит при поперечном изгибе
Вследствие закона парности касательных напряжений соответствующие усилия будут равны по величине друг другу (см. рис. 33).
Вертикальныекасательныенапряжения τxz и τyz изменяютсяпо высоте сечения по параболическому закону. Максимальные значения они принимают на нейтральной плоскости при z = 0 . Эти напряжения создают поперечные усилия Qx иQy (см. рис. 32, 33).
5.3. Выражения погонных усилий через прогибы срединной поверхности плиты
На рис. 34 показан выделенный из плиты параллелепипед сечениями,параллельнымикоординатнымплоскостям xOz и yOz .Шири-
ны этого параллелепипеда вдоль осей x и y равны единице, а высота равна толщине плиты h.
Рис. 34
Используявыражениедлянормальногонапряжения σx (5.9),при
dA =1 dz найдем,чтопогонныйизгибающиймомент M x долженбыть равен
+h |
|
|
|
E |
|
|
∂2w |
|
∂2w |
|
+h |
|
|
||||||||
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|||||||||||
M x = ∫σx z d z = − |
|
|
|
|
|
|
|
|
2 +µ |
|
|
|
|
∫ z |
dz = |
||||||
1−µ |
2 |
|
∂x |
∂y |
2 |
|
|||||||||||||||
− |
h |
|
|
|
|
|
|
|
|
− |
h |
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Eh3 |
|
|
|
∂ |
2w |
|
∂2w |
|
|
|
|
|
|
|||||
|
|
= − |
|
|
|
|
|
|
|
|
+µ |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|||||
|
|
|
12(1−µ |
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|||||||
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
||||||||
62 |
63 |

Теория упругости. Часть II
Введем обозначение
Eh3 |
= D |
(5.11) |
||
12(1 |
−µ2 ) |
|||
|
|
|||
ибудемназыватьэтувеличину цилиндрическойжесткостьюплиты.
Цилиндрическая жесткость D отличаетсяот балочной жесткости при изгибе балки прямоугольного сечения единичной ширины
свысотой h EI = Eh3 множителем (1 −µ2 ), расположеннымвзнаме-
12
нателе. Поэтому цилиндрическая жесткость всегда, но не на очень много, больше балочной.
Таким образом,
|
∂2w |
|
∂2w |
(5.12) |
|||
M x = −D |
∂x |
2 |
+µ |
∂ y |
2 |
. |
|
|
|
|
|
|
|
||
Аналогично получим
|
∂2w |
|
∂2w |
(5.13) |
|||
M y = −D |
∂ y |
2 |
+µ |
∂x |
2 |
. |
|
|
|
|
|
|
|
||
Пользуясь формулой для касательных напряжений τxy из (5.9), найдем выражение погонного крутящего усилия
+h |
|
|
E ∂2 w |
+h |
|
|
|
|
|
|
|
|
|
Eh3 |
|
|
|
∂2 w |
|
|||||||||
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
H = ∫τxy z d z = − |
|
|
|
|
|
|
|
|
∫ |
|
z |
|
d z = − |
|
|
|
|
|
|
|
. |
|||||||
1 +µ ∂ x ∂ y |
|
|
12(1 +µ) ∂ x ∂ y |
|||||||||||||||||||||||||
− |
h |
|
− |
h |
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда, учитывая (5.11), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
H = −D(1−µ) |
|
|
∂ |
2w |
. |
|
|
|
|
|
|
|
|
|
(5.14) |
||||||||||
|
|
|
∂x ∂ y |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Найдем погонные поперечные усилия Qx |
|
и Qy : |
|
|
|
|
|
|||||||||||||||||||||
|
+h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+h |
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
E |
|
|
|
∂w |
|
|
2 |
|
2 h2 |
|
2 |
|
|
||||||||
Qx = ∫τxy d z = − |
|
|
|
|
|
|
|
|
|
|
( w)∫ |
|
|
− z |
|
|
|
|||||||||||
2(1−µ |
2 |
) |
|
∂ x |
|
|
4 |
|
d z, |
|
||||||||||||||||||
|
− |
h |
|
|
|
|
|
|
|
|
− |
h |
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача 5. Расчет тонких плит при поперечном изгибе
откуда |
|
|
|
|
|
|
Qx = −D |
∂ |
|
( 2w) |
|
(5.15) |
|
∂x |
|
|||||
и аналогично |
|
|
|
|
||
|
|
|
|
|
||
Qy = −D |
∂ |
|
( 2w). |
|
(5.16) |
|
∂ y |
|
|
||||
|
|
|
|
|
||
5.4. Выражения напряжений через погонные усилия |
||||||
Сопоставив выражение для напряжения σx из (5.9) и (5.12), ис- |
||||||
ключив из этих выражений прогибы w и обозначив |
h3 |
= I, получим |
||||
12 |
||||||
|
|
|
|
|
||
формулу, связывающую напряжение σx с погонным изгибающим моментом M x :
σx = MI x z.
Аналогичные формулы получим, рассматривая совместно вы-
ражения (5.9), (5.13) и (5.14) и, наконец, (5.10), (5.15) и (5.16).
В результате найдем, что |
|
M y |
|
|
|
|
|
|
|
||||||
σx = |
M |
x z; |
|
σy = |
z; |
τxy |
= |
H |
z; |
||||||
I |
|
|
I |
I |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Q |
|
Sотс |
|
|
|
|
|
Qy Sотс |
(5.17) |
|||
|
|
|
x |
|
|
|
|
|
|
||||||
|
τxz |
= |
|
|
; |
|
τyz |
= |
|
|
|
. |
|
||
|
|
I |
|
I |
|
|
|
||||||||
|
|
|
|
|
|
|
Sотс |
|
|
|
|
|
|||
В последних двух формулах |
(4.66) – статический момент |
||||||||||||||
части сечения, отсекаемой уровнем,на котором определяются напряжения τxz и τyz относительно нейтральной линии.
5.5. Дифференциальное уравнение прогибов плиты. Граничные условия
Задача определения прогибов сводится к интегрированию дифференциального уравнения Софи Жермен
64 |
65 |
Теория упругости. Часть II
2 2w = |
∂4w |
+ 2 |
∂4w |
+ |
∂4w |
= q(x,y). |
(5.18) |
|
∂x4 |
∂x2 ∂ y2 |
∂ y4 |
||||||
|
|
|
D |
|
Найдя прогибы в виде определенной функции координат x и y , решаем фактически задачу определения напряженно-деформирован- ного состояния плиты, так как, зная функцию прогибов, при помощи приведенных выше формул простым дифференцированием можно определить напряжения или погонные усилия.
Интегралы уравнения (5.18) должны подчиняться граничным условиям задачи. Эти условия определяются способом закрепления контура плиты и характером действующих на плиту нагрузок.
Напряженно-деформированное состояние плиты в каждой точ-
ке K ее контура определяется, во-первых, двумя кинематическими факторами:
•прогибом w(K);
•углом наклона касательной плоскости в точке K к деформированной срединной поверхности.
Угол наклона определяется производной прогиба по координа-
те, измеряемой вдоль нормали n |
|
∂w |
к контуру – |
. |
|
|
|
|
|
|
∂n K |
Во-вторых, обозначенное состояние определяется силовыми факторами:изгибающими,крутящимиипоперечнымиусилиями,связанными с производными от прогибов ранее установленными соотношениями
|
∂2 w |
|
|
∂2 w |
|
|
||||
M n = −D |
|
|
2 |
+µ |
|
|
|
; |
(5.19а) |
|
∂n |
∂S |
2 |
||||||||
|
|
|
|
|
|
|
|
|||
H = −D(1−µ) |
∂2w |
; |
|
|
(5.19б) |
|||||
∂n |
∂S |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
Q = −D |
∂ |
( 2w). |
|
|
|
(5.19в) |
||||
|
|
|
|
|||||||
n |
|
∂n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
В рамках приближенной теории при любом опирании контура можно поставить только два из перечисленных граничных условий.
Задача 5. Расчет тонких плит при поперечном изгибе
Постановка трех условий (5.19а–5.19в) делает задачу неразрешимой. Опираясь на принцип Сен-Венана, граничные условия смягчают, заменяя два из трех заданных условийодним, вдостаточной мере эквивалентным им.
Для простоты ознакомления с граничными условиями, соответствующими различным способам опирания и нагружения плит, рассмотрим прямоугольную плиту, края которой перпендикулярны осям x и y (рис. 35). На каждом краю плиты должно быть задано по два граничных условия для функции w.
ЗАЩЕМЛЕННЫЙ КРАЙ Пусть край ВС (см. рис. 35) защемлен. Тогда граничные условия
на этом крае будут иметь следующий вид:
при y = 0 w = 0; при y = 0 |
∂w |
= 0. |
(5.20а) |
||
|
∂y |
|
|
|
|
Если защемлен край CT, параллельный оси y , то |
|
||||
при x = a w = 0; при x = a |
|
∂w |
= 0. |
(5.20б) |
|
|
∂x |
|
|||
Рис. 35
На защемленном краю крутящий момент H всегда равен нулю.
Например, на всем краю CT ∂∂wx = 0. Тогда и смешанная производная
66 |
67 |

|
|
|
|
|
|
Теория упругости. Часть II |
|
∂2w |
|
∂ |
|
∂w |
|
|
|
= |
|
|
|
равна нулю. Следовательно, и крутящее усилие H |
|
|
|
||||
|
∂x∂ y |
|
|
|
|
|
|
|
∂ y |
∂x |
|
||
(см. (5.14)) также равно нулю.
Реакция защемленного края представляется опорными реактивными парами и вертикальными усилиями, распределенными по длине края. Их интенсивность определяется при этом формулами (5.12)
и (5.15) или (5.13) и (5.16).
СВОБОДНОЕ ШАРНИРНОЕ ОПИРАНИЕ
Если,например, крайCT призначении x = a шарнирнооперт,то его прогибы равны нулю (рис. 36). Одновременно этот край может свободно поворачиваться относительно оси, параллельной оси y ,
и погонные изгибающие моменты M x обращаются в нуль. Граничные условия на этом крае будут иметь следующий вид:
|
|
|
|
|
|
∂2 w |
∂2 w |
|
||||
|
(w)x=a = 0; |
|
|
|
|
|
|
2 +µ |
|
|
|
(5.21) |
|
(M x )x=a = −D |
∂ x |
∂ y |
2 |
= 0. |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Второе условие из (5.21) можно уп- |
||||||||
|
|
|
|
ростить, учитывая, что на всем протяже- |
||||||||
|
|
|
|
нии CT (w)x=a = 0. Тогда вторая произ- |
||||||||
|
|
|
|
водная |
∂2w |
(пропорциональная кривиз- |
||||||
|
|
|
|
∂ y |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
не края CТ в плоскости yOz) тоже равна |
||||||||
|
Рис. 36 |
|
|
нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
Итак, граничные условия для шар- |
||||||||
нирно-опертого края CТ имеют следующий вид: |
|
|
|
|||||||||
• |
при x = a w = 0; |
|
|
|
|
|
|
|
|
(5.22) |
||
• |
при x = a |
∂2w |
= |
0. |
|
|
|
|
|
|
|
(5.23) |
∂ x2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Одновременно шарнирное опирание способно создавать только вертикальные реакции в прилегающих и параллельных краю сечени-
Задача 5. Расчет тонких плит при поперечном изгибе
ях. Оно не может создавать горизонтальные реактивные силы, которые подобны касательным усилиям, создающим крутящие пары H.
Это противоречие, связанное с приближенностью теориейизгиба плит, заставляет предполагать, что в рассматриваемых областях происходитпреобразованиекасательныхнапряженийввертикальные усилия.
Следовательно, в сечении плиты x = a, бесконечно близко прилегающему к шарнирной опоре, действующее усилие приводится к вертикально распределенным силам интенсивностью
Vx = Qx + ∂∂Hy
и сосредоточенным силам VC = HC и VT = −HT (см. рис. 36). Эти
усилия возникают в точках C и T , принадлежащих углам плиты. Им
должны соответствовать равные по величине и противоположно направленные реакции на шарнирной опоре.
Выявленное наличиевуглахплитсосредоточенныхреактивных сил(насамомделе,по-видимому,сил,распределенныхнанебольших участках, но большой интенсивности) подтверждается экспериментально.
Реактивную распределенную нагрузку, действующую на краю CТ, можно выразить через прогибы срединной поверхности плиты:
|
∂H |
|
|
∂ |
|
|
2 |
|
|
|
|
∂ |
|
∂2 w |
|
|
||
Vx = Qx + |
|
= −D |
|
|
( w)+ (1 −µ) |
|
|
|
|
|
= |
|||||||
∂ y |
∂ x |
∂ y |
|
∂ x ∂ y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= −D |
∂ |
|
∂2w |
|
∂2w |
|
|
|
|
|
|||||||
|
|
|
∂x |
2 |
+(2 −µ) |
∂ y |
2 |
. |
|
|
|
(5.24) |
||||||
|
|
|
|
|
||||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|||||
Еслибы шарнирное опирание былобы не накраю CT, а накраю TP, то для этого края было бы задано:
• |
при y = b w = 0; |
(5.25) |
|||
• |
при y = b |
∂2w |
= 0. |
(5.26) |
|
∂ y2 |
|||||
|
|
|
|
||
Величинараспределеннойпоэтомукраювертикальнойреактивной нагрузки может быть найдена после отыскания решения уравне-
68 |
69 |

Теория упругости. Часть II
ния (5.18), удовлетворяющего всем граничным условиям задачи. Для этого нужно продифференцировать прогибы по формуле, аналогичной формуле (5.24):
Vy = −D |
∂ |
|
∂2w |
|
|
∂2w |
|
|
|
|
∂ y2 |
+(2 |
−µ) |
∂x2 |
. |
(5.27) |
|
|
||||||||
|
∂ y |
|
|
|
||||
В углах С и T обязательно появятся сосредоточенные реактивные силы RC , RT :
R |
= H |
C |
= −D(1 |
−µ) |
|
∂2w |
|
при x = a; y = 0; |
|
|
|
||||||||
C |
|
|
|
|
|
∂x∂ y |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
= −H |
T |
= D(1 |
−µ) |
∂2w |
|
при x = a; y = b. |
||
|
|
||||||||
T |
|
|
|
|
|
∂x∂ y |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если прямоугольная плита шарнирно оперта по всем четырем граням, то в ее углах появятся реактивные опорные силы:
RC = 2HC ; |
RT = −2HR ; |
(5.28) |
|
RP = 2HP ; |
RB = −2HB. |
||
|
При обычной направленной вниз нагрузке реактивные силы, действующие в углах плит, будут направлены тоже вниз, т. е. они будут противодействовать подъему углов плиты вверх.
КРАЙ, СВОБОДНЫЙ ОТ ОПИРАНИЯ
Если край CT свободен от опирания и на него не приложены никакие нагрузки, то должны выполняться три условия:
M x = 0; Qx = 0; H = 0.
Не имея возможности в рамках приближенной теории удовлетворить одновременно всем этим условиям, их смягчают, подчиняя решение задачи только двум условиям:
M x = 0; Vx = Qx + ∂∂Hy = 0.
Последним условием заменяют более жесткое условие
Qx = 0; H = 0.
Задача 5. Расчет тонких плит при поперечном изгибе
Выражая граничные условия через прогибы срединной поверхности, найдем, что для края, свободного от опирания и параллельного оси y, должно быть:
|
|
∂2 w |
|
|
∂2 w |
|
|
|
|
|||
1. M x = −D |
|
|
|
+ µ |
|
|
= 0; |
|
|
|||
∂ x2 |
∂ y2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
(5.29) |
||||
2.Vx = −D |
∂ |
∂2 w |
|
|
|
|
∂2 w |
|||||
|
|
|
∂ x2 |
+ (2 −µ) |
∂ y2 |
|
= 0. |
|||||
|
|
|||||||||||
|
∂ x |
|
|
|
|
|
|
|||||
Для края, свободного от опирания и параллельного оси x , аналогично должно быть:
1. |
∂2w |
+µ |
∂2w |
= 0; |
|
|
|
|||
∂ y2 |
∂x2 |
|
|
|
||||||
|
|
|
|
|
(5.30) |
|||||
|
|
∂ |
|
∂2w |
|
|
∂2w |
|||
2. |
|
+ (2 −µ) |
= 0. |
|||||||
|
|
|
∂ y2 |
∂x2 |
|
|||||
|
|
|||||||||
|
|
∂ y |
|
|
|
|
||||
Если к краю, свободному от опирания, приложена распределеннаясвободнаянагрузка,товторыеизграничныхусловий(5.29)и(5.30) изменяются. Так, например, для края CT должны быть выполнены следующие условия:
1. |
∂2 w |
+µ |
∂2 w |
|
= 0; |
|
|
|
|
||
∂ x2 |
∂ y2 |
|
|
|
(5.31) |
||||||
|
|
|
|
|
|
|
|||||
|
|
∂ |
∂2 w |
|
|
∂2 w |
|||||
2. − D |
+ (2 |
−µ) |
= F(y). |
||||||||
|
|
∂ x2 |
∂ y2 |
|
|||||||
|
|||||||||||
|
|
∂ x |
|
|
|
|
|||||
УПРУГО ОПЕРТЫЙ ИЛИ УПРУГО ЗАЩЕМЛЕННЫЙ КРАЙ Если, например, край плиты при x = a жестко соединен с поддерживающейее балкой (см. рис. 35), то прогиб и угол поворота края относительно оси, параллельной оси y , не будут равны нулю и одно-
временно
70 |
71 |

Теория упругости. Часть II
Vx = −D |
|
∂3w |
+ |
(2 −µ) |
|
∂3w |
|
|
≠ 0; |
||||||
|
|
|
|
|
|
|
|
||||||||
∂ x3 |
∂ x ∂ y2 |
||||||||||||||
|
|
|
|
|
|
|
x=a |
||||||||
|
|
|
|
|
∂2w |
|
|
∂2w |
|
|
|
||||
M |
x |
= −D |
|
|
+µ |
|
|
|
|
|
≠ 0. |
||||
|
2 |
|
2 |
|
|
||||||||||
|
|
|
|
∂ x |
|
|
∂ y |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x=a |
|
||||
Формулирование граничных условий с учетом жесткостей поддерживающей балки при ее изгибе и кручении можно найти во многихмонографиях, например, вкнигеС. П.Тимошенко,С. Войновско- го-Кригера «Пластинки и оболочки» [3].
5.6.Пример расчета плиты при поперечном изгибе
5.6.1.Постановка задачи
Рассматривается прямоугольная плита постоянной толщины h , края которой параллельны осям x и y (см. рис. 35).
До нагружения координатная плоскость x y совпадает с ее срединной плоскостью, а ось z направлена вниз. Задачу о напряженнодеформированном состоянии плиты предлагается решить обратным методом,полагая,чтовыражениедляпрогибовточексрединнойплоскости по оси z имеет следующий вид:
w = A x2 (x − a) y2 , |
(5.32) |
где A –некотораяпостояннаявеличина,котораявданнойзадачепред- полагается известной.
Полагаем, что µ = 0,25 и b = a . Требуется определить:
•поверхностные нагрузки на плиту, вызывающие прогибы (5.32) точек срединной плоскости;
•граничные условия на контуре плиты, которым соответствуют прогибы (5.32);
•погонные усилия в окрестности заданной точки K с координатами из табл. 5.2 в первой части учебно-методического пособия.
Задача 5. Расчет тонких плит при поперечном изгибе
5.6.2.Решение задачи
1.Определение распределенной поверхностной нагрузки
Поверхностнаянагрузкавходитвдифференциальноеуравнение (5.18) прогибов срединной плоскости. Чтобы определить нагрузку из этого уравнения, найдем частные производные функции w:
|
|
∂w = A 2x(x −a)y2 + Ax2 y2 = Ay2 (3x2 −2ax); |
|
||||||||||||||||||||
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.32а) |
|
|
|
∂2 w |
|
2 |
|
|
|
∂3 w |
|
|
2 |
|
∂4 w |
|
|||||||||
|
|
= Ay |
(6x −2a); |
= Ay |
6; |
= 0; |
|
||||||||||||||||
|
|
∂x2 |
|
∂x3 |
|
|
∂x4 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∂w |
= Ax |
2 |
(x |
−a)2 y; |
∂w2 |
= Ax |
2 |
(x −a)2; |
∂w3 |
= |
∂w4 |
= 0; |
|||||||||||
∂ y |
|
∂ y2 |
|
|
∂ y |
3 |
∂ y4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.32б) |
|||||
|
|
∂w3 |
|
|
|
|
|
|
|
|
∂w4 |
|
|
|
|
|
|
|
|
||||
|
|
= A 2 y(6x −2a); |
|
|
|
|
|
|
= A 2(6x −2a). |
||||||||||||||
|
|
∂x2∂ y |
|
|
∂x2∂ y2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Подставляя найденные производные в уравнение (5.18), полу- |
|||||||||||||||||||||||
чим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 4A(3x − a) = |
q |
|
|
|
|
|
|
|
|||||||
или |
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q =8AD(3x − a). |
|
|
|
|
|
(5.33) |
|||||||||
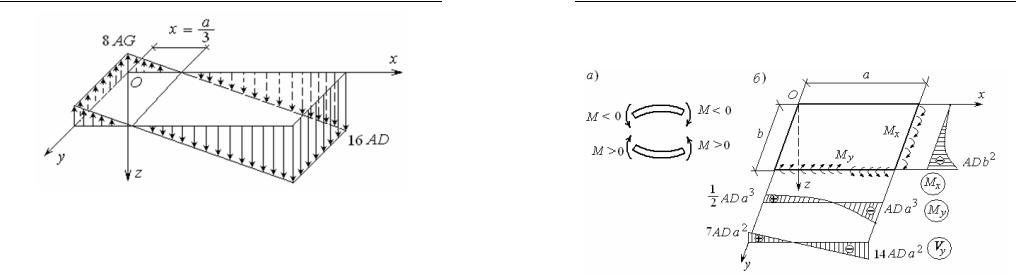
Интенсивность поверхностной нагрузки (5.33), удовлетворяющая дифференциальному уравнению (5.18), по оси y постоянна, а вдоль оси x она изменяется по линейному закону (рис. 37). Положительная интенсивность q поверхностной нагрузки совпадаетс направлением оси z , т. е. направлена вниз, а отрицательная нагрузка направлена противоположно оси z .
2. Определение граничных условий на контуре плиты
Определим граничные условия, которым подчиняется уравнение прогибов (5.32).
72 |
73 |
Теория упругости. Часть II
Рис. 37
Край BP (x = 0;0 ≤ y ≤ b).
На этом крае, совпадающем с осью y , прогибы w и поворот края плиты относительно оси y с учетом (5.32) и (5.32а) будут равны:
(w) |
|
= 0; |
|
∂w |
= 0. |
x=0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
∂ x x=0 |
|
Следовательно, этот край защемлен. |
|
||||
Край CT (x = a;0 ≤ y ≤ b).
На этом краю прогибы равны нулю, но край плиты поворачивается относительно оси, параллельной оси y , т. е.
(w) |
|
= 0; |
|
∂w |
|
= Aa2 y2 ≠ 0. |
|
||||||
x=a |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x x=a |
|
|
|
|
|
|
|
||
При этом изгибающий момент с учетом (5.32) имеет следующее |
|||||||||||||
выражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 w |
|
|
∂2w |
|
|
|
||
|
|
|
|
|
|
2 +µ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
2 |
|
|||||
(M x )x=a = −D |
∂ x |
|
∂ y |
|
|
||||||||
|
|
|
|
|
|
|
|
|
x=a |
|
|
||
= −D[Ay2 (6x − 2a)+µAx2 (x − a)] |
x=a |
= −4ADy2a ≠ 0. |
(5.34) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, край CT упруго шарнирно оперт.
Вдоль края CT изгибающие моменты M x (5.34) изменяются по параболическому закону. (Правила знаков для изгибающих моментов
Задача 5. Расчет тонких плит при поперечном изгибе
в теории плит (рис. 38, б) и в теории изгиба балок (рис. 38, а) при принятом направлении оси z совпадают.)
Рис. 38
Край BC (y = 0;0 ≤ x ≤ a).
На основании (5.32) и (5.32а) на этом краю прогибы и углы поворотов нормали к краю, параллельной оси y , равны следующим значениям:
(w) |
|
= 0; |
|
∂w |
= 0. |
y=0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
∂ x y=0 |
|
Это означает, что на краю BC имеет место защемление.
Край PT (y = b;0 ≤ x ≤ a).
Подставляя в выражение прогибов w (5.32) и углов поворотов
∂w
∂y относительно оси, параллельнойоси x , значение y = a , получим
(w)y=b = Ax2 (x −a)b2 ≠ 0;
|
∂w |
= 2Ax |
2 |
(x −a)b ≠ 0. |
|
|
|
||
|
|
|
|
|
|
∂ y y=b |
|
|
|
74 |
75 |
Теория упругости. Часть II
Следовательно, край PT свободен от жесткого закрепления. На этом краю могут быть приложены изгибающие моменты M y и при-
веденные поперечные силы Vy . Чтобы уточнить наличие или отсутствие силовых факторов на этом крае, найдем указанные внутренние усилия при (y = b;0 ≤ x ≤ a)в сечении, бесконечно близкому к краю:
|
|
∂2w |
∂2w |
|
|
|
|||
|
|
|
2 +µ |
|
|
2 |
|
= |
|
(M y )y=b = −D |
∂ y |
∂x |
|
|
|||||
|
|
|
|
y=0 |
|
||||
= −2AD[(x3 − a x2 )+µb2 (3x − a)]≠ 0; |
(5.35) |
||||||||
|
∂3w |
|
|
|
∂3w |
|
|
||
(Vy )y=a = −D |
|
+ (2 −µ) |
|
|
|
|
|
= |
|
∂3 y |
|
∂2 x |
|
||||||
|
|
|
|
∂ y y=a |
|
||||
= −4AD(2 −µ)(3x − a) b ≠ 0. |
|
(5.36) |
|||||||
Из (5.35) и (5.36) следует, что по краю PT приложены нагрузки (5.35) и (5.36). Следовательно, край соединен с балкой, поддерживающей плиту и испытывающей изгиб и кручение.
Определим характер распределения и величины изгибающих моментов и приведенных поперечных усилийна краю PT. Призначе-
ниях µ = 0,25 и b = a погонные усилия (5.35), (5.36) примут следующий вид:
|
(M y )y=b=a = − |
1 AD[4x3 −4ax2 +3ax − a3 |
]; |
(5.37) |
|||||
|
|
|
2 |
|
|
|
|
|
|
|
(Vy )y=b=a = −7AD(3x −a). |
|
(5.38) |
||||||
Позначениямпогонныхизгибающихмоментов M y |
и приведен- |
||||||||
ныхпоперечныхусилий Vy (табл. 5.1)построеныэпюрыэтихусилий |
|||||||||
(см. рис. 38). |
|
|
|
|
Таблица 5.1 |
||||
|
|
|
|
|
|
|
|||
|
Величины My |
и Vy накраюPT плиты |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
|
0,5а |
|
а |
|
|
|
My (5.37) |
|
0,5ADa3 |
|
0 |
|
ADa3 |
|
|
|
Vy (5.38) |
|
7ADa2 |
|
–3,5ADa2 |
|
–14ADa2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
76 |
|
|
|
|
|
Задача 5. Расчет тонких плит при поперечном изгибе
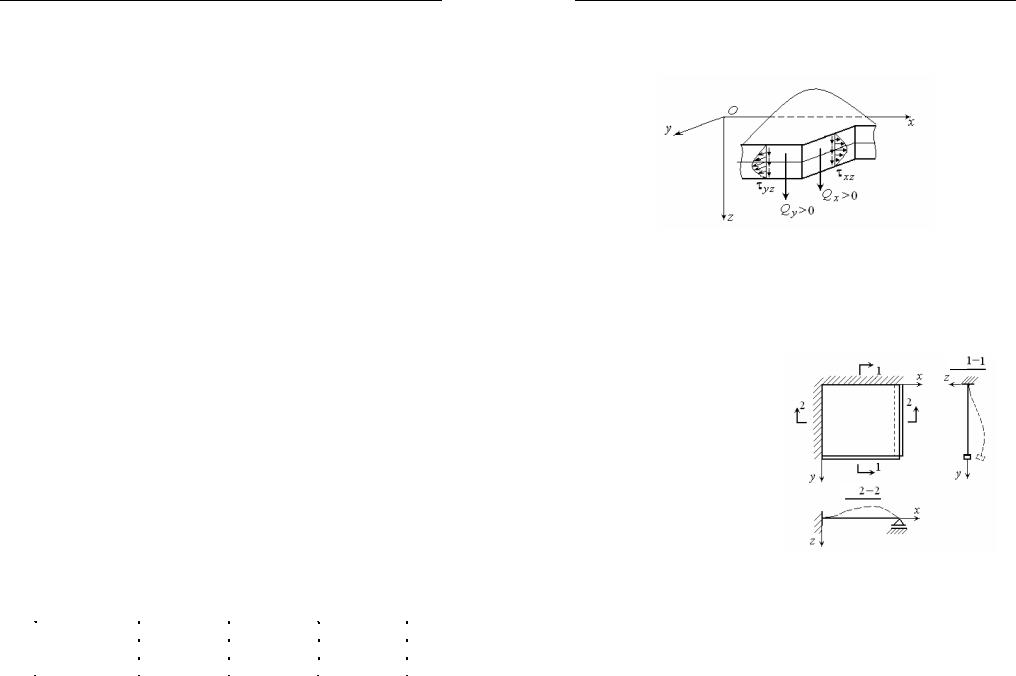
Поперечные усилия Qy (Vy ) и Qy (Vy ) являются равнодейству-
ющими касательных напряжений, и правила знаков аналогичны правилам знаков для касательных напряжений в задаче 1 (рис. 39).
Рис. 39
НаэтомрисункепогонныепоперечныеусилияQy (Vy ) иQy (Vy )
имеют знак «плюс» и направлены вдоль положительной координатной оси z.
Проанализируем характер изогнутойсрединнойповерхно- По сти плиты. Из выражения для прогибов (5.32) видно, что при
0 < x < a все прогибы будут иметь знак «минус». Следова-
тельно, они откладываются от
координатной плоскости xy |
По |
вверх в направлении отрица- |
|
тельной оси z . |
|
На рис. 40 показана пунк- |
|
тирной линией изогнутая сре- |
Рис. 40 |
динная поверхность плиты, со- |
|
ответствующаянайденнымвне- |
Рис. 40 |
|
шним нагрузкам и закреплениям на контуре плиты.
Точкаперегибаизогнутойсрединнойповерхностинаходитсятам, где w′′ по направлению оси x равна нулю, т. е.
77
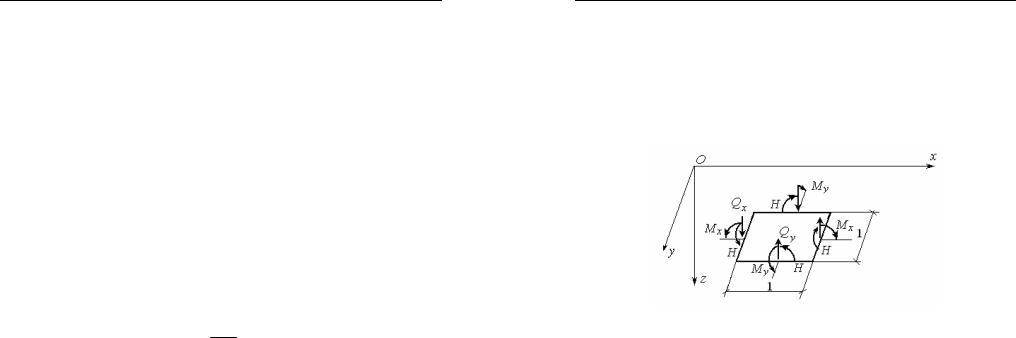
Теория упругости. Часть II
∂2w |
= A(6x − 2a)y = 0. |
(5.39) |
|
∂x2 |
|||
|
|
Уравнение (5.39) обращается в нуль призначении x = a /3, и положение точки перегиба не зависит от координаты y .
3. Определение погонных усилий в окрестности заданной точки
Вначале найдем погонные внутренние усилия (5.12)–(5.16), используя функцию прогибов w (5.32):
• погонные изгибающие моменты
|
∂2w |
|
∂2 w |
|
||
M x = −D |
|
+µ |
|
|
= |
|
∂ x2 |
∂ y2 |
|||||
|
|
|
|
|||
= −2AD[(3x −a)y2 +µx2 (x −a)];
∂2w ∂2w
=−D ∂ y2 ∂ x2
=−2AD [x2 (x −a)+µ(3x − a)y2 ];
•погонный крутящий моментM y +µ =
H = −D(1−µ) |
|
∂2w |
= −2AD(1−µ)(3x2 |
− 2ax)y; |
||||
|
|
|
||||||
|
|
|
∂x ∂ y |
|
||||
• погонные поперечные усилия |
|
|||||||
Qx = −D |
∂ |
|
( 2w) = −2AD(3y2 +3x2 − 2ax); |
|||||
∂ x |
||||||||
|
|
|
|
|
|
|||
Qy = −D |
|
∂ |
( 2w) = −4AD(3x −a)y. |
|||||
|
|
|||||||
|
|
|
|
∂ y |
|
|||
Затем определим погонные усилия в окрестности точки K , на-
пример, с координатами x = 0,5a, y = 0,5b . (Координаты точки указанывисходныхданныхзадачи.)Приэтом,как ивпредыдущемпункте решения задачи, примем, что b = a иµ = 0,25. Тогда
Задача 5. Расчет тонких плит при поперечном изгибе
M x = − |
|
63 |
|
ADa3; M y = − |
|
7 |
ADa3; H = |
|
3 |
ADa3; |
|
128 |
16 |
16 |
|||||||||
|
|
|
(5.40) |
||||||||
|
|
|
|
Qx = −ADa2 ; |
|
Qy = −ADa2. |
|
|
|||
|
|
|
|
|
|
|
|
||||
Внутренние погонные усилия (5.40) в окрестности точки K показаны на рис. 41.
Рис. 41
Для оценкипрочности вначале нужно найтинаибольшие погонныеусилия, азатемопределитьвопасныхточкахнормальныеикасательные напряжения по формулам (5.17).
78 |
79 |
