
Teoria_uprugosti_Ch1_Ledovskoy_12
.pdf
Министерство образования и науки Российской Федерации
Санкт-Петербургский государственный архитектурно-строительный университет
И. В. ЛЕДОВСКОЙ, В. В. РОЩИН, О. Б. ХАЛЕЦКАЯ, Г. С. ШУЛЬМАН
ТЕОРИЯУПРУГОСТИ
Учебно-методическое пособие
Часть I
Санкт-Петербург
2012
1

Теория упругости. Часть I
УДК539.3/8(07)
Рецензенты:
д-р техн. наук, профессор В. Б. Шпильман (СПбГПУ); канд. техн. наук, доцент Н. Б. Левченко (СПбГАСУ)
Ледовской, И. В.
Теория упругости: учеб.-метод. пособие. В 2 ч. Ч. I / И. В. Ледовской [и др.]; СПбГАСУ. – СПб., 2011. – 48 с.
ISBN 978-5-9227-0344-4
Пособие состоит из двух частей: в первой представлены тексты задач курсовой работы, во второй – методические указания по их решению.
Предназначено для выполнения курсовой работы студентами, обучающимися по специальностям 270205 – автомобильные дороги и аэродромы и 270201 – мосты и тоннели, а также может быть использовано студентами других строительных специальностей при изучении основ теории упругости.
Табл. 9. Ил. 11.
РекомендованоРедакционно-издательскимсоветомСПбГАСУ в качестве учебного пособия.
ISBN978-5-9227-0344-4 |
И. В. Ледовской, В. В. Рощин, |
|
О. Б. Халецкая, Г. С. Шульман, 2012 |
|
Санкт-Петербургский государственный |
|
архитектурно-строительный университет, 2012 |
Предисловие
Курсовая работа по теории упругости ориентирована на начальное изучение данной учебной дисциплины. Предлагаемое учебнометодическое пособие состоит из двух частей: в первой содержатся тексты задач курсовой работы, а во второй – методические указания по решению этих задач.
Учебныйматериал,использованныйвпособии,основаннаопыте преподавания этой дисциплины на кафедре сопротивления материалов СПбГАСУ. Более подробное изложение теории упругости приводится в ряде учебников, список которых приведен в конце второй части пособия.
В разных учебниках исправочных пособиях по теории упругости используются различные обозначения для перемещений, деформации и напряжений, поэтому в данном пособии приведена система обозначений, которая рекомендуется студентам при выполнении указанной работы.
Перед выполнением курсовой работы рекомендуется ответить на вопросы по самоконтролю.
Каждыйстудентполучаетиндивидуальныйшифрзаданияупреподавателяидолженпредставитькурсовуюработудоэкзамена(зачета) в установленные сроки. В зависимости от особенностей специальности студентов набор задач может быть изменен.
2 |
3 |
Теория упругости. Часть I
Принятые обозначения
Студентам до решения задач рекомендуется внимательно ознакомиться с обозначениями, принятыми в курсовой работе.
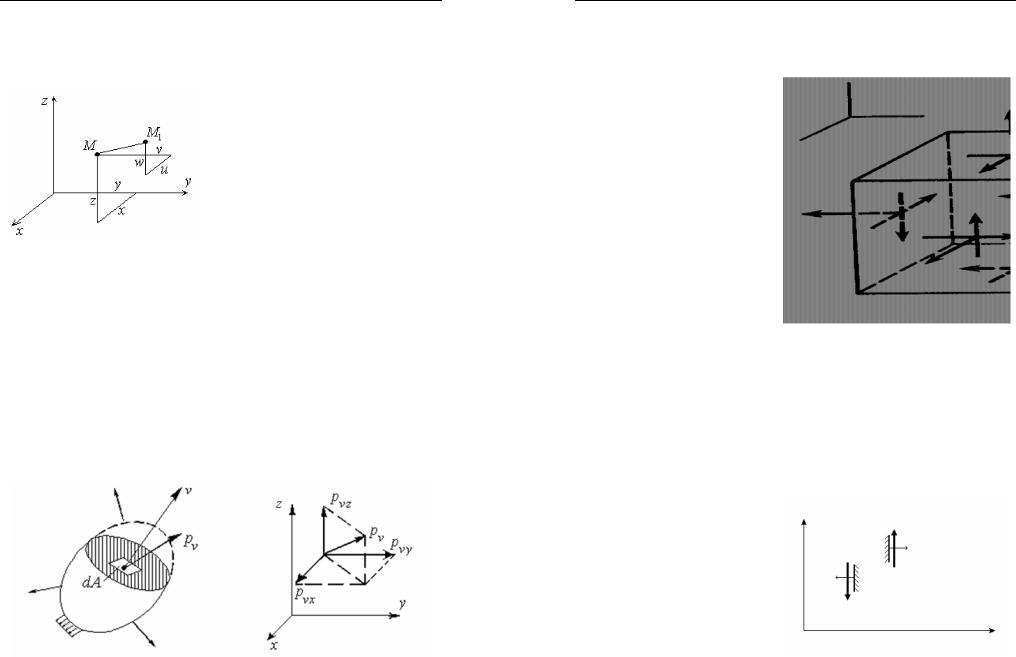
Деформация тела связана сперемещениямиеготочек.Вектор, соединяющийположениянекоторой точки до и после деформации, обозначенныеМ иМ1 (рис.1),называется ее полным перемещением. Составляющие вектора перемещения по осямx,y,z обозначаютсясоответственно u, v иw.
Таким образом, в результате деформаций тела точка М с координатами x, y, z переместится в положение М1 с координатами
x1 = x +u, y1 = y + v, z1 = z + w.
Мерой внутренних сил в сечении тела на площадке dA с внешнейнормалью ν являетсяполное напряжение pν (рис. 2) спроекция-
ми pνx , pνy и pνz , удовлетворяющими соотношению pν2 = pν2x + pν2y + pν2z.
Проекции pνx , pνy и pνz считаются положительными, если их направление совпадает с направлениями осей x, y, z (рис. 3).
Рис. 2 |
Рис. 3 |
Принятые обозначения
Чтобы полностью описать напряженное состояние в точке тела, шестью сечениями выделим в окрестностях этой точки элементарный объем в виде прямоугольного параллелепипеда (рис. 4).
Полное напряжение на |
|
|
z |
|
|
|
|
каждойграниможет бытьраз- |
|
|
|
|
|
|
|
ложено на три составляющие: |
|
|
x |
σz |
|
|
|
одну по нормали к площадке |
|
y |
|
|
|
|
|
и две в плоскости сечения. |
|
|
|
τzx |
σy |
||
Нормальные напряже- |
|
|
|
τzy |
|
|
|
ния, действующие по граням |
|
|
τxy |
|
|
τxz |
|
|
|
τ |
|
|
|||
с внешними нормалями |
|
|
|
yx |
|
|
|
|
|
|
τyz |
|
|
|
|
x, y, z , обозначим буквой σ |
σ |
x |
|
τ |
|
σx |
|
ссоответствующимииндекса- |
|
|
τ |
yz |
τxy |
|
|
|
|
τxz |
yx |
|
|
||
ми (σx ,σy ,σz ). |
|
|
|
τzy |
|
|
|
|
|
σy |
τ |
|
|
||
Касательныенапряжения |
|
|
|
|
|
||
|
|
|
zx |
|
|
|
|
|
|
|
|
|
|
|
|
обозначим буквой τ с двумя |
σz |
|
индексами.Первыйиндекссо- |
||
|
||
ответствует оси, перпендику- |
Рис. 4 |
|
лярной площадке, а второй – |
||
|
||
оси, вдоль которой направлен вектор τ. |
|
Таким образом, τxy , τxz – касательные напряжения на площад-
ке, перпендикулярной оси, действующие вдоль осей y и z; τyx , τyz – напряжениянаплощадке,перпендикулярнойосиy,действующиевдоль осейxиz; τzx , τzy –напряжениянаплощадке,перпендикулярнойосиz,
действующие вдоль осей x и y. |
|
|
|
Растягивающие нормаль- |
j |
|
|
ные напряжения будем считать |
|
τij |
> 0 (ν ↑↑ i) |
положительными,сжимающие– |
|
|
ν |
отрицательными. |
|
ν |
|
Правило знаков для каса- |
|
|
|
тельных напряжений показано |
|
τij > 0 (ν ↑↓ i) |
|
на рис. 5. |
|
|
|
|
|
|
|
Если внешняя нормаль |
|
|
i |
к площадке совпадает по на- |
|
|
|
|
Рис. 5 |
|
|
правлениюсосьюi,тоположи- |
|
|
|
|
|
|
4 |
5 |
Теория упругости. Часть I
тельное касательное напряжение совпадаетпо направлению с осью j. Если внешняя нормаль к площадке направлена противоположно направлению оси i, то положительное касательное напряжение направлено противоположно оси j.
Например, на гранях параллелепипеда, показанного на рис. 4, действуют только положительные нормальные и касательные напряжения.
Для касательных напряжений справедлив закон парности:
τij = τji .
Совокупность напряжений на трех взаимно перпендикулярных площадках
|
σx |
τxy |
τxz |
|
|
|
|||
|
τyx |
σy |
τyz |
|
|
τzx |
τzy |
σz |
|
|
|
называется тензором напряжений, представляющим собой математический объект, более общий, чем вектор. Компоненты тензора напряжений полностью определяют напряженное состояние тела в точке. Это означает, что, зная эти компоненты, можно определить напряженияналюбойплощадке,проходящейчерезрассматриваемуюточкутела.
Для определения деформированного состояния в точке введем шесть компонентов деформации, показанных на рис. 6 и 7.
|
z |
|
z |
z |
|
dy |
|
εz dz = ∆dz |
|
|
|
|
|
|
dz |
x |
|
x |
x |
|
dx |
|
εydy = ∆dy |
|
y |
εxdx = ∆dx |
y |
y |
|
|
|
|||
|
|
|
Рис. 6 |
|
Три относительные продольные деформации определяют удлинения ребер элементарного параллелепипеда в направлении координатных осей без искажения прямых углов между ними (см. рис. 6):
εx = |
∆dx |
; εy = |
∆dy |
; εz = |
∆dz |
. |
dx |
dy |
|
||||
|
|
|
dz |
|||
Принятые обозначения
z |
z |
|
|
z |
γxy |
|
|
|
|
|
|
γyz |
|
|
|
x |
x |
|
x |
|
|
|
|
|
y |
y |
|
y |
γzx |
|
|
|
|
Рис. 7
Здесь ∆dx, ∆dy, ∆dz – абсолютные продольные или линейные деформации.
Индекс в обозначении линейнойдеформации указывает ось, параллельно которой происходит эта деформация. Положительные деформации соответствуют растяжению (удлинению ребер параллелепипеда), отрицательные – сжатию. Три относительные угловые де-
формацииилидеформациисдвига γxy , γyz , γzx определяютизменения углов между ребрами параллелепипеда (см. рис. 7). Индексы указывают на координатную плоскость, в которой происходит изменение прямого угла между ребрами параллелепипеда. Деформация сдвига является положительной, если в процессе деформации прямой угол, образованный двумя отрезками, проведенными из одной точки в направлениикоординатныхосей, уменьшается.Впротивномслучаедеформация считается отрицательной.
В результате деформации объем элементарного параллелепипе-
да dV получает приращение ∆dV . Величина εV = ∆ddVV называется
относительной объемной деформацией. При малых деформациях величина εV может быть определена по формуле
εV = εx +εy +εz .
Для определения деформационных свойств линейно упругого однородного изотропного материала используем модуль упругости первого рода (модуль Юнга) E, модуль упругости второго рода (модуль сдвига) G и коэффициент Пуассона µ, связанные между собой
соотношением G = 2(1Е+μ).
6 |
7 |

Теория упругости. Часть I
Для определения внешних нагрузок введем следующие обозначения: X ,Y, Z – проекции интенсивности объемных нагрузок на координатные оси x, y, z (т. е. силы, действующие на единицу объема тела); X ,Y , Z – проекции интенсивности поверхностных нагрузок на координатные оси x, y, z (т. е. силы, действующие на единицу площади поверхности тела).
Вопросы для самоконтроля
I.Теория напряжений
1.Какие виды напряжений различают и как онинаправлены по отношению к площадке, выделенной в сечении тела?
2.Каковы правила знаков для нормальных и касательных напряжений?
3.Сформулируйте закон парности касательных напряжений.
4.Сколько компонентов напряжений полностью определяют напряженное состояние тела в точке?
5.Какие напряжения называют главными?
6.Напишите выражения для определения инвариантов напряженного состояния.
7.Какому напряженному состоянию соответствуют условия
равенства нулю третьего инварианта (I3 = 0 ), третьего и второго ин-
3= I2 = 0 )?
8.Какопределяютсянормальныенапряжениянапроизвольной площадке, если известны главные напряжения σ1, σ2 , σ3 ?
9.Какопределяютсякасательныенапряжениянапроизвольнойвариантов (I
площадке, если известны главные напряжения σ1, σ2 , σ3 ?
10.Какиедопущениябылииспользованыпривыводедифференциальных равнений равновесия (уравнения Навье)?
11.Напишите уравнения равновесия на поверхности тела.
II. Теория деформаций
1.Какие различают виды деформаций?
2.Какие правила знаков для относительной линейной и угловой деформации приняты в теории упругости?
Вопросы для самоконтроля
3.Сколько компонентов деформации полностью определяют деформированное состояние тела в точке?
4.Напишите кинематические соотношения Коши.
5.Какиедопущения былииспользованы привыводе соотношений Коши?
III.ЗаконГука
1.Напишите обобщенный закон Гука, выразив компоненты деформации через компоненты напряжений.
2.Напишите обобщенный закон Гука, выразив компоненты напряжений через компоненты деформации.
3.Напишите закон Гука для объемной относительной дефор-
мации.
IV. Методырешения задач теории упругости
1.Какиеуравнениявходятвполнуюсистемууравненийтеории упругости?
2.Скольконеизвестныхфункцийвходитвполнуюсистемууравнений теории упругости?
3.Какие граничные условия используются при решении задач теории упругости?
4.В чем особенности решения задачи теории упругости прямым, обратным и полуобратным методом?
V.Плоская задача теории упругости
1.Что понимают под плоской деформацией? Какие перемещения возникают при плоской деформации?
2.Чтопонимаютподплоскимнапряженнымсостоянием?Вчем отличие плоского напряженного состояния от плоской деформации?
3.Сколько неизвестных функций входит в систему уравнений плоской задачи теории упругости?
4.Напишите систему уравнений для плоской задачи теории упругости в напряжениях.
8 |
9 |

Теория упругости. Часть I
5.Напишите выражения, связывающие компоненты напряжений с функцией напряжений ϕ.
6.Напишите уравнение совместности деформаций с использованием функции напряжений.
VI. Теориятонких плит
1.Какие плиты называют тонкими?
2.Какие деформации плиты можно считать малыми?
3.Какие допущения используются в теории тонких плит?
4.Напишите выражения для деформаций εx , εy , γxy , выразив их через прогибы срединной поверхности плиты.
5.Как выражаются погонные поперечные усилия Qx ,Qy через прогибы срединной поверхности?
6. Как выражаются погонные изгибающие моменты M x , M y
икрутящий момент H через прогибы срединной поверхности?
7.Напишите уравнение прогибов срединной поверхности плиты С. Жермен.
Введение
Цель курсовой работы предполагает применение знаний, полученных в процессе изучения теории упругости. Поэтому каждой задаче из курсовой работы должны предшествовать изучение соответствующих разделов курса и ответы на вопросы самоконтроля, приведенныевыше.Самостоятельноеисознательноевыполнениекурсовой работы является необходимым условием готовности студента к зачету (экзамену) по теории упругости.
Исходныеданныедлякаждойзадачистудентопределяетпошифру, выданномуемупреподавателем,ввидетрехзначногочисла(АВС).
Найдем исходные данные для выполнения задачи 1, если, например, выданный шифр задания 230. Буквой A обозначается цифра 2, буквой В – 3, а буквой C – 0. По табл. 1.1 и 1.2 находим:
по букве A: |
σx |
= −20 МПа; |
|
σy = 30 МПа; |
σz = −40 |
МПа; |
||||||||
B: τxy = −30 МПа; |
|
τyz = 40 МПа; |
τzx = −50 |
МПа; |
||||||||||
C: |
l = |
|
1 |
, m = |
1 |
, |
n = |
1 |
, α =120 . |
|
||||
|
|
|
|
|||||||||||
|
|
|
3 |
3 |
|
|||||||||
3 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||
Контрольная работа выполняется на листах белой бумаги формата А4 с одной стороны. Работа может быть оформлена с использованием компьютера или представлена в рукописном варианте. В последнем случае текст работы записывается чернилами, а рисунки выполняютсякарандашом.Вначалекаждойзадачиприводятсяисходные данные и расчетная схема.
Решение сопровождается заголовками, краткими пояснениями к пунктам задачи и необходимыми чертежами.
Получив проверенную преподавателем работу, студент должен исправить внейуказанныеошибки, исправленияпредставитьначистыхлистахбумаги, подшитыхкработе.Запрещаетсявырыватьлисты с замечаниями преподавателя и заменять их новыми.
10 |
11 |

Теория упругости. Часть I
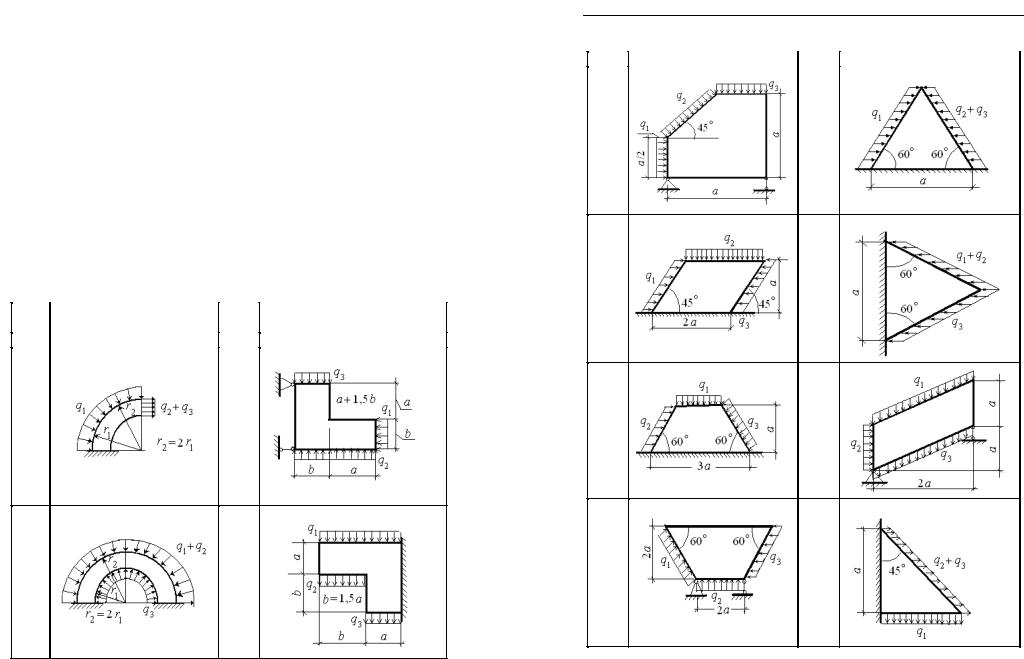
Задача 1. ИССЛЕДОВАНИЕ НАПРЯЖЕННОДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ ТЕЛА
Напряжения, действующие по граням элементарного параллелепипеда, даны в табл. 1.1. Требуется:
1.Показать эти напряжения на чертеже.
2.Определить:
•полное,нормальноеикасательноенапряжения,действующие по наклонной площадке АВСD (угол α указан в табл. 1.2);
•проекцию касательного напряжения, действующего по координатнойплощадке, накоторойрасположенотрезокВС,нанаправление этого отрезка;
•величиныглавныхнапряженийиположениеглавнойплощад-
ки, по которой действует напряжение σ1.
3. ПримодулеупругостиE=2,105 МПаикоэффициентеПуассона µ= 0,25 определить:
•линейную деформацию в направлении, заданном направляющими косинусами l, m, n , которые указаны в табл. 1.2;
•угол сдвига между направлениями ВА и ВС;
•объемнуюдеформациювисследуемойточкенапряженноготела.
Таблица 1.1
Напряжениявисследуемойточке,МПа
Буква |
Напряжение |
Буква |
Напряжение |
|||||
A |
σx |
σy |
σz |
B |
τxy |
τyz |
τzx |
|
0 |
0 |
10 |
20 |
0 |
0 |
10 |
20 |
|
1 |
–10 |
–20 |
30 |
1 |
–10 |
20 |
–30 |
|
2 |
–20 |
30 |
–40 |
2 |
–20 |
–30 |
40 |
|
3 |
–30 |
40 |
50 |
3 |
–30 |
40 |
–50 |
|
4 |
–40 |
–50 |
60 |
4 |
–40 |
50 |
60 |
|
5 |
–50 |
60 |
–70 |
5 |
–50 |
–60 |
70 |
|
6 |
60 |
70 |
–80 |
6 |
60 |
70 |
80 |
|
7 |
70 |
–80 |
–90 |
7 |
70 |
–80 |
90 |
|
8 |
80 |
90 |
–100 |
8 |
80 |
–90 |
–100 |
|
9 |
90 |
–100 |
110 |
9 |
90 |
–100 |
–110 |
|
Задача 1. Исследование напряженно-деформированного состояния в точке тела
Таблица 1.2
Исходные данные к задаче 1
Бук- |
|
|
|
Направляющие |
Угол |
Положение площадки |
||||||||||||||||||||
ва |
|
|
|
|
|
косинусы |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
α, град |
ABCD |
||||||||||||||
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
l |
|
m |
|
|
n |
||||||||||||||||||||
0 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
120 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
150 |
|
|||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
2 |
|
|
|
|
|
|
|
− 1 |
30 |
|
|||||||||||
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
|
|
|
|
|
|
|
|
|
7 |
|
|
|
60 |
|
|||||||||||
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
60 |
|
||||||||||
4 |
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5 |
|
|
|
2 |
|
|
|
|
|
|
6 |
|
|
|
30 |
|
||||||||||
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
5 |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
60 |
|
|||||||||
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7 |
|
|
|
|
|
|
|
− |
11 |
45 |
|
|||||||||||||||
4 |
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
8 |
|
− |
2 |
|
|
|
|
|
|
|
120 |
|
||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
9 |
|
6 |
|
− |
|
6 |
|
|
|
|
|
|
|
150 |
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
13 |
Теория упругости. Часть I
Задача 2. ПОСТАНОВКА КИНЕМАТИЧЕСКИХ
ИСТАТИЧЕСКИХ ГРАНИЧНЫХ УСЛОВИЙ
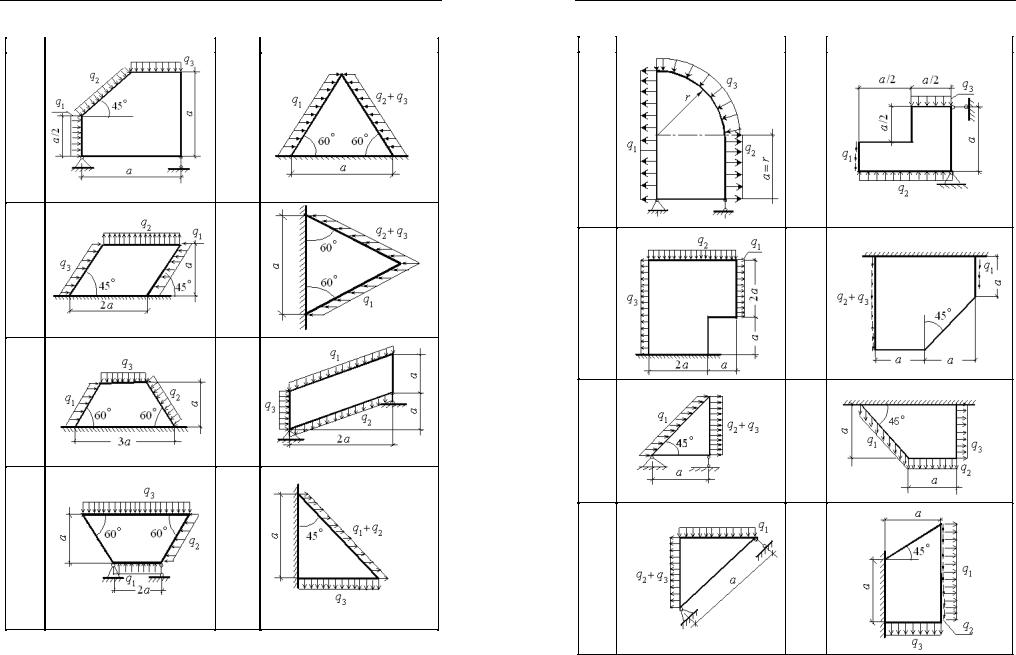
Кпластинке единичной толщины приложены по контуру внешниенагрузки,действующиепараллельносрединнойплоскостипластинки и распределенные равномерно по ее толщине (табл. 2.1). Пластинка будет находиться в плоском напряженном состоянии, т. е. по площадкам, параллельным боковым поверхностям, напряжения равны нулю. Данные о величинах приложенных нагрузок определяются по табл. 2.2.
Требуется сформулировать статические и кинематические граничные условия на контуре пластинки.
Таблица 2.1
Исходные данные к задаче 2
Буквы |
Схема нагружения |
Буквы |
Схема нагружения |
AB |
пластинки |
AB |
пластинки |
1 |
2 |
3 |
4 |
00÷02 |
|
05÷07 |
|
03÷04 |
08÷10 |
Задача 2. Постановка кинематических и статических граничных условий
|
|
|
Продолжение табл. 2.1 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
11÷12 |
|
19÷21 |
|
|
13÷14 |
22÷24 |
15÷16 |
25÷27 |
17÷18 |
28÷30 |
14 |
15 |
Теория упругости. Часть I
|
|
|
Продолжение табл. 2.1 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
31÷32 |
|
39÷41 |
|
|
33÷34 |
42÷44 |
35÷36 |
45÷47 |
37÷38 |
48÷50 |
Задача 2. Постановка кинематических и статических граничных условий
|
|
|
Продолжение табл. 2.1 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
51÷52 |
|
59÷61 |
|
|
53÷54 |
62÷64 |
55÷56 |
65÷67 |
57÷58 |
68÷70 |
16 |
17 |

Теория упругости. Часть I
|
|
|
Продолжение табл. 2.1 |
|
|
|
|
1 |
2 |
3 |
4 |
71÷72 |
|
79÷81 |
|
73÷74 |
82÷84 |
75÷76 |
85÷87 |
77÷78 |
88÷90 |
Задача 2. Постановка кинематических и статических граничных условий
|
|
|
Окончание табл. 2.1 |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
91÷92 |
|
95÷97 |
|
|
93÷94 |
98÷99 |
Таблица 2.2
Исходные данные о величине нагрузок к задаче 2
|
Буква |
|
Нагрузка, кН/м2 |
|
||
|
|
|
||||
|
С |
|
|
|
|
|
|
q1 q |
|
2 q |
|
3 |
|
|
0 |
2 |
|
2 |
|
0 |
|
|
|
||||
|
1 |
3 |
|
0 |
|
0 |
|
2 |
0 |
|
1 |
|
1 |
|
3 |
3 |
|
3 |
|
0 |
|
4 |
2 |
|
0 |
|
3 |
|
5 |
0 |
|
2 |
|
3 |
|
|
|
||||
|
6 |
1 |
|
1 |
|
0 |
|
|
|
||||
|
7 |
1 |
|
0 |
|
1 |
|
|
|
||||
|
8 |
0 |
|
1 |
|
2 |
|
9 |
2 |
|
0 |
|
2 |
18 |
19 |
