Teoria_uprugosti_Ch2_Ledovskoy_12

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ydy = M = M0 ;

.pdf

Скачиваний:

219

Добавлен:

29.03.2015

Размер:

650.8 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Теория упругости. Часть II

постоянные коэффициенты a2 ,b3, d3, d5 определимизграничныхус-

ловий на контуре полосы (b).

Рассмотрим статические граничные условия по граням полосы

(см. рис. 19):

• верхняя грань:

y = −c при − L ≤ x ≤ L;		l1 = 0;	m1	= −1;
				(4.31)
X = 0;	Y	= q;		(4.31)
X = 0;	Y	= q;
• нижняя грань:
y = c при − L ≤ x ≤ L;		l2 = 0;	m2	=1;
				(4.32)
X = 0;	Y	= 0.		(4.32)
X = 0;	Y	= 0.

Подставляя в граничные статические условия (4.20) компоненты напряжения (4.30) с учетом (4.31) и (4.32), получим

(σ

+ τ

m )

;

y=−c

−b c −

)(−1) = q;

x 1

(а)

(τyxl1 + σy m1 )y=−c = Y ;

(−b c − d

c3 )x(−1) = 0,

(σ

+ τ

m )

;

y=+c

+b c +

)(+1) =

x 1

(б)

+ σy m1 )y=+c = Y ;

(τyxl1

(+b c + d

c3 )x(+1) = 0.

Решая систему уравнений (a) и (б), находим

= − q ;

b3 =

3 q ;

d5 = −

3 q .

(4.33)

4 c

4 c3

Если в (4.30) вместо коэффициентов a2 , b3 , d5 подставить их

значения в виде (4.33), то выражения для напряжений будут иметь следующий вид:

= d

y −

q x2 y +

y3;

4c3

2c3

σy = − q

+ 3q y −

2 q

;

(4.34)

4c3

τxy = −

3q x +

x y2.

4c3

Задача 4. Плоская задача теории упругости. Функция напряжений

По условию задачи на каждом из торцов полосы действуют только касательныенагрузки,равнодействующиекоторыхравныqc L (рис.20). Граничные условия на правом торце:

при x = L и − c ≤ y ≤ +c l3 =1, m3 = 0;				(4.35)
			≠ 0.	(4.36)
	X	= 0, Y

Из граничных статических условий (4.20) с учетом (4.34)–(4.36) найдем выражения для интенсивности поверхностных нагрузок:

=[σ

l + τ

m ]

=[σ

]

= d

y −

L2 y +

y3;

4c3

2 c3

x=L

= −3q L +

L y2.

(4.37)

=[τ

l +σ

m ]

x=L

=[τ

]

x=L

4c3

Из решения (4.37) следует, что, во-первых, касательные нагрузки изменяются по параболическому закону на торце; во-вторых, имеют место и нормальные поверхностные нагрузки.

	Сен-Венаном было установлено,
	Сен-Венаном было установлено,
	что изменение распределения нагрузки
	на торце стержня при одном и том же
	главном векторе и главном моменте вне-
	шних сил приводит лишь к появлению
	другихместныхнапряженийвблизитор-
	цовстержня,анапряжениявдалиотмес-
	та приложения нагрузки остаются почти	Рис. 20
	неизменными [1, 2, 4].	Рис. 20
	неизменными [1, 2, 4].
	В связи с этим предлагается
	вместо точных граничных условий
	использовать интегральные гранич-
	ные условия из табл. 4.2 (см. ч. I
	учебно-методического пособия). На
	правом торце показаны равнодей-
	ствующие поверхностных внешних
	сил,имеющиеположительныезначе-
	ния.Соотношениямеждуэтимирав-
	нодействующими и интенсивностя-
	миповерхностныхсил(рис.21)име-
	ют следующий вид:	Рис. 21
	41

Теория упругости. Часть II

∫X dA = +∫cX dy = P1;

(A) −c

∫		dA y =	+∫c		y dy = M ;
	X			X		(4.38)
(A)			−c

∫Y dA = ∫Y dy = P2 .

(A) −c

В даннойзадаче равнодействующиеповерхностныхнагрузокна правом торце (см. рис. 19) имеют следующие значения:

P1 = 0; M = 0; P2 = −qL.

(4.39)

Рассмотриминтегральныеусловия(4.38)сучетом(4.37)и(4.39). Первое условие (4.38) имеет вид

∫ d3 y −

L y +

dy =

2 c

−c

q y4

+h /2

= d3

−

= 0.

(4.40)

2 c

−h /2

Соотношение (4.40) превращается в тождество при любом значении d3 , так как переменная y имеет четные степени.

Второе интегральное условие (4.38) получает следующее выражение:

∫

d3 y

−

L y

dy =

−c

q y5

= d3

−

= 0,

4c3

2 c3 5

−c

откуда

d3 =

3 qL2

−

3 q .

(4.41)

4 c3

10 c

Задача 4. Плоская задача теории упругости. Функция напряжений

Наконец, третье интегральное условие (4.38) превращается в тождество

− Lq =

−

L +

dy =

4c3

−∫c

= −

Ly +

= Lq −

= −Lq.

−c

Если в выражение для σx (4.37) вместо коэффициента d3 под-

ставим его значение в виде (4.41), то получим

3 q 2

σx =

− x

]y +

−

y .

(4.42)

Те же результаты получаются из интегральных условий на левом торце.

Осевой момент инерции поперечного сечения будет

Iz =112h3 = 23c3 (см. рис. 21). Тогда окончательные выражения для напряжений (4.34) с учетом (4.42) будут

σx =

[L2 − x

2 ]y

−

;

c2 y

2Iz

2c3

2Iz

σy = −

−c

y +

;

(4.43)

2Iz

τxy = −

[c2 − y2 ].

2Iz

Сравним полученное решение с решением методами сопротивления материалов.

4.4.3. Решение задачи методами сопротивления материалов

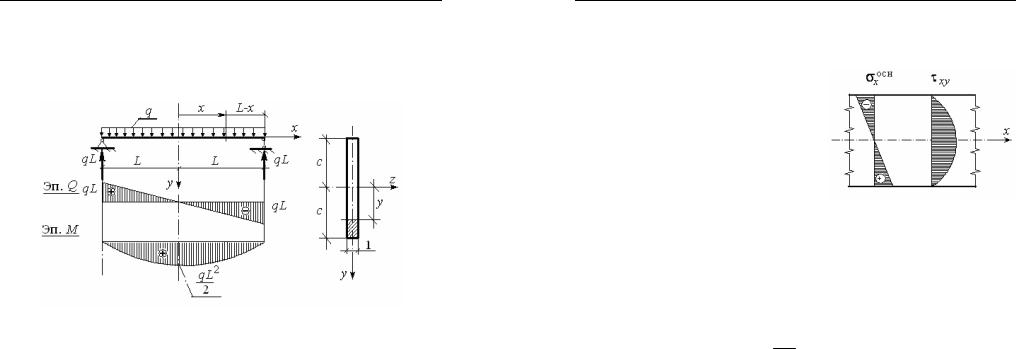
Рассмотрим решение задачи об изгибе балки равномерно распределенной нагрузкойэлементарными методамисопротивления материалов (см. рис. 21).

Теория упругости. Часть II

Из курса сопротивления материалов известно, что

σx =	M	z y; σy = 0; τxy = −	QS отс	(4.44)
			z .
	Iz		Iz

Рис. 22

Методами сопротивления материалов найдем внутренние усилия в поперечном сечении балки, показанной на рис. 22:

• изгибающий момент

M z = qL(L − x)− q2 (L − x)2 = q2 [L2 − x2 ];

• поперечная сила

Q= −qL + q(L − x)= −qx;

•статический момент отсеченной части сечения

Sz =1(c − y) y + 1		(c − y)	= 1 (c2 − y2 ).
	2		2

Следовательно,длянапряжений(4.44)получимследующиеокончательные формулы:

	q		2				qx	[c2 − y2 ].
σx =		L		− x2	y; σy = 0;	τxy = −			(4.45)

	2Iz		4				2Iz

Задача 4. Плоская задача теории упругости. Функция напряжений

4.4.4. Анализ полученных решений

Сравнивая выражения для напряжений σx ,σy , τxy , полученные

методами теорииупругости и сопротивленияматериалов,можносделать следующие выводы:

1.Касательные напряжения

τxy , определяемые методами сопро-

тивления материалов и теории упругости,полностьюсовпадают.Распре- Рис. 23 деление этих напряжений по высоте поперечного сечения показано на рис. 23.

2. Выражение для напряжения σx , полученное методами тео-

рии упругости, состоит из двух слагаемых:

• первое слагаемое (основное)

σоснx = 2qIz [L2 − x2 ]y

совпадает с напряжением σx , полученным элементарной теорией из-

гиба (см. рис. 23);

• второе слагаемое (дополнительное)

доп		q	2		3		2		2			3q		1		3		1		2
σx	=			y		−		c		y	=				y		−		c		y	(4.46)
σx	=		3	y		−	5	c		y	=	2c	3	3	y		−	5	c		y	(4.46)
		2Iz	3				5					2c		3				5

представляет поправку, которая не зависит от координаты x (рис. 24). Эта поправка отсутствует в элементарной теории изгиба, которая предполагает отсутствие надавливания волокон друг на друга. Между тем из решения теории упругости (4.43) видно, что между

этими волокнами действуют сжимающие напряжения σy . Распреде-

ление сжимающих напряжений σy по высоте полосы, показанное на рис. 24, не зависит от продольной координаты x.

Теория упругости. Часть II

	σy	q			доп
		q			σx
c		27
2			32 q		–0,2 q
c		+0,087 q
2		+0,087 q
c		0,5 q
2		0,5 q
c			5	q +0,2 q	–0,087 q
c		32		q +0,2 q
2
2
		Рис. 24

Оценим влияние σдопx

на

(σx )max ,

которое возникает при

x = 0; y = c :

(σx )max

−0]c +

−

2I z

qL2

q(5−3)c3

= M max

1 +

(4.47)

2 I z

15I z

где

I z

;

M max = qL2 .

Изтабл.4.1видно,чтовлияние σдопx

при

< 1

становитсямень-

ше 3 % и им можно пренебречь.

Таблица 4.1

				Влияние 1		+			4 c2		на величину (σх)max вформуле(4.47)

								15		2
								15		L
			c			1						1	1	1
			L				10					4	3	2
1	+		4 c2		1,0027							1,017	1,030	1,067

		15 L2
		15 L2

Таким образом, при расчете балок, длина которых 2L меньше

трех высот h = 2c, решение (4.43) для нормальных напряжений использовать нельзя.

Задача 4. Плоская задача теории упругости. Функция напряжений

3.Полученное решение (4.43) является точным, если по торцам приложены касательные нагрузки, изменяющиеся по параболическому закону, а также взаимно уравновешенные нагрузки, параллельные оси x. Эти нагрузки по способу приложения отличаются от нагрузок, действующих на рассматриваемую балку. Поэтому это решение на основании принципа Сен-Венана пригодно для описания напряженного состояния только в точках, достаточно удаленных от торцов.

4.Найдем влияние на напряжения σx взаимно уравновешенных нагрузок, действующих вдоль оси x, на расстоянии 2c от торца и при длине балки, равной L =10c .

Из выражения σx

(4.43) в точке при x =8c и

y = c найдем:

• основное слагаемое

σоснx

[(10c)2 −(8c)2 ]c =

36c2 =

27q

;

2Iz

4c3

• дополнительное слагаемое или поправка

доп

σx

−

Поправка для напряжений σx за счет учета взаимно уравновешенных сил на торце составляет всего

σдопx	100 % =	1	100 % = 0,74%.
σоснx		5 27

Поэтому влиянием на нормальные напряжения в полосе длиной L =10c взаимно уравновешенных сил, приложенных на торце, уже на расстоянии, равном h = 2c, можно пренебречь.

4.5. Изгиб прямоугольной полосы под действием собственного веса

4.5.1. Постановка задачи

Прямоугольная полоса с узким поперечным сечением опирается шарнирно по концам (рис. 25). Она изгибается под действием соб-

Теория упругости. Часть II

ственного веса с интенсивностью ρ, т. е. на единичный объем в каждой точке тела действуют объемные нагрузки, интенсивность которых равна

X = 0; Y = ρ; Z = 0.

(4.48)

Кроме того, на торцах приложены нагрузки, сводящиеся к парам сил с моментом M0 .

Рис. 25

Полагаем,чтонапряженноесостояниеполосыявляетсяплоским и не изменяется вдоль координаты z . Поэтому ширина сечения поло-

сы по координате z принята равной единице, т. е. b =1.

Требуется определить компоненты напряжений σx ,σy , τxy методами теории упругости и сопротивления материалов.

4.5.2. Решение задачи

Покажем, что задачу о напряжениях в указанной полосе можно решить, используя функцию напряжений ϕ, заданную в виде суммы полиномов:

ϕ =	d			−	1	y5	+	b	x2 y +	d		y3 .	(4.49)
ϕ =		5	y3 x2	−	5	y5	+	3	x2 y +		3	y3 .	(4.49)
	6				5			2		6

Убедимся вначале, что при помощи этой функции можно описывать напряженное состояние полосы без разрывов и трещин. Для этогоподставимфункциюнапряжений ϕ восновноеуравнение(4.26) плоской задачи

∂4ϕ	+ 2	∂4ϕ	+	∂4ϕ	= 0.
∂x4		∂x2∂ y2		∂ y4

Задача 4. Плоская задача теории упругости. Функция напряжений

Производные от функции ϕ, входящие в это уравнение, имеют следующие значения:

∂4ϕ	= 0;	∂4ϕ	= −4d5	y;	∂4ϕ	= 2 d5	y.
∂x4		∂ y4			∂x2∂ y2

Подставим их в уравнение сплошности (4.26) и получим

2 2d5y −4d5y = 0.

Поскольку уравнение сплошности обращается в тождество при любых значениях коэффициентов b3, d3, d5, то функция (4.49) описывает напряженное состояние без разрывов и трещин.

Неизвестныепостоянныекоэффициенты b3, d3, d5 определимиз статических граничных условий на контуре полосы (4.20):

X = σx l + τxy m; Y = τyx l +σy m.

Вначале выразим через функцию ϕ напряжения, входящие в правуючастьграничныхусловий(4.20). Послеподстановкифункции ϕ (4.49) в формулы (4.25) получим:

∂2

= d

y + d

y −

; σ

= b y +

;

∂ y2

∂ x2

τ	xy	= −	∂2ϕ	− X y −Yx = (−b −d				5	y2 )x −ρx =	(4.50)
τ		= −		− X y −Yx = (−b −d					y2 )x −ρx =
			∂ x ∂ y				3
			∂ x ∂ y
				= (−b −d	5	y2	−ρ)x.
				3	5

Постоянные коэффициенты, входящие в выражения (4.50), дол-

жны обеспечить равенство внутренних и внешних сил на контуре полосы. Условием выполнения такого равенства является соблюдение статических граничных условий, в которые кроме напряжений входят направляющие косинусы и интенсивности внешних нагрузок

(см. рис. 31):

на верхней грани: при y = −c;		− L ≤ x ≤ +L;
l1 = 0;	m1 = −1;							= 0;	(4.51)
				X		=Y
на нижней грани: при y = +c;		− L ≤ x ≤ +L;
l2 = 0;	m2 = +1;						= 0.		(4.52)
			X		= Y

Теория упругости. Часть II

Граничныеусловия(4.20)дляверхнейгранисучетом(4.51)имеют следующий вид:

(σ

+ τ

m )

;

(−b3 −d5 c2 −ρ)x(−1) = 0;

y=−c

x 1

(τ

+ σ

m )

;

(−b c −

1 d

c3 )(−1) = 0,

y=−c

yx 1

откуда

= −d

c2 −ρ;

= ρ

;

= −1 d5c2 ;

3ρ

(4.53)

= −

При рассмотрении граничных условий на нижней грани получим те же значения для коэффициентов b3 , d5.

Для напряжений σx ,σy , τxy (4.64) с учетом (4.67) получим следующие выражения:

σx = d3

y −

3ρ

(x2 y

− 2 y3 );

2c2

σy

= ρ y −

y3;

(4.54)

2 c2

τxy = (−

3ρ +

3ρ

y2 )x = −

3ρ

(c2

− y2 )x.

2c2

Чтобыопределить коэффициент d3 , найдеминтенсивностивне-

шних нагрузок

например, на правом торце. Для этого подста-

вим выражения напряжений (4.54) и значения направляющих коси-

нусов внешней нормали l3 = +1;

m3 = 0 в граничные статические

условия (4.20)

3ρ

= (σ

+ τ

)

;

X = (d3 y

−

(L y −

)(+1);

x=L

3ρ

(4.55)

= (τ

+ σ

)

;

x=L

Y = −

− y

)L(+1).

2c2

Задача 4. Плоская задача теории упругости. Функция напряжений

Из выражений (4.55) видно, что по торцу действуют касательные и нормальные внешние нагрузки. Однако при постановке задачи не были заданы законы их распределения (см. рис. 25).

Используя принцип Сен-Венана, вместо точных граничных условийрассмотриминтегральныеграничныеусловия(4.53),которыепри значении x = ±L имеют следующий вид (см. табл. 4.2 пособия, ч. 1,

и рис. 25):

∫X dA = ∫c X dy = P1 = 0;

∫Y dA = ∫c Y dy = P2 = −2ρcL.

(A) −c

В(4.56)былиучтеныправилазнаковдляпроекцийравнодействующих внешних сил на оси x и y, которые были показаны на рис. 20.

Вначале рассмотрим первое интегральное уравнение (4.56) с учетом (4.55):

−c

3ρ

(L2 y −

2 y3 )]dy =

∫

dA = ∫

dy = ∫[d3 y −

2c2

(A)

−c

3ρ

= [d3

−

)]

= 0.

(4.57)

2c2

−c

При четной функции y уравнение (4.57) превращается в тождество при любом значении d3 .

Далее рассмотрим второе интегральное уравнение (4.56):

3ρ

∫[d3 y

−

(L y

−

)]dy =

−c

3ρ

= d3 ∫y

∫y

−

dy +

dy =

−c

2c3

3ρ

2c3

ρ 2c5

= M0.

= d3

−

(4.58)

2c2

Теория упругости. Часть II

Заметим, что осевой момент инерции для прямоугольного попе-

речного сечения при ширине b =1 равен
Iz =	bh3	=	8c3	=	2c3	.	(4.59)
Iz =	12	=	12	=	3	.	(4.59)
	12		12		3
С учетом (4.59) из соотношения (4.58) получим для коэффици-
ента d3 следующее выражение:
d3 =	M 0 +		ρcL2		− 3ρ.		(4.60)
	I z		I z		5

Если в формулудля нормальных напряжений σx из (4.54) вместо коэффициента d3 подставитьеговыражение ввиде(4.60), тополучим:

σx

= (

ρcL2

−

3ρ

) y −

ρc

−

) =

ρc

y +

− x

)y +

−

y).

(4.61)

В выражение (4.61) входят три слагаемых:

• от изгибающих моментов M0

σx =

M 0 y;

I z

• от собственного веса (основное слагаемое)

σоснx = ρIc (L2 − x2 )y;

• от собственного веса (дополнительное слагаемое)

σдопx = cρ2 (y3 − 53 c2 y),

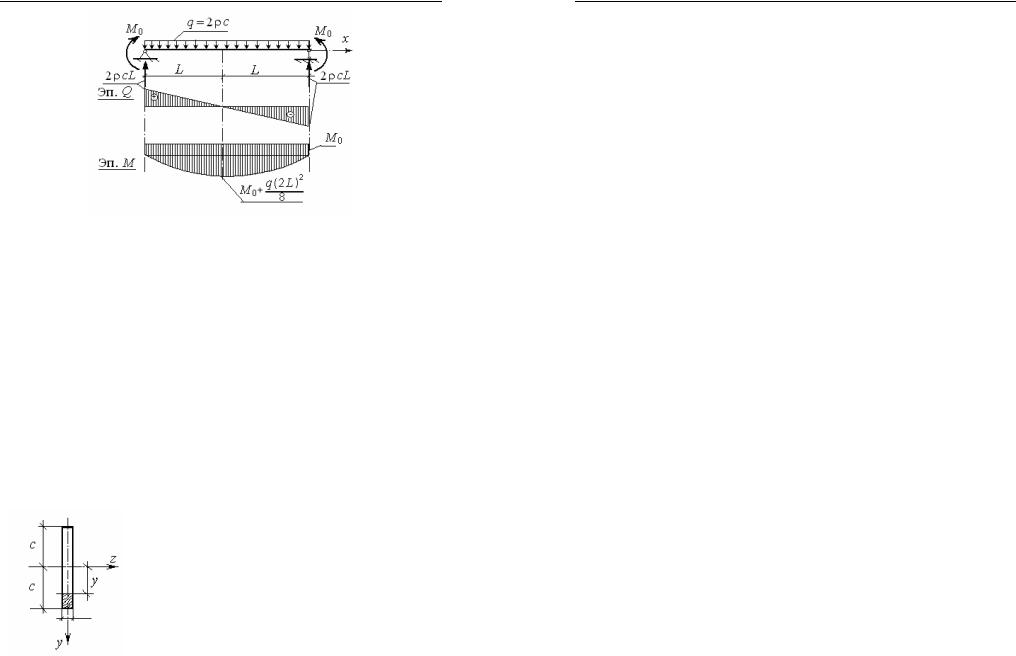
которые в виде эпюр показаны ниже (рис. 26).

НаконецрассмотримтретьеинтегральноеусловиепоСен-Венану из (4.56):

∫Y dA = ∫Y dy = −2ρhL.

(A) −c

Задача 4. Плоская задача теории упругости. Функция напряжений

Рис. 26

Подставляя в это интегральное граничное условие вместо ин-

тенсивности поверхностных касательных нагрузок Y ее выражение из (4.55), получим тождество. Действительно,

3ρ 2

3ρ

∫

−

2 (c

− y ) dy =

−

c y −

−c

2 3ρ

c −

= −2ρcL.

Напряжения σx ,σy , τxy

(4.54) с учетом (4.59)–(4.61) примут

окончательный вид

ρc

σx

y +

− x

)y +

−

y);

σy

ρ y

−

y3;

(4.62)

2c2

τxy = −

ρcx(c2 − y2 )

4.5.3. Решение задачи методами сопротивления материалов

Нарис.27показанарасчетнаясхемабалки,нагруженнойраспреде-

ленной нагрузкой q = 2ρc и изгибающими моментами M0

на концах.

Теория упругости. Часть II

Рис. 27

Решение в элементарной теории изгиба, как и в предыдущей задаче, имеет следующий вид:

σx =	M	z y; σy = 0; τxy =	QS отс		(4.63)
			z	,
	I z		I z

где поперечная сила и изгибающий момент определяются соответственно по формулам

	Q = −2ρcL + 2ρc(L − x) = −2ρcx;								(4.64)
	M z = M0 + 2ρcL(L − x)−2ρc 1 (L − x)2						=
			2
= M0	+ 2ρc(L − x)[L − 1 (L − x)]= M0 +ρc(L2						− x2 );		(4.65)
	2
	статическиймоментотсеченнойчастисечения,
	расположеннойнижеуровня y ,равен(рис.28)
		отс				c − y		=
	Sz		=1 (c − y) c −				2	=
							2
	=1	(c − y)(c + y)		=	(c2 − y2 )			.	(4.66)
	=1		2	=			2	.	(4.66)
			2				2
Рис. 28	Выражения для напряжений (4.63) с уче-
Рис. 28	том (4.64)–(4.66) примут окончательный вид

Задача 4. Плоская задача теории упругости. Функция напряжений

σx =	M y =		M0 +ρc (L2 − x2 ) y;
	Iz			Iz
σy	= 0;	τxy = −		ρc(c	2	− y	2	).	(4.67)
σy	= 0;	τxy = −		ρc(c		− y		).
					Iz

4.5.4.Анализ полученных решений

1.Формулы для касательных напряжений τxy , полученные в теории упругости и элементарной теории изгиба, совпали.

2.Выражение для напряжения σx из соотношений (4.62) можно

представить в виде суммы двух слагаемых:

• первое (основное) слагаемое

осн	=	M 0	y +	ρc	2	− x	2	)y	(4.68)
σx		I z		I z	(L

совпадает с решением элементарной теории изгиба (4.67);

• второе (дополнительное) слагаемое

доп		ρ		3		3		2
σx	=		y		−		c		y
σx	=	c2	y		−	5	c		y
		c2				5

представляет необходимую поправку, учитывающую надавливание продольных волокон друг на друга.

Если на торцах изгибающая нагрузка распределена по линейному закону, то выражение напряжения σx (4.68) является точным ре-

шением задачи.

Дополнительноеслагаемое независитоткоординатыx(см.рис.26) и при значении y = c имеет следующее значение:

доп

σx

−

= 0,4ρc.

y =c

Второе слагаемое в выражении для напряжения σx (4.62) имеет следующее значение:

осн		ρc	2		2		54ρc	при x = 8c; y = c;
осн		ρc	2		2		54ρc	при x = 8c; y = c;
σx	=		(L	− x		)y	=	при x = 0; y = c.
		I z					L =10c 150ρc	при x = 0; y = c.
		I z					L =10c 150ρc

Теория упругости. Часть II

Поправка к величине σоснx в виде σдопx в середине пролета балки (при x = 0) составляет 0,27 %, а на расстоянии, равном высоте балки

от торца (при x = 8c

Рис. 29

), – 0,74 %. Следовательно, действием поверхно-

стныхсамоуравновешенныхнагрузок на торцах, параллельныхоси x, на напряженное состояние на расстоянии от торца, равном высоте сечения, можно пренебречь.

3. В элементарной теории изгиба используется гипотеза об отсутствии давления продольных волокондруг надруга. Всвязисэтим принимается, что напряжения

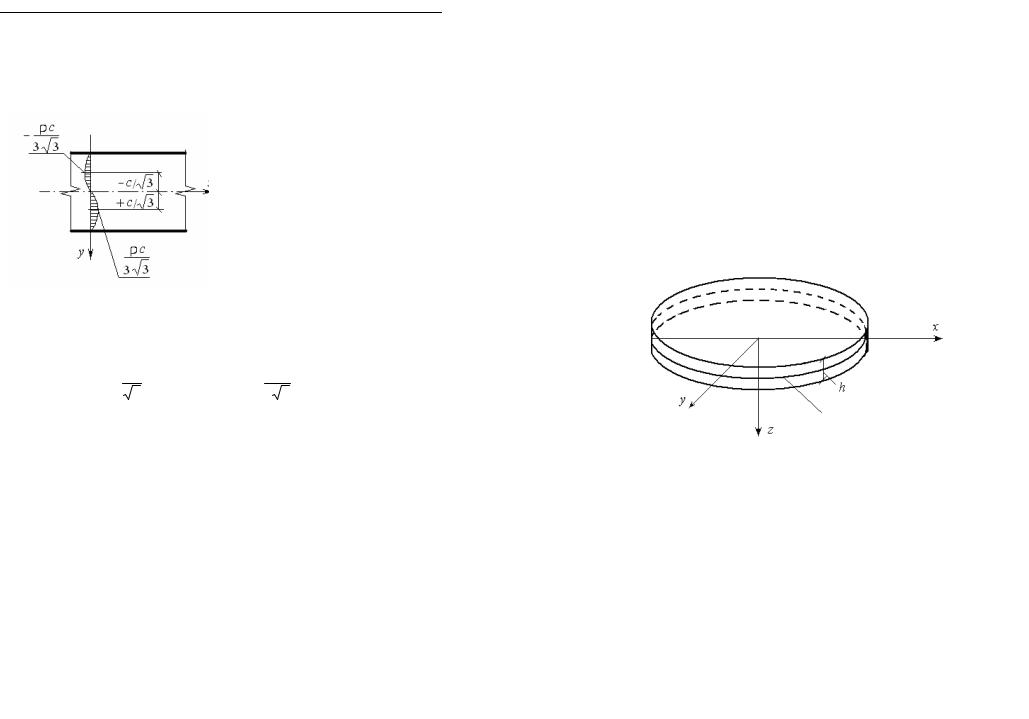
σy = 0. Однаков теории упругости давление волокон друг на друга

учитывается в виде напряжения σy . Изменение по высоте сечения этого напряжения показано на рис. 29. Его наибольшее значение воз-

никает в точке y = c3 и равно (σy )max = 3ρc3 .

Задача 5. РАСЧЕТ ТОНКИХ ПЛИТ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ

5.1. Введение

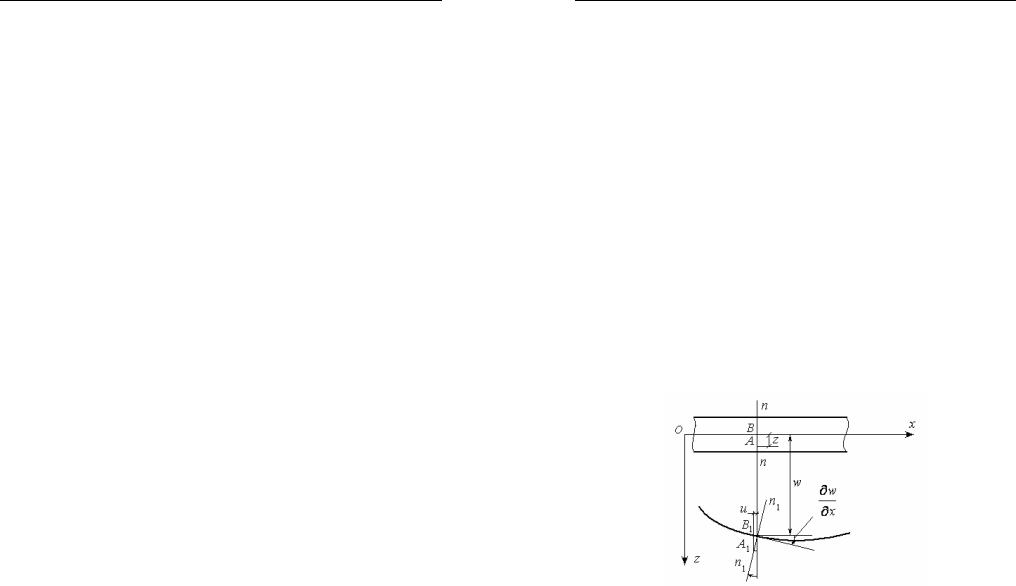
Тело, у которого толщина мала по сравнению с другими размерами, называется тонкой плитой или пластинкой. Рассмотрим плиту, которая имеет постоянную толщинуh (рис. 30). Плоскость, равноотстоящая от верхней и нижней поверхностей плиты (делящая толщину плиты пополам), называется срединной плоскостью плиты.

Срединная плоскость

Рис. 30

Оси x и y лежат в срединной плоскости недеформированной плиты.

Для большинстваинженерных конструкций точноерешение системы основных уравнений, которые получены в теории упругости, оказываетсяоченьтрудным, а частоиневозможным. Втакихслучаях приходится применять или приближенное решение системы уравнений, или принимать некоторые упрощения, более или менее справедливыелишьдляопределенноготипаконструкций(тонкостенныхстержней, тонких плит, оболочек и т. д.). Решение задачи определения напряженийидеформаций,полученноетакимобразом,являетсяприближенным. Однако опыты с конструкциями, для которых получены

Теория упругости. Часть II

приближенные решения, указывают, что эти решения часто оказываются вполне приемлемыми для инженерной практики.

Будем рассматривать малые деформации тонких плит под действием нагрузок, перпендикулярных срединной плоскости.

Под малыми деформациями подразумеваются такие деформации, при которых прогибы удовлетворяют соотношению

w <	1 h.	(5.1)
Плиты называются тонкими,	3
Плиты называются тонкими,	если их толщины удовлетворяют
соотношению
h < 1 Lmin ,		(5.2)
5

где Lmin – наименьший размер плиты в плане.

Решениярассматриваемойнижеприкладнойтеориитонкихплит в оговоренном диапазоне плит и величин деформаций имеют удовлетворительную для технических расчетов точность. Они получены на основании следующих двух допущений, предложенных Кирхгофом:

1.«Гипотеза прямых нормалей». Нормали к срединной плоскости до нагружения после изгиба в результате деформации не искривляются и остаются перпендикулярными срединной поверхности.

Это допущение аналогично «гипотезе плоских сечений» в теорииизгибабалок.Онопредставляет,посуществу,пренебрежениевлиянием деформации сдвига на общее напряженно-деформированное состояние плит. Так же каки для балок, указанное допущение вносит тем бóльшую погрешность, чем толще плита по сравнению с ее пролетами.

2.Напряжения σz поплощадкам,параллельнымсрединнойплос-

кости плиты, малы по сравнению с другими компонентами напряжения, т. е.

σz << σx ; σz << σy.

(5.3)

Это допущение аналогично допущению теории изгиба балок о том, что «продольные волокна не давят друг на друга». Оно может внести ощутимую погрешность только для весьма толстых плит.

На основании допущения (5.3) в формулах обобщенного закона Гука (3.4) можно отбросить σz как величину весьма малую по срав-

Задача 5. Расчет тонких плит при поперечном изгибе

нению с расположенными рядом напряжениями σx и σy . Исходя из этого имеем

εx	=	1	[σx −µσy ];
εx	=	E	[σx −µσy ];		(5.4)
		E
εy	=	1	[σy −µσx ].
		1
		E
		E
Откуда следует, что
σx =		E		[εx +µεy ];
σx =	1 −µ2			[εx +µεy ];
	1 −µ2
σy =		E		[εy +µεx ].	(5.5)
σy =	1 −µ2			[εy +µεx ].
	1 −µ2

5.2. Выражения напряжений через прогибы срединной поверхности плиты

На рис. 31 представлена проекция на плоскость xOy перемещения произвольной точки плиты A.

Рис. 31

Эта точка находилась до деформации на нормали n n , проходящей через точку B (x, y ) срединной плоскости плиты, и располага-

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.09.2019608.16 Кб9svetotekhnika.docx
#
26.08.2019650.27 Кб3SX Meagher - All That Matters.docx
#
23.09.2019346.62 Кб9TEA-3_Otvety_k_ekzamenu.doc
#
29.03.20152.85 Mб40temy_po_organizatsii_stroitelstva.docx
#
29.03.2015649.42 Кб88Teoria_uprugosti_Ch1_Ledovskoy_12.pdf
#
29.03.2015650.8 Кб219Teoria_uprugosti_Ch2_Ledovskoy_12.pdf
#
29.03.20154.19 Mб37teor_stat[1].pdf
#
29.03.201536.56 Кб8text primer.docx
#
29.03.201580.02 Кб19text_raboty (1).docx
#
08.09.2019308.3 Кб4The Provincetown Tales 3 - Distant Shores, Sile...docx
#
29.03.2015208.17 Кб31Tihonov_i_dr_uchebn.pdf