Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет — учебно-научно-производственный комплекс (бывш. ОрелГТУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Burlakova_Matematika_ryadi

.pdf

Скачиваний:

Добавлен:

28.03.2015

Размер:

523.82 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Решение:

а) так как cos10 cos , то в разложение функции

cosx 1

... ( 1)n

x2n

...,

(2n)!

где x , подставим x

... или cos10 1 0,1745 2

0,1745 4

cos

...

Так как полученный ряд является знакочередующимся рядом

Лейбница и

0,1745 4

(0,2)4

0,0016

0,0001, то требуемая точность

будет обеспечена, если ограничиться только первыми двумя членами полученного разложения.

Итак, cos10 1 0,1745 2 0,9848; 2!

б) 4630 4625 5 4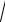625(1 0,008) 541 0,008 5(1 0,008)4 .

Используем биномиальный ряд

(1 x)m 1 m x m(m 1) x2 ... m(m 1)...(m n 1) xn ..., где 1 x 1. 1! 2! n!

Полагая x 0,008					и m		1	, получим следующее разложение:

						4
1			1			3		(0,008)2	3 7	(0,008)3 ...
(1 0,008)	4	1		0,008
						16 2!			64 3!
		4
		1

или (1 0,008)4 1 0,002 0,000006 0,000000028 ... .

Если в последнем знакочередующемся ряде учитывать только первые два члена, а остальные отбросить, то погрешность при вычислении 41 0,008 не превысит по абсолютной величине 0,000006. Тогда погрешность при вычислении 4630 541 0,008 не превысит числа

5 0,000006 0,00003 0,0001. Следовательно,

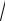4630 541 0,008 5(1 0,002) 5,0100.

Пример 3. Вычислить интегралы с точностью до 0,001:

2 dx

а) 0 31 x2

Решение:

2 dx

а) 0 31 x2

		1
	2		sin2x
;	б)		sin2x	dx.
;	б)			dx.
	0		x
	0

(1 x2) 3 dx.

Разложим подынтегральную функцию в степенной ряд. Для этого

подставим в биномиальный ряд m 1 и заменим x на x2:

(1 x2)	1		1	x2		2	x4			14		x6 ... .
	3	1

		3			9				81
Так как отрезок интегрирования								0;			1		принадлежит области

											2

сходимости полученного ряда ( 1;1), то будем интегрировать почленно в указанных пределах:

1						1											x3	2x5	14x7	1
2			dx			2		1			2		14
2			dx			2		1		x2	2	x4	14	x6							2
							1								... dx	x				...


0	3 1 x2				0			3			9		81				9	45	567
0	3 1 x2				0			3			9		81				9	45	567	0
		1		1		1			7		... .
					720			36288			... .
	2		72		720			36288

В полученном знакочередующемся ряде четвертый член по абсолютной величине меньше 0,001. Следовательно, требуемая точность будет обеспечена, если учитывать только первые три члена ряда.

1
2			dx		1	1	1		39	0,4875.
0										0,4875.
0	3	1 x2		2		72	720	80

Так как первый из отброшенных членов имеет знак минус, то полученное приближенное значение будет с избытком. Поэтому данный интеграл с точностью до 0,001 равен 0,487;

б) предварительно представим подынтегральную функцию в виде степенного ряда. Заменим в разложении функции

sinx x	x3		x5		x7	... ( 1)n 1	x2n 1	..., где	x ,
							(2n 1)!
3!		5!		7!
						31

x на 2x, получим:

sin2x 2x								(2x)3										(2x)				5				(2x)7					...
sin2x 2x										3!																	7!				...
										3!						5!							23 x2				7!			25 x4					27 x6
	Тогда								sin2x								2						23 x2							25 x4					27 x6		... .
	Тогда																2																				... .
1							1				x													3!							5!		7!
1							1
2 sin2x							2							23 x2									25 x4							27 x6
		dx								2

	x															3!								5!							7!	... dx
0	x						0									3!								5!					1		7!
		2		3	x	3				2		5	x		5				2		7	x		7					1					1			1	1
	2x			3		3						5			5						7			7					2										... .
																									...						1
																									...						1
			3!3								5!5									7!7													18			600		35280
			3!3								5!5									7!7								0					18			600		35280

Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Четвертый член ряда по абсолютной величине меньше 0,001. Чтобы обеспечить требуемую точность, достаточно найти сумму первых трех членов.

	1
2		sin2x			1	1
Следовательно,			dx 1				0,946.
				18		600
0		x

Пример 4. Найти пять первых членов разложения в степенной ряд решения дифференциального уравнения:

а)

y x2

y2 , если

y(1) 1;

б)

, если

y(1) 1 и

y (1) 0.

Решение:

а) при решении задачи Коши

y f (x;y),

y(x0) y0

используется ряд Тейлора

(n)

(x0)

y(x)

(x x0)n ,

n 0

где y0 y(x0), y (x0) f (x0;y0), а остальные производные находятся путем последовательного дифференцирования исходного уравнения и подстановки начальных данных в выражения для этих производ-

ных.						y (1) 1 1 2. Дифференци-
Из данного уравнения находим, что						y (1) 1 1 2. Дифференци-

руем исходное уравнение:
y	2x
y	2x		2yy ,	y (1) 2 2 2 6;
y			2		y
y		2 2(y )		2yy ,	y	(1) 22;
				32

y	(4)					2yy		y	(4)	(1) 116
y		4y y		2y y		2yy	,	y		(1) 116

и т.д.

Подставляя найденные значения производных в ряд, получаем:

y(x) 1 2(x 1)

6(x 1)2

22(x 1)3

116(x 1)

...

1 2(x 1) 3(x 1)2

11(x 1)3

29(x 1)4

...;

(n)

(1)

б) ищем решение в виде ряда y(x)

(x 1)n .

n 0

Из уравнения и начальных условий имеем, что y (1) 1.

Дифференцируя уравнение, получим:
			y				1		y		2	2		x	2		,						0;
			y		y y				y			(y )		x			,	y		(1)			0;
y	(4)			1					2	y	2y		3		3	2x			3		,	y	(4)	(1) 2.
y		y y				3y y				y	2y			(y )		2x					,	y		(1) 2.
Таким образом, искомое решение примет вид
y(x) 1			(x 1)2					2(x 1)4				... 1			(x 1)2							(x 1)4			... .
y(x) 1												... 1													... .
		2				24												2					12

Пример 5. Проинтегрировать уравнение y 2y x. Решение: будем искать решение в виде степенного ряда

y a0 a1x a2x2 ... anxn ....

Отсюда					y a1		2a2x ... nanxn 1 ... . Подставляя																					y и		y в исход-
ное уравнение, получим:																										xn ...) x .
a	2a	2	x ... na xn 1						... 2(a					0	a x a				2		x	2 ... a			n	xn ...) x .
1		2					n							0	1				2						n
Приравниваем коэффициенты при одинаковых степенях x:
													x0			a	2a			0		0,
															1					0
												x1				2a	2	2a				1,
																	2				1
												x2				3a3 2a2 0,
												x3				4a4 2a3 0,
											…………………. .
Из решения этой системы получим:
							1								2 1									1 2			1
a	2a			,	a			2a		,	a						2a				, a							2a		,....
a	2a			,	a		2	2a		,	a						2a				, a			2 3				2a		,....
1			0			2	2		0			3			3 2				0				4	2 3			2		0
															33

Подставляя в решение неопределенные коэффициенты, выраженные через a0 , будем иметь


y a	0	2a		0	x 2a				0	x2			2		2a			0	x3		2	2	2a		0	x4			2	2 2	2a		0	x5	...			1	x2			1	2	x3
y a		2a			x 2a					x2					2a				x3				2a			x4					2a			x5	...				x2					x3
										3										4 3								5 4 3									2			2 3
			1			2	2				1	2		2		2								( 1)			n	a0		(2x)		n			( 1)	n	(2x)			n
			1			2	2	x4			1	2		2		2	x5 ...							( 1)				a0		(2x)					( 1)		(2x)				.
								x4									x5 ...											n!							4n!						.
		2 3 4								2 5 4 3												n 0						n!						n 2	4n!

Неопределенный коэффициент a0 играет роль произвольной постоянной интегрирования. Пользуясь признаком Даламбера, нетрудно доказать, что полученные ряды сходятся на всей числовой оси.

Задания для самостоятельной работы

1. Найти области сходимости функциональных рядов:

1)n 1 n!(x 3)n ;

4) sinnx ;

n 1 enx

7) n e nx ;

n 1

2)n 1 (x 5)n ;

5) lnn x ;

n 1 n

8) e n2x .

n 1

3) cosnx ;

n 1 n n

x 1 n

6) ;

n 1 x 1

2. Исследовать на равномерную сходимость функциональные ряды:

sinnx

cosnx

( ; );

n 1

1;1 .

n 1 n

3. Найти области сходимости степенных рядов:

;

2) ( 1)n

;

3) 2n 1 x2n 2 ;

n 1

n 1 n 10

n 1

;

n 1

n 1 n(n 1)

n 1 3 2

n 1 (2n 1) 3n 1

2n 1

xn ;

8) 5n2

xn2 ;

( 1)

;

2n 1

n 1

2n 1

n 1

(nx)

( 1)

n 1

(3x

10)

;

11)

(x 3)

;

12)

;

n 1

(2n 1)!

n 1

n 5

n 1

1)2

(2x 1)

13)

;

14) (x 1)n tg

3n 2

n 1

4. Разложить в ряды Маклорена функции:

										2)		f (x) cos( 3x);
1)	f (x) x 16 2x ;									2)		f (x) cos( 3x);							3)	f (x) sin(x2);
4)	f (x) e x2 ;									5)		f (x) cos2 x;							6)	f (x)					1 x		;
7)	f (x)				7				;	8)		f (x)		1			;		9)	f (x) ex ln(1 x);
7)	f (x)			10 3x x2					;	8)		f (x)					;		9)	f (x) ex ln(1 x);
				10 3x x2									1 x2
10) f (x)							cosx	.		11)		f (x) sin2 4x							12)		f (x) ln(1 3x 10x2 ).
10) f (x)							1 x	.
							1 x
5. Вычислить выражения с заданной точностью:
1)	e2 с точностью до 0,001;												2)		1			с точностью до 0,0001;
													2)		e			с точностью до 0,0001;
															e
3)	cos18 с точностью до 0,001;													4) sin12					с точностью до 0,00001;
5)						с точностью до 0,001;							6) 3						с точностью до 0,0001;
5)		1008				с точностью до 0,001;							6) 3			130			с точностью до 0,0001;
7)	ln3 с точностью до 0,0001;													8) ln1,3					с точностью до 0,001;
9)	arctg		1			с точностью
9)	arctg					с точностью
	5
до 0,0001.
6. Вычислить интегралы с точностью до 0,001:
	1										1									1
										2
										2
1)	cos			xdx;				2)		1 x3dx;									3) 3				x	cosxdx;
	0									0										0
	1										1										1
	1									2										2		arctgx
4)	sin(x2)dx;							3)		xln(1 x2)dx;									6)			arctgx				dx.
4)	sin(x2)dx;							3)		xln(1 x2)dx;									6)							dx.
	0									0										0			x
	0									0										0

7. Найти суммы функциональных рядов и указать области их сходимости к этим суммам:

n 2

;

(n 1)x2n

n 1

n 1n(n 1)

n 0

( 1)

n 1

4) n2n xn ;

;

6) (2n2 2n 1)xn .

3n 1

n 1

8. Проинтегрировать уравнения:

y x,

y(0) 0, y (0) 0;

y x y2 1,

y(1) 2.

9. Записать первые пять членов разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего заданным начальным условиям:

y ey xy,

y(0) 0;

y 1 x x2

2y2, y(1)

;

x y

y y ,

y(0) 1, y (0) 0

y(0) 0, y (0) 1.

3. РЯДЫ ФУРЬЕ

Контрольные вопросы для самопроверки

1.Какой ряд называется тригонометрическим рядом?

2.Сформулируйте определение тригонометрического ряда Фурье

спериодом 2 .

3.Сформулируйте теорему Дирихле о достаточных условиях разложения в ряд Фурье периодической функции с периодом 2 .

4. Запишите ряд Фурье для функции f (x), четной на отрезке

; ; нечетной на отрезке ; .

5.Как определяются коэффициенты Фурье для периодической функции f (x) с периодом 2l? Какой вид принимает ряд Фурье для

такой функции?

6. Запишите ряд Фурье для функции f (x), четной на отрезкеl;l ; нечетной на отрезке l;l .

Примеры решения задач

Пример 1. Разложить в ряд Фурье функцию с периодом 2 :

			2,		x 0,
			f (x)	3,	0 x .
				3,	0 x .
Решение: изобразим график данной функции на отрезке ;
и ее периодическое продолжение на всю числовую ось:
				y
				3
-4	-3	-2		0		2	3	4 x
					-2

Заданная функция удовлетворяет условиям теоремы о разложимости в ряд Фурье, так как на отрезке ; функция имеет одну точку разрыва первого рода ( при x 0), а во всех других точках этого отрезка она непрерывна. Следовательно, справедливо равенство:

						a0
					f (x)	a0	(an cosnx bn sinnx).
					f (x)		(an cosnx bn sinnx).
					2		n 1
	Подсчитаем коэффициенты Фурье:
	1		1	0				1	0			1
a0		f (x)dx			2dx 3dx					2x	2x 0		1;


					0
					0
									37

			1												1			0
																				2cosnxdx 3cosnxdx
an					f (x)cosnxdx															2cosnxdx 3cosnxdx
																												0
																												0
	1		2sinnx 0									3sinnx
																							0;
																							0;
					n											n
					n											n					0
			1												1		0
																				2sinnxdx 3sinnxdx
bn					f (x)sinnxdx															2sinnxdx 3sinnxdx
																											0
																											0
	1		2cosnx					0			3cosnx														1
																										(2 2cos( n) 3cos n 3)
																										(2 2cos( n) 3cos n 3)
					n											n								n
					n											n								n
																						0
	5									5									2 n				10
			(1 cos n)									2sin													,	n нечетное,
																									,	n нечетное,
																							n
									n											2			n
	n								n											2				0,		n четное.
																								0,		n четное.
		Подставив найденные коэффициенты, получим следующее раз-
ложение данной функции в ряд Фурье:
				1		10							1									1					1
f (x)							sinx							sin3x									sin5x					sin7x ... .
f (x)				2			sinx						3	sin3x								5	sin5x				7	sin7x ... .
				2									3									5					7
		Полученное равенство справедливо при любом значении x, ис-
ключая						точки					разрыва											x n					(n 1, 2...),		где сумма ряда равна

2 3 1 , то есть равна среднему арифметическому значению дан-

2 2

ной функции слева и справа от точки разрыва.

Пример 2. Разложить в ряд Фурье функцию с периодом 2 :

f (x) x.

Решение: изобразим график данной функции на промежутке; и ее периодическое продолжение на всю числовую ось:

−4

−2

−

Так как данная функция является нечетной, то коэффициенты an 0. Находим коэффициенты bn :

					sinnx						2	,			n нечетное,
	2		2	xcosnx				2
	2		2	xcosnx				2
bn		f (x)sinnxdx								cosnx n
bn		f (x)sinnxdx				2				cosnx n
		0		n	n		0		n				2	,	n четное.
		0		n	n		0		n					,	n четное.
													n
					38

Следовательно, разложение данной функции в ряд Фурье имеет вид:

	1		1		1
f (x) 2 sinx		sin2x		sin3x		sin4x ... .
f (x) 2 sinx	2	sin2x	3	sin3x	4	sin4x ... .
	2		3		4
Пример 3. Разложить	в ряд Фурье функцию с периодом 2

f (x) x2 , x ; .

Решение: изобразим график данной функции на промежутке; и ее периодическое продолжение на всю числовую ось.

−4

−2

Данная функция является четной, следовательно, коэффициенты bn 0. Определим a0 :

	2		2		2 x3			2	2	.
a0		f (x)dx		x2dx
						3		3
		0		0			0

Для вычисления коэффициентов an дважды применим интегрирование по частям:

2 sinnx

cosnx

2sinnx

f (x)cosnxdx

cosnxdx

n нечетное,

cos n

n четное.

Следовательно,

f (x) x2 2

	cos2x	cos3x
4 cosx			... .
4 cosx	22	32	... .
	22	32

Полученное равенство справедливо при любом x. В частности, при x 0, получаем:

	2		1	1	1		,
0		4 1				...
	3		22	32	42

то есть	2	1	1		1		1	... ,	S	2	.
12			22	32		42			12
									39

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.20151.89 Mб26Bobylev_kulturarechi_2001.pdf
#
28.03.20151.13 Mб153bobylev_kyltura_rechi_1.pdf
#
28.03.20151.41 Mб19Bobylev_prakt_po_ritor.pdf
#
12.03.20162.41 Mб46Bodrov.rtf
#
15.12.2018195.5 Кб6BO_vse_temy.docx
#
28.03.2015523.82 Кб10Burlakova_Matematika_ryadi.pdf
#
24.09.2019158.72 Кб3BZhD_1.doc
#
28.03.2015506.88 Кб60Chernova_statistika_1.doc
#
11.11.2019639.49 Кб8Chernova_statistika_2.doc
#
09.11.201965.39 Кб4Chistovik.docx
#
28.03.20151.83 Mб12chistyakov.doc