
Burlakova_Matematika_ryadi
.pdf
ж) общий |
член |
данного ряда |
an |
|
1 |
эквивалентен при |
||||||||
ln 1 |
|
|
||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
n дроби |
|
. Сравним данный ряд со сходящимся рядом |
|
|
||||||||||
|
2 |
2 |
|
|||||||||||
|
n |
|
1 |
|
|
|
|
|
|
n 1 |
n |
|||
при p 2 1 , тогда b |
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n |
|
n2 |
|
|
|
|
|
|
|
|
|
Применим второй признак сравнения. Так как
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
an |
|
|
|
ln 1 |
n2 |
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
|
lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
lim |
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
|
|
|
ln 1 |
|
|
1 |
n2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
n bn |
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
n2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
lim |
|
|
|
|
ln e 1 0, |
|
то исследуемый ряд также сходится; |
|||||||||||||||||||||||||||||||||||||||||||
ln |
1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n3 2 |
|
|
|
|
n3 2 |
|
|
|
|
|
|
|
|
||||||||
|
и) так как для любого n |
|
sinn |
|
1, то |
|
|
|
|
|
|
|
|
|
n2 |
1 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
n |
2 |
sin |
2 |
n |
|
|
n |
2 |
|
|
n |
2 |
1/2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
для n 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Сравним исходный ряд с |
|
1 |
|
– обобщенным гармоническим |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1/2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
рядом, который также называют рядом Дирихле; он расходится, так как 1 1.
2 |
|
|
|
|
|
|
|
|
|
|
Возвращаясь к соотношению |
|
|
n3 2 |
|
|
1 |
, по первому признаку |
|||
n |
2 |
sin |
2 |
n |
1/2 |
|||||
|
|
|
|
|
n |
|
||||
сравнения заключаем: данный ряд расходится.
Пример 2. Исследовать на сходимость ряды с помощью признака Даламбера:
|
2 |
|
|
n |
|
|
2 |
|
|
а) |
n |
; |
б) |
; |
в) |
2 |
1 |
. |
|
2n 1 |
|
n |
|
||||||
n 1 |
3 |
|
n 1 |
n! |
n 1 |
3 1 |
|||
Решение:
а) так в общем члене данного ряда содержится показательная функция, то применим признак Даламбера.
Имеем an |
|
n2 |
, an 1 |
|
(n 1)2 |
|
(n 1)2 |
. |
32n 1 |
32(n 1) 1 |
|
||||||
|
|
|
|
|
32n 1 |
|||
|
|
|
|
|
|
10 |
|
|

l lim |
a |
n 1 |
|
(n 1)2 32n 1 |
|
(n 1)2 |
~ n2 |
|
n2 |
32n 1 |
1 |
|
|
|
lim |
|
|
|
|
lim |
|
|
|
|
. |
||
|
|
32n 1 n2 |
n |
|
|
|
|||||||
n an |
n |
|
n 9 32n 1 n2 |
9 |
|
||||||||
Так как l 1 1, то по признаку Даламбера данный ряд сходится;
9
б) так в общем члене данного ряда содержится факториал, то применим признак Даламбера.
Имеем an |
|
nn |
, |
an 1 |
(n 1)n 1 |
. |
|
|
|
|
|
|
|
||||||||
n! |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
(n 1)! |
|
|
|
|
|
|
|
||||
l lim |
|
a |
n 1 |
|
|
|
(n 1)n 1 n! |
|
|
(n 1)n (n 1) n! |
n 1 |
n |
|
||||||||
|
|
lim |
|
|
|
lim |
|
|
lim |
|
|
|
|
||||||||
|
|
|
|
|
|
n!(n 1) nn |
n |
||||||||||||||
|
n an |
n (n 1)!nn |
n |
n |
|
|
|||||||||||||||
|
|
1 |
|
n |
e. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как l e 1, то по признаку Даламбера исследуемый ряд расходится;
в) так в общем члене данного ряда содержится показательная функция, то применим признак Даламбера.
Имеем an |
2n 1 |
, |
an 1 |
2n 1 |
1 |
. Тогда |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
3n 1 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3n 1 |
|
|
|
1 |
|
|
|
|
|
||||||||||||
l lim |
|
an 1 |
|
lim |
|
2n 1 1 |
|
3n 1 |
lim |
3n 1 |
|
2n 2 1 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
n an |
|
n 3n 1 1 2n 1 |
|
n 3n 3 1 |
|
2n 1 |
|||||||||||||||||||||||||||
|
1 |
|
1 |
|
|
|
2 |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
lim |
3n |
|
|
|
|
|
2n |
|
|
. Так как l |
1, то по признаку Даламбера ис- |
||||||||||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||
n |
3 |
|
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||||||
|
3n |
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
следуемый ряд сходится.
Пример 3. Исследовать на сходимость следующие ряды с помощью радикального признака Коши:
|
|
n 1 |
|
|
|
|
|
3n2 5 n |
|
|
|
|
|
n 1 n2 |
||||||||
а) arctg |
|
|
; |
|
|
б) |
|
|
|
|
|
|
; |
|
|
|
|
в) |
|
. |
||
|
|
|
2 |
|
|
|
||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
n 1 2n 7 |
|
|
|
|
|
n 1 |
n |
|||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а) an |
arctgn |
1 |
, |
l limn |
|
limn arctgn |
1 |
|
limarctg |
1 |
0. |
|
|
|||||||||
an |
|
|
||||||||||||||||||||
|
|
n |
|
|
||||||||||||||||||
|
|
|
|
|
n |
n |
n |
|
|
|
|
n n |
|
|
|
|||||||
Так как l 0 1, |
то по радикальному признаку Коши ряд расхо- |
|||||||||||||||||||||
дится; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 n |
|
|
|
|
|||
б) запишем общий член ряда an |
|
3n2 |
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
7 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n2 5~ 3n2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
3n2 |
5 |
n |
|
3n2 5 |
|
3n2 |
3 |
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l lim |
|
an |
lim |
|
|
2n |
2 |
7 |
|
lim |
2 |
7 |
|
2n |
|
7 ~ 2n |
|
lim |
|
2 |
. |
|||
n |
|
|
n |
|
|
|
|
n 2n |
|
|
|
n |
|
n 2n |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как l 3 1, то по радикальному признаку Коши данный ряд
2
расходится;
n 1 n2
в) запишем общий член ряда an .
n
|
|
|
n 1 |
n2 |
n 1 |
|
|
1 n |
e. |
|||||
l lim n an |
|
|||||||||||||
lim n |
|
|
|
lim |
|
|
|
lim 1 |
|
|
||||
n |
n |
|
||||||||||||
n |
n |
|
|
n |
|
n |
n |
|
||||||
Так как ряд l e 1, то по радикальному признаку Коши данный ряд расходится.
Пример 4. Исследовать на сходимость следующие ряды с помощью интегрального признака сходимости:
|
1 |
|
|
|
|
1 |
|
|
|
|
а) |
|
; |
|
б) |
; |
|
||||
1 n |
2 |
|
||||||||
n 1 |
|
|
|
n 1 |
3n 1 |
|
|
|||
|
1 |
|
|
|
|
1 |
|
|
|
|
в) |
|
; |
г) |
|
|
|
. |
|||
|
|
|
|
|||||||
|
|
|
|
2 |
|
|||||
n 1 |
n(n 3) |
n 2 |
n ln |
n |
||||||
|
|
|
|
|
|
|
||||
Решение:
а) применим интегральный признак Коши.
Чтобы составить функцию f (x), достаточно в формуле общего
члена ряда заменить n на х. Таким образом, f (x) |
1 |
. Как видно, |
|
||
1 x2 |
|
|
функция на промежутке 1; ) является непрерывной, положительной и убывающей. Рассмотрим соответствующий несобственный интеграл:
|
dx |
2 |
b |
dx |
2 |
lim arctg x |
|
1 |
lim arctgb arctg1 |
. |
|
|
lim |
|
|||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
1 1 x |
|
n 1 1 x |
|
n |
|
|
n |
4 |
|
||
|
|
|
|
||||||||
Так как несобственный интеграл сходится, то по интегральному признаку Коши сходится и исследуемый ряд;
12
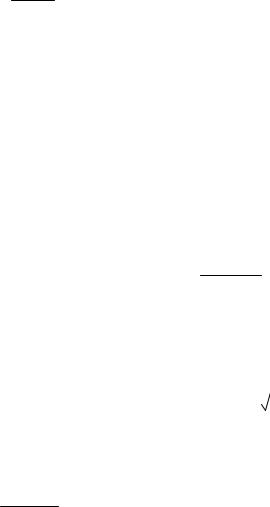
б) для данного ряда f (x) 1 . Очевидно, что функция f (x) на
3x 1
промежутке 1; ) является непрерывной, положительной и убывающей. Рассмотрим несобственный интеграл:
|
dx |
|
|
b |
|
1limln(3x 1) |
|
1lim ln 3b 1 ln 4 . |
|||||
|
|
|
|
||||||||||
|
1lim d(3õ 1) |
b |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3õ 1 |
|
|
3b 1 |
3õ 1 |
|
3b |
1 |
|
3b |
|||
|
|
|
|
||||||||||
Так как несобственный интеграл расходится, то по интегральному признаку Коши исследуемый ряд расходится;
в) для данного ряда f (x) |
1 |
. Функция на промежутке 1; ) |
|
||
|
x(x 3) |
|
непрерывна, положительна и убывает.
Разложим правильную рациональную дробь
1
на сумму
x(x 3)
простейших дробей: |
1 |
|
A |
|
B |
. Получим |
A |
1 |
, B |
1 |
. |
|
x(x 3) |
|
x x 3 |
3 |
3 |
||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
1
dx |
|
1 |
|
b |
|
1 |
|
1 |
1 |
|
b |
|
b |
|
1 |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
ln4 ln3 4. |
||||||||||||||||
|
|
|
lim |
|
|
|
|
|
dx |
|
lim |
ln |
|
|
ln |
|
|
|
|
|||||
x(x 3) |
|
|
x 3 |
|
b 3 |
4 |
3 |
|||||||||||||||||
|
3b |
1 |
x |
|
|
3b |
1 |
|
|
|
|
|
|
|
||||||||||
Так как несобственный интеграл сходится, то по интегральному признаку Коши сходится и исследуемый ряд;
г) для данного ряда f (x) 1 .
x ln2 x
Функция на промежутке 2; ) непрерывная, положительная, убывающая.
Рассмотрим несобственный интеграл
dx |
|
b dlnx |
|
1 |
|
b |
|
1 |
|
1 |
|
|
1 |
. |
||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
lim |
|
|
|
lim |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||||||||
2 |
xln |
|
x |
b 1 |
ln |
|
x |
b lnx |
|
2 |
b lnb |
|
ln2 |
|
|
ln2 |
|
|||
|
|
|
|
|
|
|||||||||||||||
Данный интеграл сходится. Следовательно, и данный ряд сходится по интегральному признаку Коши.
1.3.Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость
Примеры решения задач
Пример 1. Исследовать следующие ряды на сходимость:
|
1 |
|
|
|
n |
|
а) ( 1)n 1 |
|
; |
б) |
( 1) |
|
; |
n |
|
|||||
|
|
|||||
n 1 |
|
n 2 |
lnn |
|||
|
|
|
13 |
|
|
|

|
|
n 1 |
2n 1 |
|
|
1 |
|
|
|
|
|
|
|
|
|||
в) |
( 1) |
; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
г) ( 1)n 1 |
|
|
|
; |
|
|
|
|
|
|
|||
|
|
|
3n 2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
n 7 |
n |
|
|
|
|
|
|||||||
|
n 1 |
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|||
|
|
|
n 2 ( 1)n |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
д) ( 1) |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
n 1 1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
а) исследуем ряд из абсолютных величин |
( 1) |
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n 1 |
|
|
|
|
n |
|
|
n 1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Получившийся ряд является гармоническим и он расходится. Проверим условие признака Лейбница. Данный знакочередующийся ряд удовлетворяет условиям признака Лейбница. Члены ряда по абсолютной величине монотонно убывают, так как
1) 1 |
1 |
|
1 |
|
1 |
... |
1 |
... ; |
|
|
|
n |
|||||
2 |
3 |
4 |
|
|
||||
2) 2) lim an lim 1 0.
n
Следовательно, по признаку Лейбница ряд сходится. А так как ряд из абсолютных величин расходится, то исследуемый ряд
|
|
n 1 |
1 |
сходится условно; |
|
|
|
|
|
|
|
||
|
( 1) |
|
|
|
|
|
|
|
|||||
|
n |
|
|
|
|
|
|
|
|||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1) |
n |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
б) исследуем ряд из абсолютных величин |
|
|
|
|
|
|
. |
|||||
|
lnn |
|
|||||||||||
|
|
|
|
n 2 |
|
|
|
|
n 2lnn |
||||
Этот ряд был исследован в примере 1, в) пункта 1.2 и он там расходился, следовательно, проверим теорему Лейбница.
Данный знакочередующийся ряд удовлетворяет условиям признака Лейбница:
1) |
1 |
|
|
|
1 |
|
1 |
... |
1 |
...; |
||
ln2 |
ln2 |
ln4 |
|
|||||||||
|
|
|
|
|
lnn |
|||||||
2) |
lim an |
lim |
1 |
|
0. |
|
|
|||||
|
|
|
|
|||||||||
|
n |
|
|
n lnn |
|
|
||||||
Следовательно, по признаку Лейбница ряд сходится.
Так как ряд из абсолютных величин расходится, то исследуемый
ряд ( 1)n сходится условно;
n 2 lnn
14
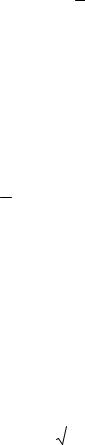
в) так как lim an |
lim |
2n 1 |
|
2 |
0, то не выполняется необходи- |
|
|
||||
n |
n 3n 2 |
3 |
|
||
мый признак сходимости ряда, следовательно, данный ряд расходится;
г) исследуем ряд из абсолютных величин
|
|
|
n 1 1 |
|
|
|
1 |
. |
|
|
|
( 1) |
|
|
|
|
|
|
|
|
|
|
|||||||
n 1 |
|
|
|
n 7n |
|
|
n 1n 7n |
|
|
|
|
|
|
||||||
Так как в общем члене данного ряда содержится показательная функция, то применим признак Даламбера.
Имеем a |
n |
|
1 |
|
, a |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
. |
|||||
|
|
n |
|
|
|
|
|
|
n 1 |
|
|
|
n |
|
|||||||||||
|
|
|
|
n 7 |
n 1 |
|
(n |
1) 7 |
|
|
(n 1) 7 |
7 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
l lim |
a |
n 1 |
|
lim |
|
|
n 7n |
|
|
|
1 |
lim |
|
n |
|
|
1 |
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n an |
|
|
n (n 1) 7n 7 |
|
7n n 1 7 |
|
|
|
|
||||||||||||||||
Так как l 1 1, то по признаку Даламбера данный ряд сходится.
7
Следовательно, исходный ряд сходится абсолютно;
|
|
n 2 ( 1)n |
|
n 1 |
|
n ( 1)n |
( 1)n |
1 |
|
||||||||
д) ( 1) |
|
|
|
2 |
( 1) |
|
|
( 1) |
|
|
2 |
|
|
|
|
. |
|
|
|
|
|
n |
|
n |
|
n |
n |
||||||||
n 1 |
|
|
|
n |
n 1 |
|
n 1 |
|
n 1 |
|
|
||||||
( 1)n |
|
|
|
|
|
n 1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ряд 2 |
|
|
|
является условно сходящимся (см. пункт (а)), а ряд |
|||||||||||||
|
|
|
|||||||||||||||
n 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 является гармоническим рядом, и он расходится.
n 1 n
Сумма сходящегося и расходящегося рядов представляет собой расходящийся ряд. Значит, исследуемый ряд расходится.
Пример 2. Исследовать на сходимость данные знакопеременные ряды и установить характер сходимости (абсолютная, условная):
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||
а) |
cosn |
; |
|
|
|
|
б) ( 1)n 1 |
|
; |
|
||||||||
3 |
|
|
|
|
|
n |
||||||||||||
n 1 n |
|
|
|
|
n 1 |
|
|
5 |
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
2n 1 |
|
||||||||||
в) ( 1)n |
|
|
; |
г) ( 1)n 1 |
. |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
||||||||||||||||
n 1 |
|
n |
n 1 |
|
|
|
n |
|||||||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
а) данный ряд является знакопеременным. Составим ряд из абсо- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
cosn |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
лютных величин членов данного ряда: |
|
|
|
|
. Сравним этот ряд |
|||||||||||||
|
|
|||||||||||||||||
|
|
3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
n |
||||||||
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
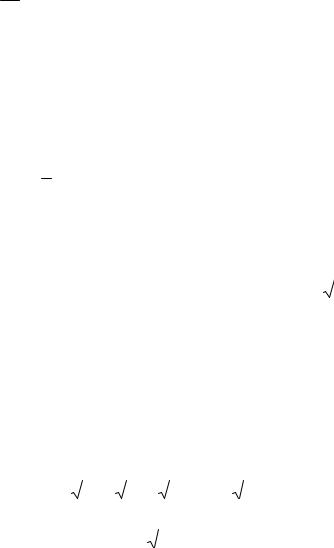
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с рядом |
, который сходится, так как является обобщенным гар- |
|||||||||||||||
3 |
||||||||||||||||
n 1 n |
|
|
|
|
|
cosn |
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|||||||||
моническим рядом |
|
|
при p 3 1. Учитываем, что |
|
|
|
|
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
||||||||||
|
p |
|
|
n |
3 |
|
|
n |
3 |
|||||||
|
|
n 1 n |
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, ряд, составленный из абсолютных величин членов данного ряда, сходится по первому признаку сравнения. Отсюда
следует, что данный ряд |
cosn |
абсолютно сходится; |
||
|
|
|||
n 1 n3 |
||||
|
|
|||
б) данный ряд является знакочередующимся.
Составим ряд из абсолютных величин членов данного ряда:
n . Так как в общем члене данного ряда содержится показательная
n 1 5n
функция, то применим признак Даламбера.
an |
|
n |
|
; |
|
an 1 |
n 1 |
. |
||
5n |
|
|
|
|||||||
|
|
|
|
|
|
|
5n 1 |
|||
l lim |
a |
n 1 |
lim |
(n 1)5n |
||||||
|
|
|
5n 1n |
|||||||
|
n an |
|
n |
|||||||
lim |
(n 1) 5n |
|
1 |
. |
5 5n n |
|
|||
n |
5 |
|
||
l 1 1, следовательно, ряд, составленный из абсолютных вели-
5
чин членов данного ряда, сходится. Значит, ряд абсолютно сходится; в) ряд является знакочередующимся. Составим ряд из абсолют-
|
|
|
|
|
1 |
|
|
|
ных величин членов данного ряда: |
|
. |
||||||
|
|
|
||||||
|
|
|
||||||
|
|
|
|
n 1 |
|
n |
||
Этот ряд расходится, так как является обобщенным гармониче- |
||||||||
|
|
1 |
|
|
|
|
|
|
ским рядом |
1 |
при p |
1. Следовательно, ряд не сходится абсо- |
|||||
p |
|
|||||||
n 1 n |
2 |
|
|
|
|
|
||
лютно.
Данный ряд удовлетворяет условиям признака Лейбница для знакочередующихся рядов:
1) 1 |
1 |
|
|
|
1 |
|
|
|
1 |
|
... |
1 |
|
...; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
3 |
|
|
4 |
|
|
|
|
|
n |
||||||||||||
2) lim an |
lim |
|
1 |
|
0. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
n |
|
n |
|
|
n |
|
|
|
|
|
||||||||||||||
Следовательно, ряд условно сходящийся; |
||||||||||||||||||||||||
г) данный ряд является знакочередующимся. |
||||||||||||||||||||||||
Так как |
lim an lim |
2n 1 |
2 0, то не выполняется необходимый |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
n n |
|
|
|
|
|
|||||||||||
признак сходимости ряда, следовательно, данный ряд расходится.
16

Задания для самостоятельной работы
1.Написать формулу общего члена для каждого из данных рядов:
1) 1 8 27 |
64 125 ...; |
2) |
2 |
|
|
4 |
|
|
8 |
19 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
...; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
7 |
|
9 |
|||||||||||||
3) |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||
0,1 0,02 |
0,003 0,0004 ...; |
4) |
1 |
|
|
4 |
|
9 |
|
|
|
16 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
...; |
||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
7 |
|
13 |
|||||||||||||||
|
|
1 |
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
10 |
|
|
|
|
|
|||||||||
5) |
|
|
|
|
|
.... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
9 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
4 5 |
|
14 11 |
19 19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. Найти частичную сумму Sn рядов, доказать их сходимость (по определению), найти сумму S ряда:
1)
n 1
3)
n 1
5)
n 1
7)
n 1
1 ; n(n 1)
1
;
(3n 2)(3n 1)
2
4n2 8n 3
;
2 n ; n(n 1)(n 2)
|
|
1 |
|
|
|
|
|
|
|
|
2) |
|
|
|
; |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
n 1 |
n(n 3) |
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|||
4) |
|
|
|
; |
|
|
||||
|
|
|
|
|
|
|
||||
|
n 1 |
(2n 1)(2n 5) |
|
|
||||||
|
|
3n 5 |
|
|
|
|
|
|
||
6) |
|
|
|
|
; |
|
|
|
||
|
2 |
|
|
|
|
|
||||
|
n 1 |
n(n |
1) |
|
|
|||||
|
|
|
|
|
n |
|
|
|||
8) |
|
|
|
|
|
|
. |
|||
|
(2n 1) |
2 |
(2n 1) |
2 |
||||||
|
n 1 |
|
|
|
|
|||||
3. Исследовать ряды на сходимость с помощью достаточного признака расходимости:
|
|
3n 1 |
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
1) |
|
; |
2) |
|
|
|
|
; |
3) cos |
; |
|
|
|
||||||
|
|
|
n 1 2n2 |
|
|
|
|
|
|
||||||||||
n 1 |
|
4n 2 |
|
1 |
n 1 |
|
|
n |
|
|
|
||||||||
|
|
n3 |
|
|
n 1 n |
|
n |
2 |
2 ln |
n2 |
3 |
||||||||
4) |
|
; |
|
5) |
|
|
|
|
|
; |
6) |
|
|
|
. |
||||
|
|
|
|
|
|
n2 |
|||||||||||||
|
|
|
|
|
|
||||||||||||||
|
2n 1 |
|
n 1 |
|
|
|
|
|
|
|
|||||||||
n 1 |
|
|
|
|
|
n 1 |
|
n 1 |
|
|
|
|
|
|
|
||||
4. Исследовать ряды на сходимость с помощью признаков сравнения:
|
|
1 |
|
|
|
|
|
|
|
|
4 2sinn |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||
1) |
|
|
|
; |
|
|
2) |
|
; |
3) |
|
|
|
|
|
|
|
; |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
n 1 |
3n 2 |
|
n 1 |
|
n lnn |
n 1 |
|
2 |
4n 5 |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
5 |
2cosn |
|
|
|
n |
|
3 |
|
|
|
|
|
|
|
||||||||||||
4) |
|
|
|
|
|
|
|
|
; |
5) |
|
; |
6) |
|
; |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
n 1 |
|
|
n |
2n |
|
|
|
|
5 3 |
|
|
|
|
|
4n |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
n |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7) sin |
; |
8) tg |
; |
9) |
|
|
|
|
|
|
; |
|
|
|||||||||||||||||||||||||||
n |
|
|
|
(2n 1)2 |
2n 1 |
|
|
|||||||||||||||||||||||||||||||||
n 1 |
|
|
|
2 |
|
|
|
|
|
|
|
n 1 |
|
|
4n |
n 1 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
3 |
n |
|
|
|
|
|
|
|
|
|
lnn |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
; |
|||||||
10) |
|
|
|
|
|
; |
|
|
11) |
|
; |
12) |
|
n 1 |
|
n 1 |
||||||||||||||||||||||||
22 n |
|
|
|
|
|
n |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n 2 3 |
|
n |
2 |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
|
|
arctgn3 |
|
n3 |
6 |
|
|
|
|
|
|
n |
2 1 |
|
||||||
|
|
|
3 narcsin |
|
|||||||||||||||||
13) |
|
|
|
|
; |
14) ln |
|
|
|
|
; |
15) |
|
|
|
|
; |
||||
|
|
|
|
3 |
|
|
4 |
|
|||||||||||||
|
n 1 n(n 2)(n 3) |
n 1 |
|
5 |
|
|
n 1 |
|
|
|
n |
2 |
|
||||||||
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16) |
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n 1 7n |
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Исследовать ряды на сходимость с помощью признака Даламбера:
|
|
|
1 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
2 |
|
|
|
|||
1) |
|
|
|
|
|
; |
2) |
; |
|
|
|
3) |
n |
; |
|
|
|||||||
|
|
|
|
|
|
n |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
n |
|
||||||||||||||
n 1 |
(2n 1)! |
n 1 |
2 |
|
|
|
|
|
n 1 |
3 |
|
|
|
||||||||||
|
|
|
3n |
|
|
|
|
|
|
2 5 ... (3n 1) |
|
|
(3n 1)! |
|
|||||||||
4) |
|
|
|
|
|
|
; |
5) |
|
|
; |
6) |
|
|
|
; |
|||||||
2 |
n |
(n |
|
1) |
1 5 ... (4n 3) |
|
8n n2 |
|
|||||||||||||||
n 1 |
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|||||
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
7) |
|
|
|
; |
|
|
|
8) |
|
|
|
. |
|
|
|
|
|
|
|
||||
3 |
n |
|
|
|
|
|
|
n |
(n 3)! |
|
|
|
|
|
|
|
|||||||
n 1 |
|
n! |
|
|
|
n 1 |
5 |
|
|
|
|
|
|
|
|
|
|||||||
6. Исследовать ряды на сходимость с помощью радикального признака Коши:
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
n n |
|
|
|
1 n2 |
|
||||||||||
1) |
|
|
|
|
|
|
|
|
|
; |
2) |
|
|
|
|
|
|
; |
3) 1 |
|
|
; |
||||||||||
ln |
n |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
n 1 |
|
|
|
(n 1) |
|
n 1 |
|
2n 1 |
|
n 1 |
|
n |
|
|
|||||||||||||||||
|
|
1 n 1 |
n2 |
|
|
|
|
|
|
n 1 |
|
|
3n 1 n |
|||||||||||||||||||
4) |
|
|
|
|
|
|
|
|
|
|
; |
5) arcsin |
|
|
|
|
; |
6) |
|
|
|
|
|
; |
||||||||
|
2 |
n |
|
|
|
|
|
|
n |
|
|
|
||||||||||||||||||||
|
n 1 |
|
|
|
n |
|
|
n 1 |
|
|
|
|
|
|
|
|
n 1 2n 1 |
|
||||||||||||||
|
|
n2 32 |
|
|
|
|
|
3n2 2 2n2 |
|
|
|
|
|
|
|
|||||||||||||||||
7) |
|
|
|
|
|
; |
|
|
|
8) |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
n 1 |
|
|
|
|
|
2 |
5 |
|
|
|
|
|
|
|
|||||||||||||||
|
n 1 5 |
|
|
|
|
|
|
|
|
|
n 1 |
n |
|
|
|
|
|
|
|
|
|
|||||||||||
7. Исследовать ряды на сходимость с помощью интегрального признака Коши:
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|||
1) |
|
|
|
|
|
; |
|
2) |
|
|
; |
|
|
3) |
|
|
|
; |
|
|
|||||||
|
(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
n 1 |
|
n 1 |
|
n 2 |
|
nlnn |
|
|
n 2 |
n lnn |
|
|
||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||||
4) |
|
|
; |
|
|
|
|
5) |
|
|
|
; |
|
6) |
|
|
|
|
; |
||||||||
n |
2 |
|
|
|
|
n |
2 |
2n 5 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
n 1 |
|
1 |
|
|
|
|
n 1 |
|
|
|
n 1 4 (4n 5)3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
7) |
n 3 |
|
|
|
; |
8) n 3 |
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
(n 1)ln(2n 1) |
|
nlnn(lnlnn)2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
18

8. Исследовать ряды на абсолютную и условную сходимость:
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|||||||||
1) ( 1)n 1 |
|
|
|
|
; |
|
|
2) ( 1)n 1 |
|
|
|
|
|
|
; |
3) ( 1)n 1 |
|
; |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(2n 1) |
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
3n 1 |
n 1 |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
5n 2 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
sinn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4) ( 1)n 1 |
|
|
|
|
; |
|
|
|
|
5) |
; |
|
|
|
|
|
|
|
|
|
|
6) |
sinn |
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n 1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 (ln3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lnn |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
7) |
cosn |
; |
|
|
|
|
|
|
|
|
|
|
|
8) ( 1)n 1 |
; |
|
|
|
|
9) ( 1)n 1 |
|
; |
|
|
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln(n 1) |
|
|
||||||||||||||||||||||||||||||||
n 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
n 1 |
n |
3 |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
2 |
n |
|
|
|
|
|
|
|
|
n 1 n |
|
n |
|
|||||||||||||||||||||||
10) ( 1) |
|
|
; |
|
|
|
|
|
11) ( 1) |
|
|
|
; |
|
|
|
|
12) |
|
( 1) |
|
|
; |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
|
|
|||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
||||||||||
13) |
( 1)n |
sinn2 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|||||||||||||||||||||
n |
|
|
|
|
n |
|
|
|
|
|
2 |
|
|
|
|
|
|
n 1 |
3n |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
14) |
( |
|
|
sin |
|
|
; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
2 |
|
|
|
n |
|
1) |
|
|
|
|
3 |
n |
15) ( 1) |
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
19
