Burlakova_Matematika_ryadi

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Государственный университет — учебно-научно-производственный комплекс (бывш. ОрелГТУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Так как lim

1 0, то исследуемый ряд расходится;

.pdf

Скачиваний:

Добавлен:

28.03.2015

Размер:

523.82 Кб

Скачать

☆

1 / 61 2 3 4 5 6 > Следующая >>>

Е.А. Бурлакова Л.В. Кузьмина

МАТЕМАТИКА.

РЯДЫ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ - УЧЕБНО-НАУЧНО- ПРОИЗВОДСТВЕННЫЙ КОМПЛЕКС»

Е.А. Бурлакова, Л.В. Кузьмина

МАТЕМАТИКА.

РЯДЫ

Рекомендовано ФГБОУ ВПО «Госуниверситет - УНПК» для использования в учебном процессе в качестве учебно-методического пособия

для высшего профессионального образования

Орел 2013

УДК 517.5(075) ББК 22.16я7 Б91

Рецензенты:

кандидат физико-математических наук, доцент кафедры «Высшая математика»

Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Государственный университет - учебно-научно- производственный комплекс»

Е.Ю. Тюлькина,

кандидат педагогических наук, доцент кафедры «Математика и математические методы в управлении» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации» (Орловский филиал)

И.В. Гайдамакина

Бурлакова, Е.А.

Б91 Математика. Ряды: учебно-методическое пособие для высшего профессионального образования / Е.А. Бурлакова, Л.В. Кузьмина. – Орел: ФГБОУ ВПО «Госуниверситет - УНПК», 2013. –

50с.

ISBN 978-5-93932-605-6

Содержание учебно-методического пособия охватывает следующие разделы программы дисциплины «Высшая математика»: числовые, функциональные, степенные ряды, ряды Фурье. Большое число решенных типовых задач облегчает подготовку к практическим занятиям и контрольным работам, а также выполнение контрольных работ студентамизаочниками. Задачи для самостоятельной работы позволяют закреплять навыки решения, компоновать задания для контрольных и самостоятельных работ.

Предназначено для студентов экономических и технических направлений подготовки очной и заочной форм обучения, а также для лиц, самостоятельно изучающих тему «Ряды» в курсе дисциплин «Математика», «Высшая математика», «Математический анализ» и др.

УДК 517.5(075) ББК 22.16я7

ISBN 978-5-93932-605-6 © ФГБОУ ВПО «Госуниверситет - УНПК», 2013

СОДЕРЖАНИЕ
Введение...................................................................................................	4
1.Числовые ряды......................................................................................	5
1.1. Сходимость и сумма ряда. Необходимый признак
сходимости ряда. Достаточный признак расходимости ряда.........	5
1.2. Достаточные признаки сходимости.............................................	8
1.3. Знакопеременные и знакочередующиеся ряды.........................	13
Признак Лейбница. Абсолютная и условная сходимость...............	13
Задания для самостоятельной работы...............................................	17
2.Функциональные ряды. Степенные ряды.........................................	20
2.1. Область сходимости функционального ряда............................	20
2.2. Интервал и радиус сходимости степенного ряда .....................	24
2.3. Вычисление суммы функциональных рядов ............................	26

2.4.Ряды Тейлора и Маклорена. Разложение функций

встепенной ряд. Приложения степенных рядов

для приближенных вычислений........................................................	28
Задания для самостоятельной работы...............................................	34
3. Ряды Фурье.........................................................................................	37
Задания для самостоятельной работы...............................................	41
Литература .............................................................................................	43
Приложение 1. Числовые ряды.............................................................	44
Приложение 2. Функциональные ряды. Степенные ряды..................	46
Приложение 3. Ряды Фурье ..................................................................	48

ВВЕДЕНИЕ

Последние несколько лет работа высшей школы в нашей стране отмечена значительным уменьшением объёма часов, отводимых действующими учебными планами на чтение лекций и проведение семинарских и практических занятий. В этих условиях возникает вопрос: как организовать изучение вузовских дисциплин, в частности, математики студентами. Одним из путей решения этой проблемы, безусловно, является совершенствование форм самостоятельной работы студентов.

Вданном учебно-методическом пособие разобраны основные типы заданий по теме «Ряды», которые позволят самостоятельно изучить данную тему, а потом закрепить ее с помощью задач для самостоятельного изучения. Но прежде чем решать задачи, студенту необходимо изучить соответствующий раздел теории и ответить на вопросы к каждой теме, а затем внимательно, с выполнением всех действий на бумаге, разобрать решенные задачи.

Внастоящем пособии приведены также приложения, содержащие краткий теоретический материал по каждой теме. Пособие может быть полезно и для преподавателей, ведущих практические занятия.

1. ЧИСЛОВЫЕ РЯДЫ

Контрольные вопросы для самопроверки

1.Что называется числовым рядом, общим членом ряда?

2.Что называется n-й частичной суммой ряда и суммой ряда?

3.Что называется n-м остатком ряда?

4.Какой ряд называется сходящимся; расходящимся?

5.Сформулируйте необходимый признак сходимости ряда.

6.Сформулируйте достаточное условие расходимости ряда.

7.Какой ряд называется гармоническим; обобщенным гармоническим?

8.Какой ряд называется геометрическим?

9.Сформулируйте достаточные признаки сходимости, основанные на сравнении рядов с положительными членами.

10.Сформулируйте признак Даламбера о сходимости ряда с положительными членами.

11.Сформулируйте радикальный признак Коши о сходимости ряда с положительными членами.

12.Сформулируйте интегральный признак Коши о сходимости ряда с положительными членами.

13.Какой ряд называется знакопеременным; знакочередующим-

ся?

14.Сформулируйте признак Лейбница: достаточное условие сходимости знакочередующегося ряда.

15.Какой ряд называется абсолютно сходящимся; условно сходящимся?

1.1.Сходимость и сумма ряда. Необходимый признак сходимости ряда. Достаточный признак расходимости ряда

Примеры решения задач

Пример 1. Написать четыре первых члена ряда по заданному об-

щему члену аn					1			.
щему члену аn								.
					n(n 1)
Решение: последовательно подставляя в формулу общего члена
значения n = 1, 2, 3, 4,								получим:
а		1	; а			1	; а		1	; а			1	.
а			; а				; а			; а			1	.
1	1 2			2		2 3		3	3 4		4		4 5
												5

Пример 2. Написать формулу общего члена для каждого ряда:


а) 1			1		1		1			1	...;
					2	2	23			24
		2
б)	2			4		6		8	... .
							14
5		8			11

Решение:

а) знаменатели членов данного ряда могут быть получены из формулы 2n 1, где n = 1, 2, 3, … . Следовательно, общий член an 21n 1 ;

б) числители членов данного ряда – чётные числа вида 2n, а знаменатели – числа, которые могут быть получены по формуле 3n 2.

Следовательно, общий член an	2n	.

	3n 2

Пример 3. Найти частичную сумму Sn ряда, доказать его сходимость (по определению), найти сумму S ряда:

	1				2n 1
а)		;	б)				.
	(2n 1)(2n 1)			n	2	2
n 1			n 1		(n 1)

Решение:

а) n-й член ряда an (2n 1)(2n 1) является правильной рацио- нальной дробью относительно n. Разложим аn на сумму простейших дробей:

1	A	B	.
(2n 1)(2n 1)
	2n 1	2n 1

Найдём коэффициенты А и В. Применим метод задания частных значений, полагая последовательно в полученном тождестве n 1

		1					1										1			1		2
и n		1	: при n				1		имеем				1 2A;			A	1	; при n			имеем	1 2B;
и n			: при n						имеем				1 2A;			A		; при n			имеем	1 2B;
1	2					2										2			2
1						1			1				1
B	. Итак, an													.
B	. Итак, an								2n 1			2n 1		.
2						2			2n 1			2n 1
Тогда Sn					1				1		1		...			1			=
Тогда Sn								3 5		5 7			...		(2n 1)(2n 1)				=
				1 3				3 5		5 7					(2n 1)(2n 1)
														6

	1				1			1		1			1		1			1		1			1			1
			1														...							1			.
			1		3			3		5							...		2n 1	2n 1			2	1			.
	2				3			3		5			5 7						2n 1	2n 1			2			2n 1
S lim Sn									1				1				1	.
						lim				1
						lim				1		2n 1					2
			n				n 2					2n 1					2
																		1
Следовательно,											ряд			n 1				1		сходится				и		сумма его
Следовательно,											ряд					(2n 1)(2n 1)				сходится				и		сумма его
		1														(2n 1)(2n 1)
равна		1		;
равна				;
	2																				1		1
б) член ряда an										можно представить в виде											1		1		.
б) член ряда an										можно представить в виде											n2	(n 1)2			.
																					n2	(n 1)2

Тогда

Sn		3			5									7		...					2n 1

	1 22					22	32						32	42						n2(n 1)2
		1				1				1				1				1						1			1
		1				1				1				1				1				1		1			1

1			2				2				2					2			2						2	1		2 .
1		2	2				2		3		2					2		4	2		...		2	(n 1)	2	1	(n 1)	2 .
		2				2			3					3				4			n			(n 1)			(n 1)
														1			1.
S lim Sn					lim									1
															2
								1				(n		1)	2
n						n						(n		1)
Ряд				2n 1						сходится и сумма его равна 1.
Ряд	n 1 n2(n 1)2									сходится и сумма его равна 1.
	n 1 n2(n 1)2

Пример 4. Исследовать на сходимость ряды с помощью достаточного признака расходимости ряда:

2n 1

2 n

а)

;

б) 1

n 1

Решение:

2n 1

а) так как lim an

lim

то выполняется достаточный

признак расходимости ряда, следовательно, ряд

2n 1

расходится;

n 1

2 2

б) так как lim an lim 1

lim

0, то выполняет-

ся признак расходимости, следовательно, данный ряд расходится.

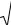
1.2. Достаточные признаки сходимости

Примеры решения задач

Пример 1. Исследовать на сходимость следующие ряды с помощью признаков сравнения:

а)

;

б)

;

n 1

8n 10

n 1

n 3

в)

;

г)

;

6(n

n 2

ln n

n 1

д)

;

е) sin

;

n 1

3n 1

n 1

ж) ln 1

;

и)

n 1

n 1n2sin2 n

Решение:

а) сравним данный ряд со сходящимся рядом

, который яв-

ляется обобщенным гармоническим рядом

n 1

при p 2 1.

n 1

Общий член данного ряда an

меньше общего члена

n2 8n 10

обобщенного гармонического b

, то есть a

b ,

n2 8n 10 n2

который сходится. Следовательно, по первому признаку сравнения данный ряд также сходится;

								1
б) сравним данный ряд с геометрическим рядом								1	, который
б) сравним данный ряд с геометрическим рядом								n	, который
	1		1	1		n 1		3
сходится, так как q	1	1, и учитываем, что	1	1	.
3			n 3n	3n
Следовательно, по первому признаку сравнения данный ряд так-
же сходится;						1

в) сравним данный ряд с гармоническим рядом							.
в) сравним данный ряд с гармоническим рядом							.
				n 1		n
8

Так как гармонический ряд расходится и		1	1	, то по первому
Так как гармонический ряд расходится и		ln n	n	, то по первому
		ln n	n
признаку сравнения исходный ряд также расходится;
г) числитель и знаменатель дроби	n 5	неограниченно растут
г) числитель и знаменатель дроби	6(n4 1)	неограниченно растут
	6(n4 1)

при n . Скорость роста числителя определяется слагаемым n, так что можно записать n 5~ n, при n . Аналогично для знаменателя

n4 1~ n4, при n . Таким образом,	(n 5) ~ n	~	n	1	.
n4 1~ n4, при n . Таким образом,	6(n4 1) ~ n4	~	n4		.
	6(n4 1) ~ n4		n4	n3
						1
Сравним данный ряд с обобщенным гармоническим рядом						1	.
Сравним данный ряд с обобщенным гармоническим рядом						3	.
					n 1	n

Этот ряд сходится, так как p 3 1. Применим второй признак сравнения, полагая

Тогда lim an lim

n b	n
n

(n 5) n3

6(n4 1) 1


n 5		,	b		1		.
6(n4 1)
			n		n3
lim	n4	5n3				1		0.
			6
n 6n4				6

Следовательно, данный ряд сходится;

д)

аналогично

пункту г) находим ряд для сравнения,

то есть

. Тогда сравним данный ряд с расходящимся гармониче-

(3n 1) ~ n

ским рядом

n 1

Применим второй признак сравнения, полагая a

;

3n 1

Тогда

lim

Следовательно,

исследуемый ряд

n b

n 3n 1

также расходится;

е)

общий член данного ряда

an sin

эквивалентен при

дроби 1 . Сравним данный ряд с расходящимся гармоническим рядом

1. Применим второй признак сравнения.

n 1n

1 / 61 2 3 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.03.20151.89 Mб26Bobylev_kulturarechi_2001.pdf
#
28.03.20151.13 Mб153bobylev_kyltura_rechi_1.pdf
#
28.03.20151.41 Mб19Bobylev_prakt_po_ritor.pdf
#
12.03.20162.41 Mб45Bodrov.rtf
#
15.12.2018195.5 Кб6BO_vse_temy.docx
#
28.03.2015523.82 Кб9Burlakova_Matematika_ryadi.pdf
#
24.09.2019158.72 Кб3BZhD_1.doc
#
28.03.2015506.88 Кб60Chernova_statistika_1.doc
#
11.11.2019639.49 Кб8Chernova_statistika_2.doc
#
09.11.201965.39 Кб4Chistovik.docx
#
28.03.20151.83 Mб12chistyakov.doc