Ответ: экстремум не существует.

Пример 20. Исследовать на экстремум функции

.

Решение. 1). О.О.Ф.: х  1.

2).

3). а) прих = 3 или при х = -1.

б) не существует прих = 1, но эта точка не принадлежит О.О.Ф.

4). Отметим на координатной прямой критические точки х = -1, х = 3, х = 1.

5). Знаки производной отметим на полученных промежутках.

6). х = -1 – точка максимума, у_тах = -8

х = 3 – точка минимума, у_min = 0.

Ответ: x_max = -1, y_max =-8;

x_min = 3, y_min = 0.

§ 4. Наибольшее и наименьшее значения непрерывной функции на отрезке.

4.1. Справочный материал.

1. Наибольшим (наименьшим) значением функции y=f(x) на промежутке X называется такое число M(m), что существует такая точка x₀, принадлежащая этому промежутку, что для всехx из этого промежутка.

2. Наибольшее и наименьшее значения функции на промежутке X дифференцируемая функция f(x) может принимать либо на концах промежутка (если это числа), либо в критических точках, лежащих внутри промежутка.

3. На рис.1 функция y=f(x) достигает наибольшее значение на отрезке [a;b] в точке x=a и наименьшее значение в точке x=b:

На интервале (a;b) в этом случае функция не достигает ни наименьшего ни наибольшего значений.

4. Если дифференцируемая функция f(x) на промежутке X имеет единственную точку экстремума и в этот экстремум – максимум (минимум), то в этой точке достигается наибольшее (наименьшее) значение функции.

5. На рис.1 функция y=f(x) на отрезке [x₁;x₃] в точке x=x₂ имеет единственный максимум:

Функция y=f(x) на отрезке [x₂;x₄] в точке x=x₃ имеет единственный минимум:

4.2 Схема нахождения наибольшего и наименьшего значений функции .

1. Найти О.О.Ф.

2. Найти в О.О.Ф.

3. Найти критические точки в О.О.Ф.:

4. а).в которых выполняется равенство ;

5. б) в которых 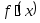не существует.

6. Изобразить на числовой оси О.О.Ф. и все ее критические точки.

7. Определить интервалы знакопостоянства производной в каждом из промежутков на которые критические точки разбивают О.О.Ф.

8. На основании достаточных условий экстремума сделать заключение о экстремуме функции в каждой из указанных в п.3 критических точках.

9. Найти значения функции в критических точках внутри промежутка и на концах промежутка (если это числа).

10. Из всех найденных значений в п.7 выбрать наибольшее и наименьшее значения.

Пример 21. Найти наибольшее и наименьшее значения функции на отрезке [-2; 2].

Решение. О.О.Ф.: х  R;

х₁ = -1, х₂ = 3 – критические точки; x₁ = -1  [-2; 2], x₂ = 3  [-2; 2].

х₁ = -1 – единственная критическая точка на [-2; 2].

у(-1)=(-1)³-3(-1)²-9(-1)+2=-1-3+9+2=7 (наибольшее);

у(2)= (2)³-3(2)²-9(2)+2=8-12-18+2=-20 (наименьшее);

у(-2)= (-2)³-3(-2)²-9(-2)+2=-8-12+18+2=0. Ответ:

Пример 22. Найти наибольшее и наименьшее значения функции на промежутке [1; 3).

Решение. О.О.Ф.: x  R;

х₁ = 0, х₂ =-1 – критические точки.

на [1; 3).

На промежутке [1; 3) данная функция убывает:

у(1) = -2(1)³ -3(1)² + 4 = -2-3+4 = -1.

Наибольшее значение функция достигает на левом конце промежутка:

.

Наименьшее значение в промежутке [1; 3) функция не достигает, так как точка х =3 не принадлежит этому промежутку.

Ответ:

Пример 23. Требуется огородить проволочной сеткой длины 32 м прямоугольный участок, прилегающий к стене. Найти размеры участка, при которых его площадь будет наибольшей.

Решение. Обозначим стороны прямоугольника через АВ = СD = x, BC = AD = y. Тогда его площадь S = xy.

Так как 2х + у = 32, получим Тогда. Найдем О.О.Ф. площади:

.

Найдем наибольшее значение функции S на интервале (0; 16).

х = 8 – единственная критическая точка.

х = 8 – единственная точка максимума, значит

.

Размеры участка: ширина – х = 8; длина – у = 32-16=16.