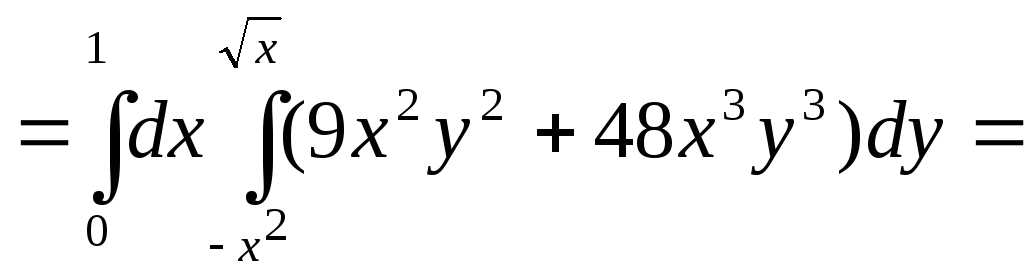- •Содержание
- •Пояснительная записка
- •1. Кратные интегралы
- •1.1. Двойные интегралы Основные свойства двойного интеграла
- •Вычисление двойного интеграла
- •Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах
- •1.2. Тройные интегралы
- •Вычисление тройного интеграла
- •Тройной интеграл в цилиндрических координатах
- •2. Элементы теории поля
- •3. Ряды
- •Ряды с положительными членами
- •Знакопеременные ряды
- •Степенные ряды
- •Ряды Фурье
- •Ряды Фурье с периодом
- •4. Теория функций комплексного переменного. Операционное исчисление
- •4.1. Комплексные числа
- •Множества на комплексной плоскости
- •4.2. Функции комплексного переменного
- •4.3. Операционное исчисление
- •Применение операционного исчисления к решению дифференциальных уравнений
- •Контрольная работа №7. «Кратные интегралы»
- •Контрольная работа №8. «Элементы теории поля»
- •Контрольная работа №9. «Ряды»
- •Контрольная работа №10. «Функции комплексного переменного. Операционное исчисление»
- •Список литературы
Содержание
|
Предисловие……………………………………………………………………………………….. 3 | ||
|
1. |
Кратные интегралы………………………………………….………..……………………... |
4 |
|
|
1.1. Двойные интегралы……...……………………………………………………………... |
4 |
|
|
1.2. Тройные интегралы…...………………………………………………………………... |
7 |
|
2. |
Элементы теории поля……………………………………………….……………………... |
9 |
|
3. |
Ряды……………………………………………………………..…...………………………. |
14 |
|
4. |
Теория функций комплексного переменного. Операционное исчисление……..……….. |
23 |
|
|
4.1. Комплексные числа……...……………………………………………………………... |
23 |
|
|
4.2. Функции комплексного переменного..………………………………………………... |
26 |
|
|
4.3. Операционное исчисление……………………………………………………………... |
30 |
|
Контрольная работа №7…………………………………………………………………………... |
35 | |
|
Контрольная работа №8…………………………………………………………………………... |
40 | |
|
Контрольная работа №9…………………………………………………………………………... |
44 | |
|
Контрольная работа №10………………………………………………………………………... |
48 | |
|
Список литературы…...…………………………………………………………………………… |
56 | |
Пояснительная записка
Цель преподавания математики в вузе – ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач; привить студентам умение самостоятельно изучать учебную литературу по математике и ее приложениям; развить логическое мышление и повысить общий уровень математической культуры; выработать навыки математического исследования прикладных вопросов и умение перевести задачу на математический язык.
Настоящее пособие для студентов очно-заочной и ускоренной формы обучения всех технических специальностей содержит методические указания и контрольные задания по курсам интегрального исчисления, теории поля, рядов, теории функций комплексного переменного, операционного исчисления.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса по учебной литературе, рекомендуемой в данном пособии.
Каждая задача контрольной работы содержит по 30 вариантов. Номер варианта расчетной работы определяется по последним двум цифрам номера зачетной книжки студента и соответствует этим цифрам, если они образуют число от 01 до 30. Если же число больше 30, то номер варианта равен остатку после деления этого числа на тридцать. Если же в остатке получен ноль, тогда ваш вариант 30.
1. Кратные интегралы
1.1. Двойные интегралы Основные свойства двойного интеграла
1.
![]() .
.
2.
![]() ,
где
,
где![]() - постоянная.
- постоянная.
3.
Если область
![]() разбита на две области
разбита на две области![]() и
и![]() ,
то
,
то
![]() .
.
4.
Если
![]() ,
то
,
то![]() - площадь области
- площадь области![]() .
.
Вычисление двойного интеграла
Различают два основных вида области интегрирования.
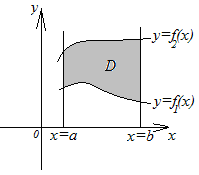
1.
Область интегрирования
![]() ограничена слева и справа прямыми
ограничена слева и справа прямыми![]() и
и![]() (
(![]() ),
а снизу и сверху непрерывными кривыми
),
а снизу и сверху непрерывными кривыми![]() и
и![]() (
(![]() ),
каждая из которых
),
каждая из которых
|
|
пересекается вертикальной прямой только в одной точке (рис. 1.1). Для такой области двойной интеграл вычисляется по формуле
причем
сначала вычисляется внутренний
интеграл
|
|
рис. 1.1 |
2.
Область интегрирования
![]() ограничена снизу и сверху прямыми
ограничена снизу и сверху прямыми![]() и
и![]() (
(![]() ),
а слева и справа непрерывными кривыми
),
а слева и справа непрерывными кривыми![]() и
и![]() (
(![]() ),
каждая из
),
каждая из
|
|
которых пересекается горизонтальной прямой только в одной точке (рис. 1.2). Для такой области двойной интеграл вычисляется по формуле
причем
сначала вычисляется внутренний
интеграл
|
|
рис. 1.2 |
Правые части указанных формул называются повторными (или двукратными) интегралами.
В более общем случае область интегрирования с помощью разбиения на части сводят к основным областям.
Пример 1.1. Построить область и изменить порядок интегрирования в интеграле
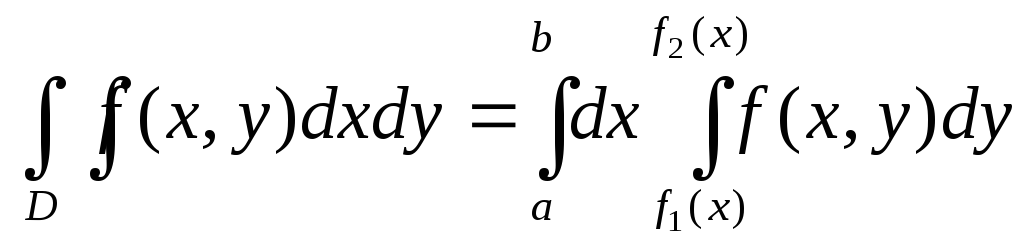 .
.
Решение.
Область
интегрирования ограничена линиями
![]() ,
,![]() ,
,![]() ,
,![]() .
.
|
рис. 1.3 |
Решая
совместно эти уравнения, находим
координаты
Изменим
порядок интегрирования. Внешнее
интегрирование теперь будет производиться
по переменной
В
области
В
области
В
области
|
(нижний
и верхний пределы внешнего интеграла),
а
![]() .
.
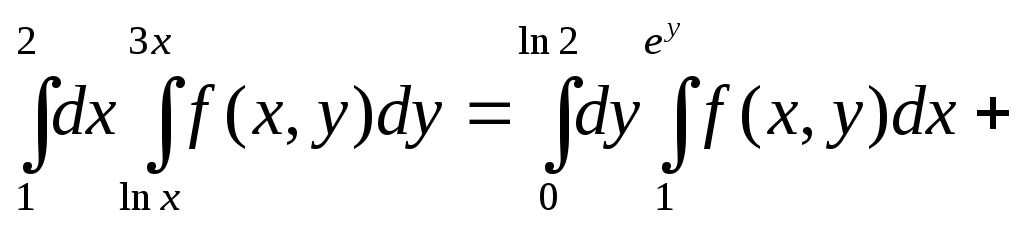
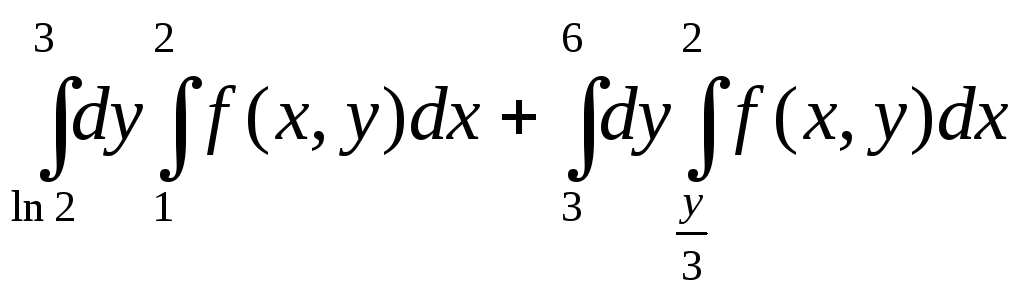 .
.
Пример 1.2. Вычислить интеграл
![]() ;
;
![]() .
.
Решение.
Область
интегрирования
![]() изображена на рис. 1.4). Расставим пределы
изображена на рис. 1.4). Расставим пределы
|
рис. 1.4 |
интегрирования и вычислим интеграл:
|

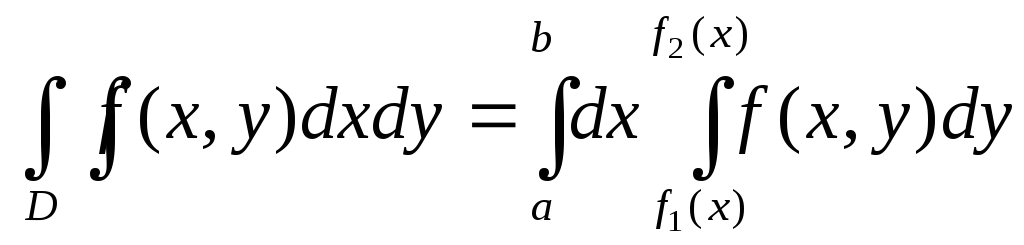 ,
,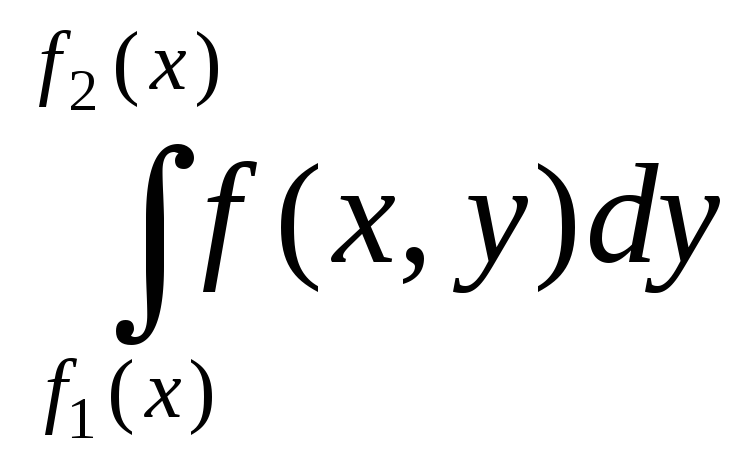 ,
в котором
,
в котором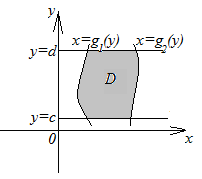
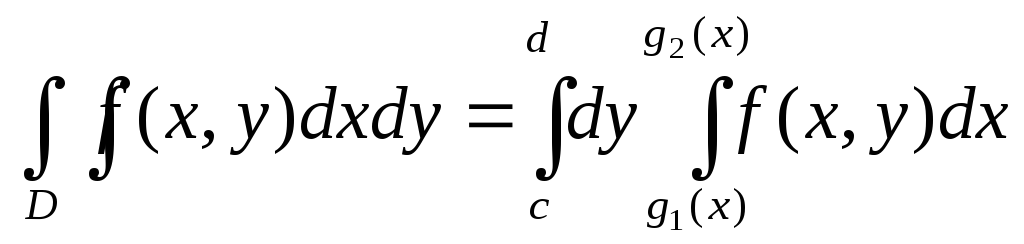 ,
,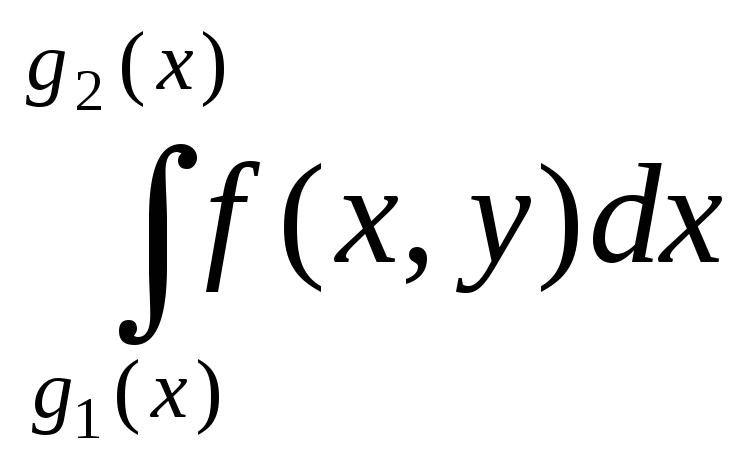 ,
в котором
,
в котором