2.12. Движение свободной частицы

Рассмотрим наиболее простую ситуацию: на движущуюся частицу не действуют никакие силы, т.е. она полностью свободна.

Потенциальная энергия частицы в этом случае равна 0.

Пусть частица с энергией Е движется в направлении х. Тогда уравнение Шредингера принимает очень простой вид

Частным решением этого уравнения является функция c собственным значением энергии(в этом можно убедиться подстановкой), где

Полная волновая функция свободной частицы имеет вид

т.е. свободная частица на языке квантовой механики отображается как плоская монохроматическая волна с циклической частотой  = Е/ħ и волновым числом k = р/ħ.

Вероятность обнаружения частицы в какой-либо области пространства определяется величиной ². В данном случае . Квадрат модуля функции равен:

Этот результат говорит, что вероятность обнаружения частицы в любой точке оси х одинакова. Следовательно, область движения частицы вдоль оси х ничем не ограничена.

Нет для свободной частицы и ограничений на величину энергии. Ее энергия может принимать любые значения.

2.13. Отражение частицы от потенциальной ступеньки

Перейдем к рассмотрению частиц, движущихся в потенциальном поле. Начнем с простейшей ситуации.

Пусть частица движется слева направо вдоль оси х. В области х < 0 ее потенциальная энергия U = 0, а в области х0 U = U₀.

В классическом случае частица с энергией E < U₀ в точке х = 0 должна отразиться. Если же E > U₀, то скорость частицы должна уменьшиться, а направление движения не должно измениться ().

Д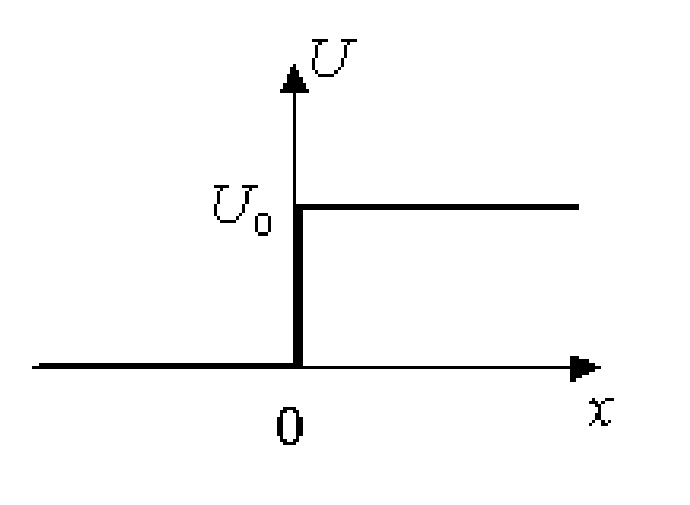ля того чтобы оценить поведение квантовой частицы с энергиейE<U_o, нам необходимо решить уравнение Шрёдингера и найти волновую функцию . В данном случае его удобно решать для x < 0 (область 1) и для х  0 (область 2).

Уравнения для этих областей будут иметь вид

,

Решения этих уравнений имеют следующий вид:

,

,

где ,.

Рассмотрим эти решения.

В выражении для расчета ₁ первое слагаемое описывает волну, идущую слева направо, а второе – волну, распространяющуюся справа налево. Это позволяет сделать вывод: квантовая частица должна отразиться от барьера (точно так же, как и классическая частица).

Теперь рассмотрим уравнение для ₂. В этом уравнении второй член () с увеличениемх неограниченно растет. Но это означает, что вероятность обнаружить частицу растет по мере углубления в область 2. Это физически недопустимо. Поэтому мы полагаем, что В₂ = 0.

Первое слагаемое в ₂ ведет себя нормально –- по мере роста х оно уменьшается.

Найдем А₁, В₁, А₂.

Очевидно, вероятность обнаружения частицы не должна меняться скачком. Следовательно, ₁(0)=₂(0) и .

Отсюда

А₁ + В₁ = A₂;

ik₁A₁ – ik₁B₁= –A₂ = –(A₁ + B₁);

ik₁A₁ – ik₁B₁ = –A₁ – B₁;

A₁(ik₁ + ) = B₁(ik₁ – );

;

Таким образом, волновые функции ₁ и ₂ имеют вид

,

Оценим вероятность нахождения частицы в первой и второй областях.

Функция ₁ содержит два слагаемых – с А₁ и с В₁, описывающих соответственно падающую и отраженную волны.

Квадрат модуля первого слагаемого равен А₁².

Квадрат модуля второго слагаемого .

Таким образом, амплитуды падающей и отраженной волн одинаковы. Это значит, что частица с энергией E < U_o обязательно отразится от потенциальной ступеньки.

Для ₂

,

Из выражения для расчета видно, что вероятность обнаружения частицы во второй области экспоненциально уменьшается с ростомх.

Но это означает, что частица может проникать на некоторую глубину за потенциальную ступеньку!

Классическая частица с энергией E<U_oни при каких условиях не может оказаться за потенциальным барьером.

Квантовая частица с такой же энергией вполне может оказаться за непреодолимым барьером. Исключено это лишь в том случае, когда потенциальный барьер бесконечно высок (с ростомU_oувеличивается, поэтому глубина проникновения за потенциальный барьер с ростомU_oуменьшается; приU_o =₂(x) = 0).

Таким образом, поведение квантовой частицы существенно отличается от поведения классической частицы.

Если энергия частицы больше высоты потенциальной ступеньки (т.е. E > U₀), то решение уравнения Шредингера имеет вид

,

где , и.

Смысл слагаемых в ₁ тот же, что и в предыдущем случае.

Во второй области отраженной волне взяться неоткуда. Поэтому полагаем В₂ = 0 и

Используя условия непрерывности, можем записать

A₁ + B₁ = A₂;

k₁(A₁ – B₁) = k₂A₂;

;

.

Поскольку B₁  0, и в этом случае в области 1 имеется отраженная волна (хотя ступенька низкая, т.е. E > U_о).

Это означает, что квантовая частица может отразиться от потенциальной ступеньки, хотя ее энергии вполне достаточно для его преодоления. Классическая частица в таких условиях не отразится никогда (представьте себе артиллерийский снаряд, попавший в оконную раму и отскочивший назад из-за удара о оконное стекло).

Для количественной характеристики барьеров удобно пользоваться так называемым коэффициентом отражения 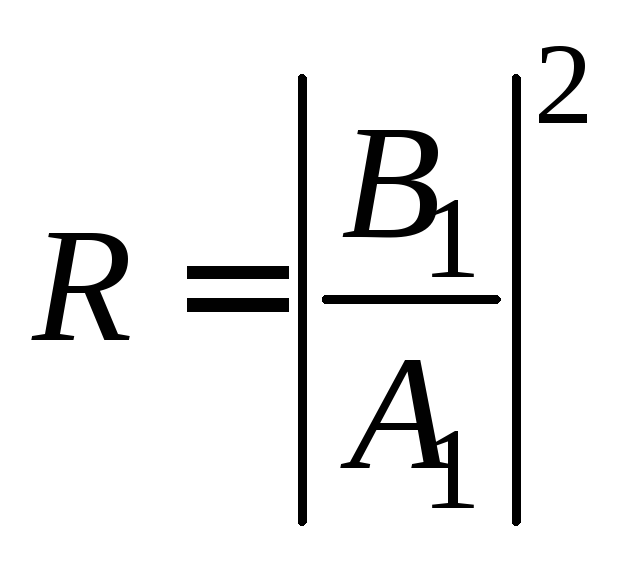. Этот коэффициент показывает, какова средняя вероятность отражения частицы от барьера.

В данном случае

Из полученного выражения следует, что вероятность отражения квантовой частицы от барьера зависит от соотношения энергии частицы и высоты потенциальной ступеньки.

При увеличении энергии частицы вероятность отражения от потенциальной ступеньки высотой U_о снижается.