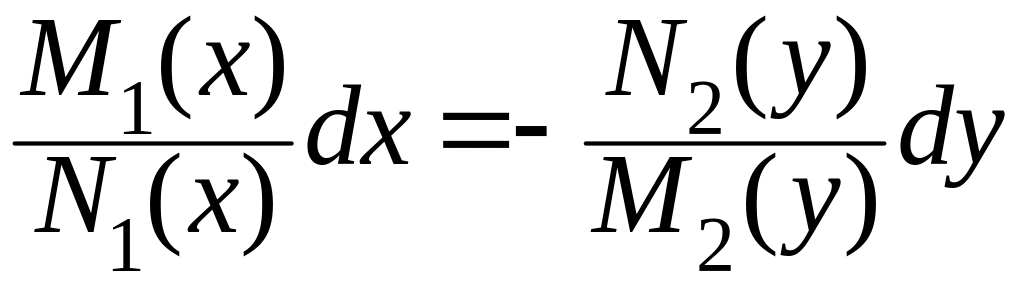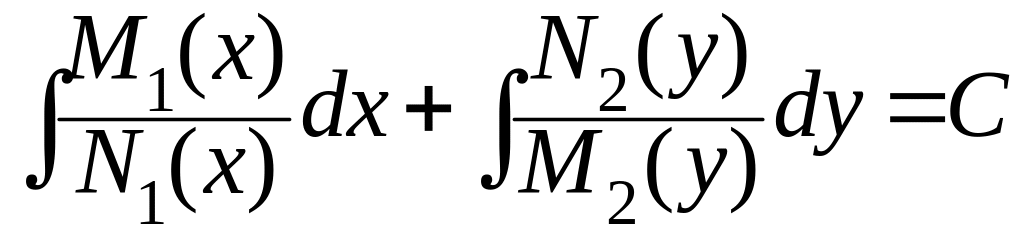§1. Основные понятия

Дифференциальным уравнением называется выражение вида:

(1) , связывающее независимую переменную , искомую функцию и ее производные

Порядком дифференциального уравнения называется порядок старшей производной

Пример 1: ДУ 4-го порядка

Функция называется решением (интегралом) дифференциального уравнения вида (1), если оно обращает его в верное тождество. (В некоторой области )

Определение. Общее решение уравнения n-го порядка , где - произвольные постоянные

Определение. Частное решение получается из общего, когда параметры принимают конкретные числовые значения

График решения дифференциального уравнения называется его интегральной кривой.

Процедура решения дифференциального уравнения называется его интегрированием.

Дифференциальным уравнением 1-го порядка называется выражение вида:

(2)

Определение. Нормальная форма: (2а) – разрешенная относительно

Определение. Условие вида называется начальным условием

Общее решение дифференциального уравнения 1-го порядка имеет вид:

Определение. Частное решение дифференциального уравнения 1-го порядка имеет вид: , где - конкретное числовое значение

Пример 2: Решение:

Определение. Пусть даны уравнения (2а) и начальные условия (3). Задача нахождения решения дифференциального уравнения (2а) удовлетворяющего начальным условиям (3), называется задачей Коши.

ТЕОРЕМА (о существовании и единственности решения дифференциального уравнения ) Пусть решение уравнения (2)/(2а) – функция и непрерывны в области . Тогда найдется такое значение , существующее и единственное решение дифференциального уравнения (2) удовлетворяющее начальному условию (3)

Геометрический смысл теоремы Коши: При выполнении условия теоремы всегда найдется, и притом единственная, интегральная кривая, проходящая через точку

Довольно часто дифференциальное уравнение не удается разрешить в элементарных функциях относительно произвольной постоянной. Тогда решение задается в виде

- общий интеграл этого уравнения.

Геометрический смысл дифференциального уравнения 1-го порядка:

В нормальной форме В фиксированной

Фактически задан угловой коэффициент касательной к интегральной прямой, говорят, что задано поле направлений. Таким образом с геометрической точки зрения решение дифференциального уравнения 1-го порядка представляет собой нахождение интегральных кривых, касательные к которым совпадают с направлением поля в данных точках.

Геометрическое место точек, в которых выполняется называется изоклиной данного дифференциального уравнения вида (2).

§2. Дифференциальные уравнения (ду) с разделяющимися переменными. Однородные уравнения.

Определение. Уравнения вида (1) называется ДУ первого порядка с разделяющимися переменными Схема решения:

;

где G(y) – первообразная от функции .

Общий интеграл имеет:

Определение. Дифференциальная форма ДУ первого порядка имеет вид:

ДУ первого порядка с разделяющимися переменными: