Уравнения, не содержащие функцию и её производные до k-1 порядка включительно. (*)
Обозначим
Решая последнее уравнение получим p, затем интегрируя k раз получим y.
Пример 1: Решить уравнение
Решение:
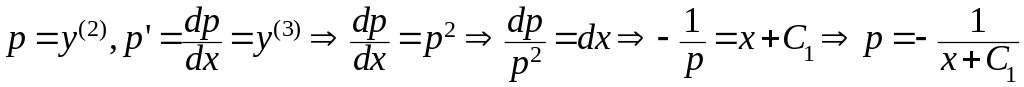
Уравнения, не содержащие независимую переменную:
Замена:
и т.д.
Пример 2: Решить уравнение:
.
Решение: Замена:
,
подставим:
,
частное решение
.
Получим общее решение:
Общее решение включает в себя также
частное решение
.
§5. Линейные однородные дифференциальные уравнения высших порядков (лоду).
Определение. Дифференциальное уравнение вида:
(5.1)
называется линейным дифференциальным уравнением n-ого порядка.
Если
линейное однородное дифференциальное
уравнение n-ого порядка.
Пусть
,
тогда на
ЛОДУ n-ого порядка
(5.2)
(5.2a)
(*)
Свойства лоду.
ТЕОРЕМА 5.1
Пусть
является решением ЛОДУ (5.2). Тогда
также является решением (5.2).
Доказательство: вытекает из первого свойства линейного дифференциального оператора.
ТЕОРЕМА 5.2 Пусть
и
являются решением ЛОДУ (5.2). Тогда
также является решением.
Доказательство: вытекает из второго свойства линейного дифференциального оператора.
Следствие: Пусть
решение ЛОДУ (5.2). Тогда их линейная
комбинация
также является решением ЛОДУ (5.2).
Определение. Любые
линейных независимых решений ЛОДУ
го
порядка называются его фундаментальной
системой решений (ФСР).
ТЕОРЕМА 6.3 Общее решение ЛОДУ (5.2)
го
порядка имеет вид
(6.3), где
- линейно независимые решения (5.2), а
-постоянный
коэффициент
Замечание. Таким образом общее
решение ЛОДУ является линейной комбинацией
его ФСР. Как вытекает из этих результатов,
множество всех решений ЛОДУ образует
мерное
линейное пространство для которого
любая ФСР является базисом.
Замечание. максимальное количество линейно независимых решений ЛОДУ го порядка равно
§7. Лоду с постоянными коэффициентами
Рассмотрим
(7.1)
Найдем вид общего решения в различных
случаях
-постоянных
-
является частным решением уравнения
(7.1)
-характеристическое
уравнение для (7.1)-(7.2)
Решения
характеристического уравнения при
подстановке в
дают частные решения уравнения (7.1),
причем все. Общее решение по теореме
6.3 является линейной комбинацией этих
частных решений. Таким образом, мы
свели задачу решения ЛОДУ с постоянными
коэффициентами к задаче нахождения
корней алгебраического уравнения
степени n.
Все корни различны и действительны
Имеем n различных корней
характеристического уравнения (7.2), им
соответствует n корней
.
Согласно примеру 6.2 эти функции линейно
независимы, следовательно образуют ФСР
ЛОДУ (7.1), следовательно по теореме 6.3
общее решение (7.1)
.
Пример 1
Решение. характеристическое уравнение
имеет вид:
- общее решение уравнения
Все корни различны, среди них есть комплексные
Комплексные корни уравнения (7.2) являются
сопряженными вида
им соответствуют корни (7.1) вида
тогда
подставляя решение этого вида в (7.1)
выделяя действительные и мнимые части
и приравнивая их к нулю, находим, что
указанной паре комплексных корней
соответствует решение (7.1) вида:
и
Пример 2
Решение. Характеристическое уравнение
имеет вид:
Тогда общее решение имеет вид:
