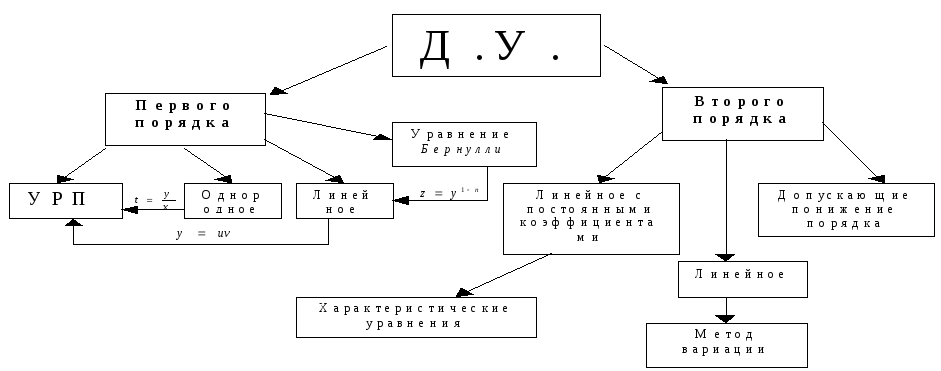
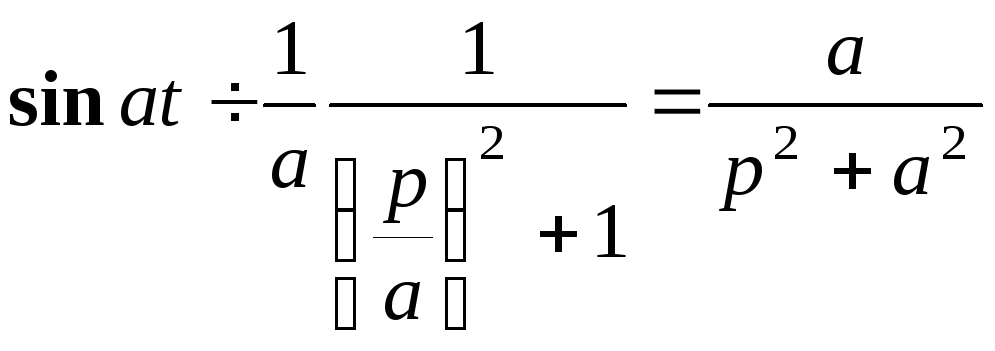Матан1-2(диффуры)
.doc
![]()
![]()
|
|
|
|
|
|
|
|
1 |
2 |
|
2 |
0 |
|
|
1 |
2 |
|
0 |
-1 |
|
|
1 |
2 |
|
1 |
-1 |
|
|
1 |
2 |
|
0 |
i |
|
|
1 |
2 |
|
1 |
i |
|
|
1 |
2 |
|
0 |
1 |
|
|
1 |
2 |
|
2 |
1 |
|
|
1 |
2 |
|
0 |
1+i |
|
|
0 |
1 |
|
2 |
0 |
|
|
2 |
2 |
|
0 |
2 |
|
|
2 |
2 |
|
1 |
2 |
|
|
i |
-i |
|
0 |
i |
|
|
2+i |
2-i |
|
0 |
2 |
|
|
2+i |
2-i |
|
0 |
2+i |
|
Теорема.
Если
![]() ,
то
,
то
![]() ,
где
,
где
![]() отвечает за
отвечает за
![]() ,
а
,
а
![]() отвечает за
отвечает за
![]() .
.
![]() - частное решение уравнения
- частное решение уравнения
![]() ,
а
,
а
![]()
![]() - частное решение уравнения
- частное решение уравнения
![]() .
.
Операционное счисление.
Понятие изображения и оригинала.
![]() -
оригинал.
-
оригинал.
-
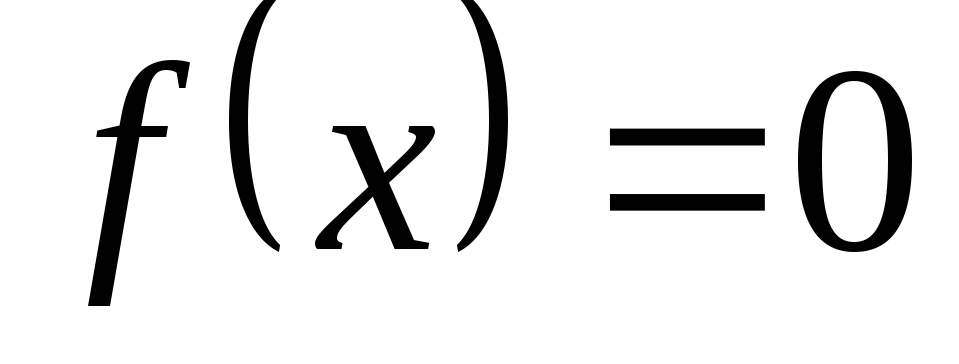 ,
если
,
если
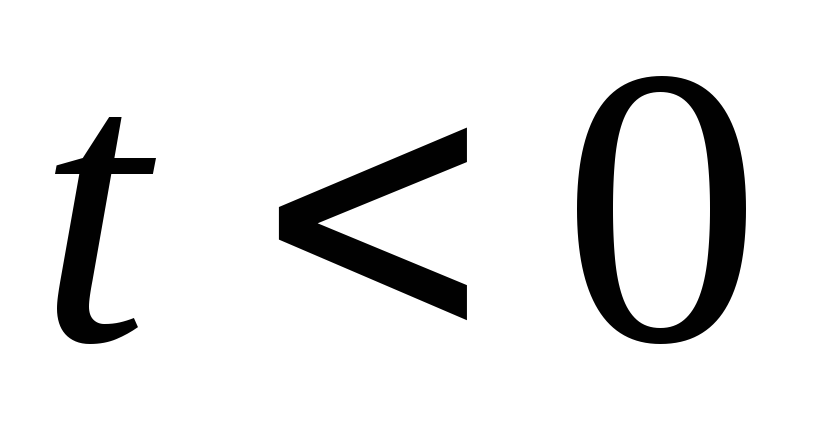
-
Кусочно-непрерывная.
-
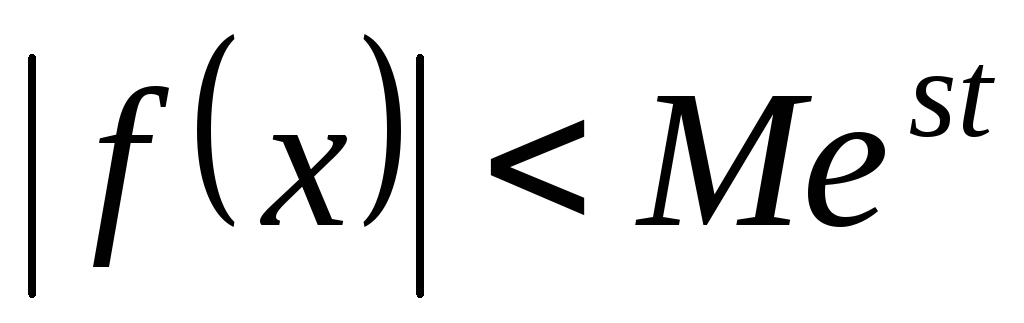 -
растет не быстрее чем показательная
функция.
-
растет не быстрее чем показательная
функция.
![]()
![]() -
произвольное комплексное число.
-
произвольное комплексное число.
![]() -
изображение
-
изображение
![]() ,
лапласово изображение, преобразование
Лапласа, трансформанта.
,
лапласово изображение, преобразование
Лапласа, трансформанта.
![]()
Теорема. О единственности.
Если
![]() ,
и
,
и
![]() ,
то
,
то
![]() .
.
Если
![]() ,
и
,
и
![]() ,
то
,
то
![]() .
.
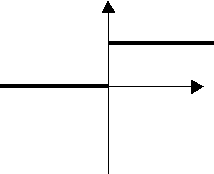
![]() -
функция Хевисайда.
-
функция Хевисайда.
![]()
![]()
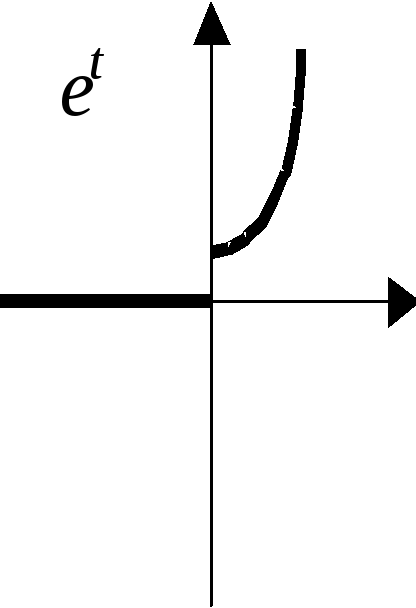
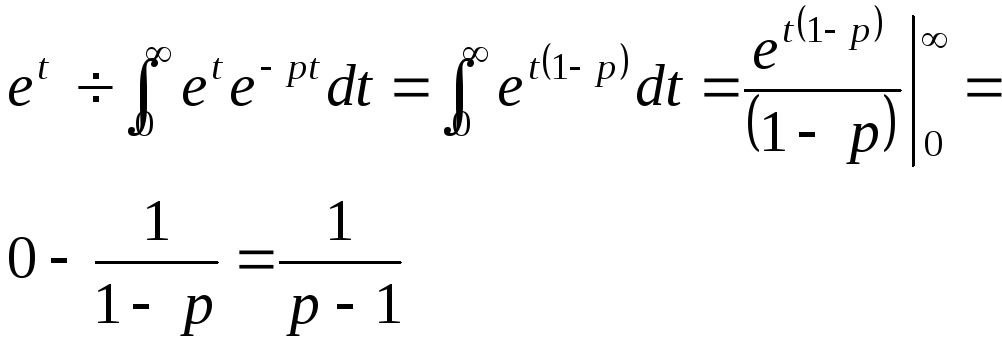
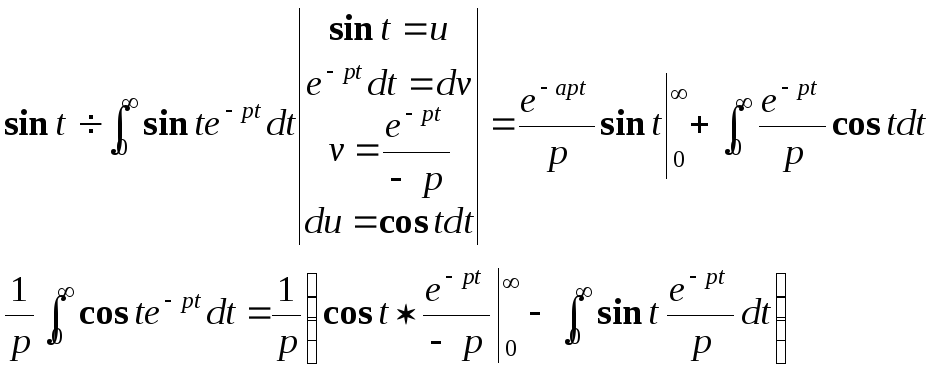

![]()
Свойства преобразования Лапласа.
Теорема. Линейности.
Если
![]() ,
и
,
и
![]() ,
то
,
то
![]() .
.
Изображение линейной комбинации равно линейной комбинации изображений
Постоянный множитель выносится за знак изображения.
Доказательство:
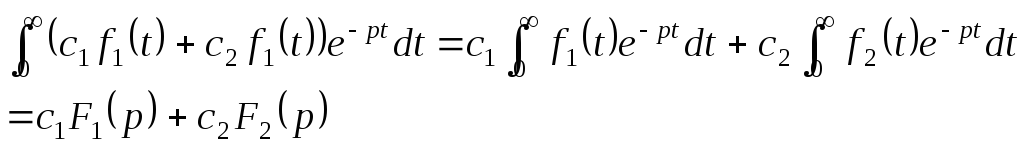
Пример:
1)
![]()
![]()
2)![]()
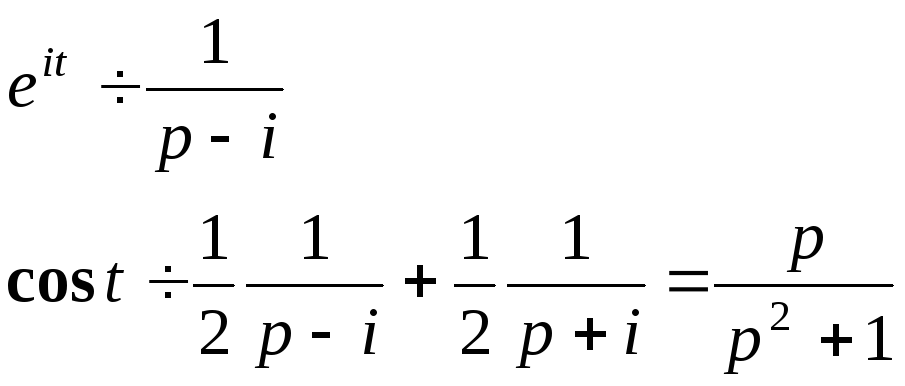
Теорема. Подобия

Доказательство:

Пример:

Теорема. Смещения.
![]()
Доказательство:
![]()
Пример:

Теорема. Дифференцирования оригинала.
![]()
Доказательство:
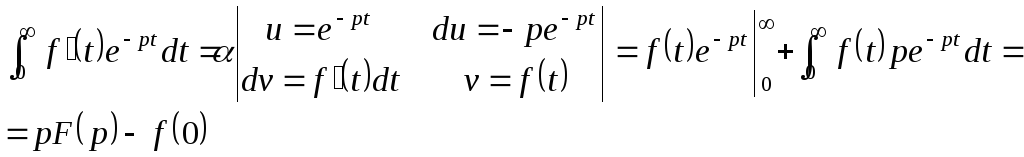
Пример:
![]()
Следствия:
![]()
Пример:

Теорема. Теорема о дифференцировании изображения (умножении)
![]()
Доказательство:
![]()
Пример:
Теорема. Об интегрировании оригинала.
![]()
Доказательство:

Пример:
Примеры:

![]()
![]()
Теорема. Деления (интегрирования изображения)
![]()
Если
![]() - оригинал и
- оригинал и
![]() - изображение
- изображение
![]() .
.
![]()
![]()
Пример:
![]()
Теорема. Запаздывания
![]()
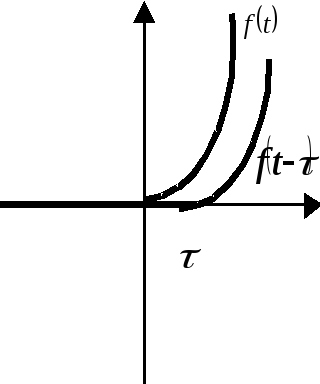
![]()

Пример:
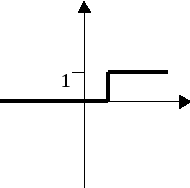
![]()
Сворачивание функций.
![]()
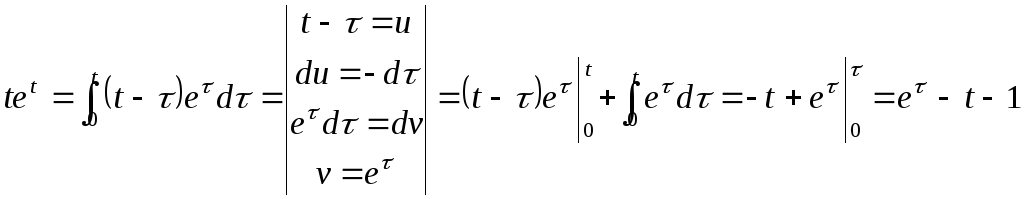
Теорема. О свертке.
![]()
![]()

=![]()
Дельта – функция Дирака.
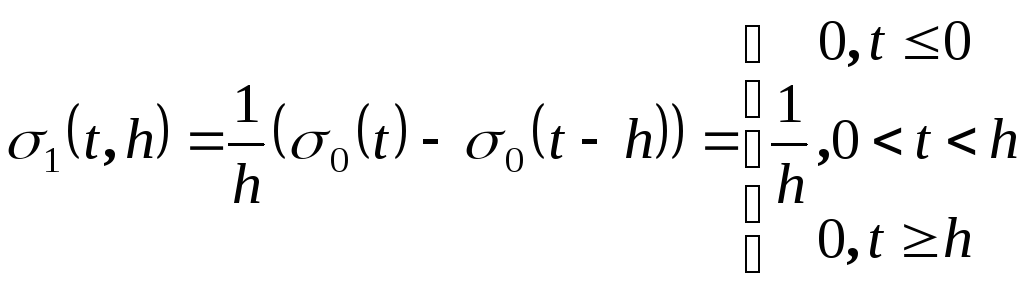

![]()
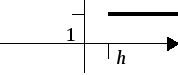
![]()

![]()
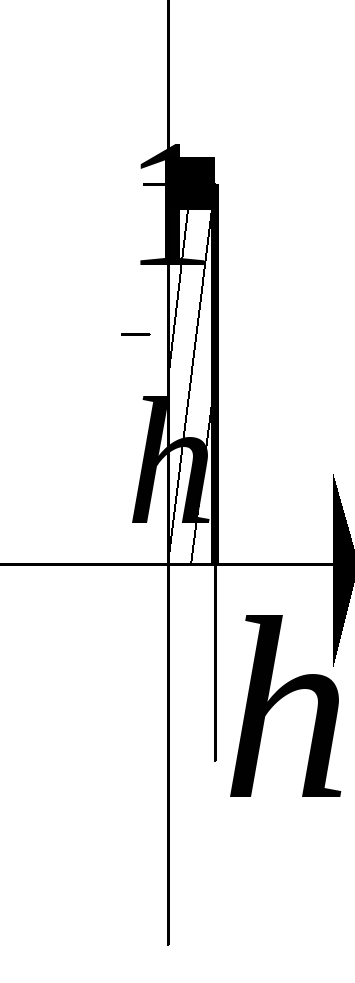
![]()
![]()
![]()
Решение дифференциальных уравнений операционным
методом.
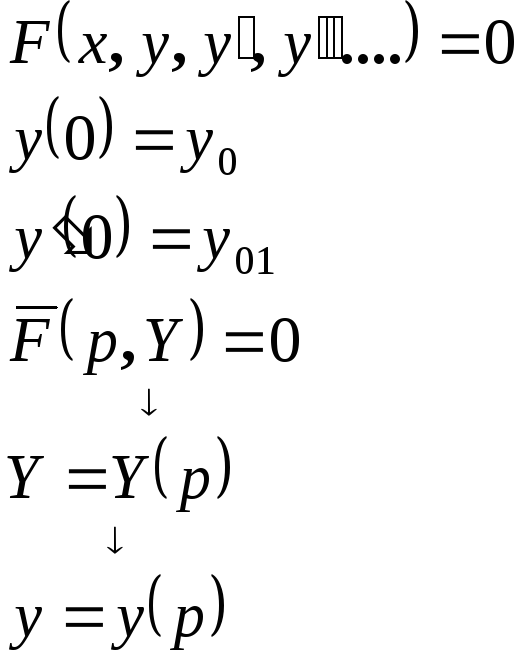
![]() -
неизвестная функция.
-
неизвестная функция.
1)
![]()
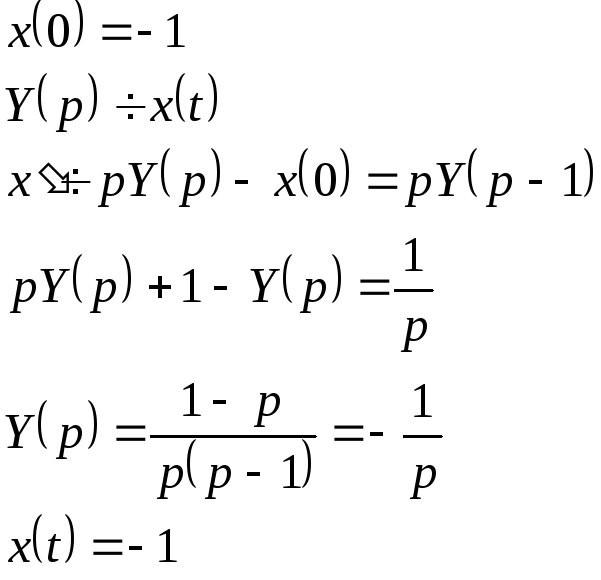
2)![]()
![]()
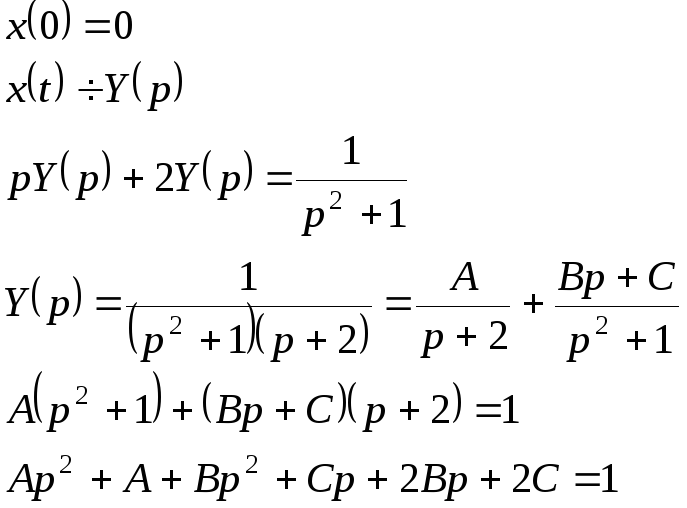
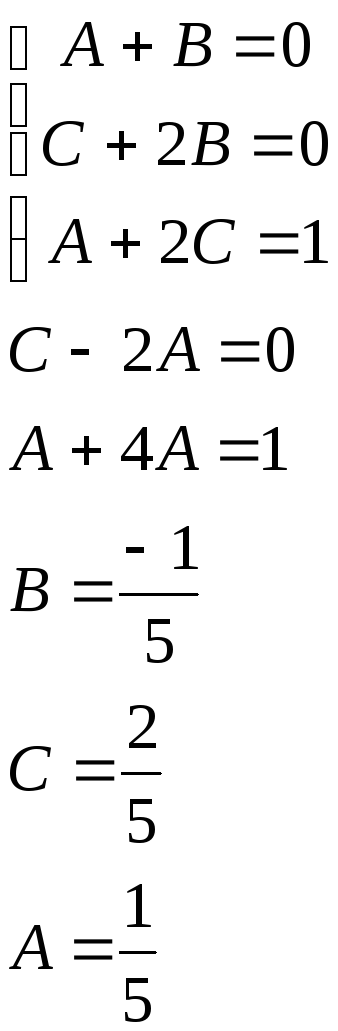


![]()
![]()
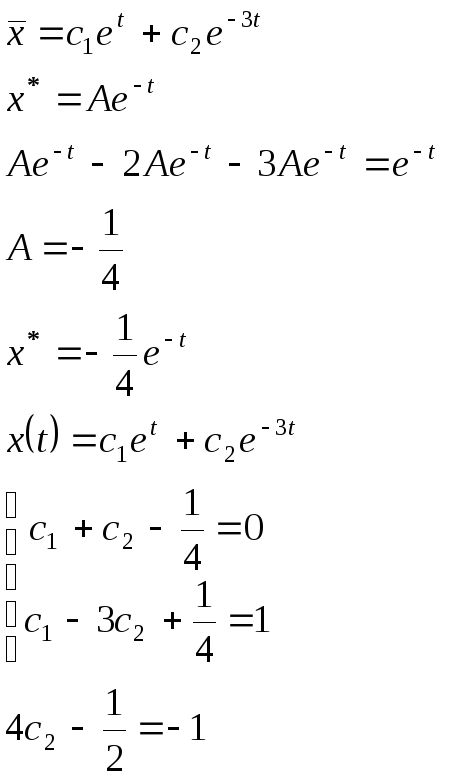


![]()
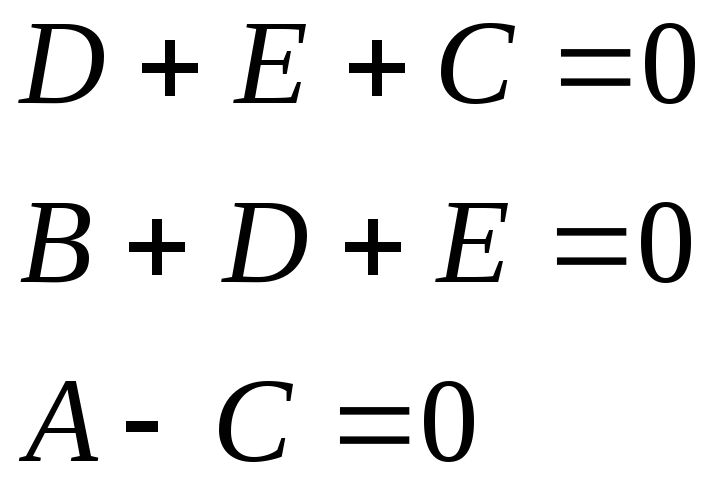
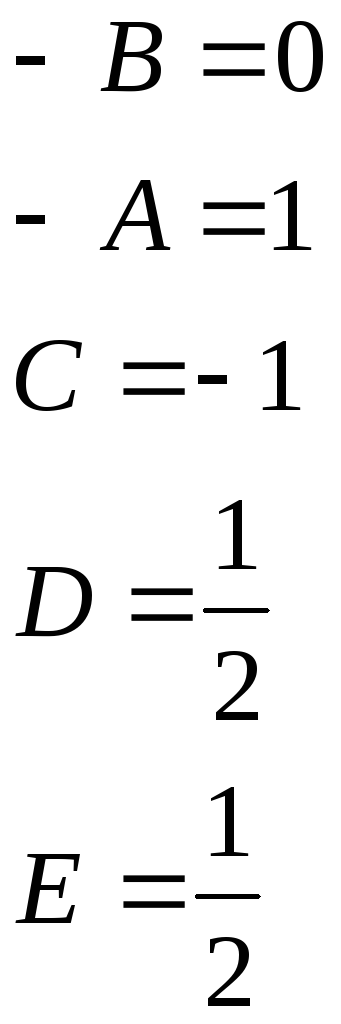
![]()
-
 ,
где
,
где
 задана
графически.
задана
графически.

![]()