
8111 практика 1-36 / Практика16.Ограниченность_функции;предел_функции
.pdf
Практика 16. Ограниченность функции; предел функции
16.1.Ограниченность функции
Определение 1. Функция f(x) называется о г р а н и ч е н н о й н а п р о м е ж у т к е X
или л о к а л ь н о о г р а н и ч е н н о й, если ограничено множество значений 1 этой функции при x 2 X, т. е.
9 m; M : 8 x 2 X m f(x) M:
Если X = D(f), то указание на множество X (соответственно, слово "локально\) опускают.
Определение 2. Точную верхнюю (нижнюю) грань множества значений функции f(x), x 2 D(f), называют в е р х н е й (н и ж н е й) г р а н ь ю функции и обозначают
M0 = supff(x)g = sup f(x) = sup f (m0 = infff(x)g = inf f(x) = inf f) :
Если рассматривают значения функции лишь на множестве X 2 D(f), то говорят о в е р х н е й (н и ж н е й) г р а н и функции на множестве X и пишут
M |
0 |
x2Xf |
f(x) |
g |
x2X |
X |
|
0 |
= x2Xf |
f(x) |
g |
x2X |
X |
|
|
= sup |
|
= sup f(x) = sup f |
m |
|
inf |
|
= inf f(x) = inf f |
: |
|||||
Пример 1. Показать, что функция
x2 f(x) = x4 + 9
является ограниченной.
Заметим, что D(f) = R. Очевидно, что2 f(x2) 0, т.е. функция ограничена снизу. |
|||||||
Воспользовавшись известным неравенством a |
+ b 2jajjbj, получим, что |
||||||
|
x2 |
x2 |
1 |
||||
f(x) = |
|
|
|
= |
|
|
|
x4 + 9 |
2 3 x2 |
6 |
|||||
функция ограничена сверху. |
|
|
|
|
x2 |
||
|
|
x2 |
|
|
|
|
|
Вывод: 9 m = 0; M = 1=6 : 8 x m x4 + 9 M; ò. å. f(x) = x4 + 9 ограниченная.
Пример 2. ( 385) Исследовать на ограниченность функцию
f(x) = ln x sin2 x
âинтервале (0; ").
Òàê êàê 0 sin2 x 1, а функция ln x монотонно возрастающая и ограничена сверху нулем, если 0 < " 1, и числом ln ", если " > 1, то f ограничена сверху:
f(x) maxf0; ln "g:
1Можно написать определения локально ограниченной функции снизу, сверху аналогично определениям ограниченных множеств в лекции 3.
1

О. А. Кузенков, Е. А. Рябова |
2 |
|
|
Поскольку ln x в окрестности нуля не ограничен снизу, можно предположить, что и
f(x) в интервале (0; ") снизу не ограничена: 8 m > 0 9 xm 2 (0; ") : 2 |
f(xm) < m |
||||||||||||||
Далее, выберем последовательность значений |
xn так, чтобы sin |
x = 1 è xn 2 (0; "), |
|||||||||||||
например, xn = |
2 |
. Тогда, начиная с некоторого номера n0 âñå xn попадают в интервал |
|||||||||||||
1 + 2n |
|||||||||||||||
(0; "). При этом для любого m > 0 |
|
|
|
|
|
1 + 2n |
< ln n < m |
||||||||
|
f(xn) = ln 1 + 2n = ln 2 ln(1 + 2n) = ln 2 ln 2n ln |
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
||
ïðè n > em, в том числе для n = nm = maxf[em] + 1; n0g. |
|
|
|
|
|
||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
8 m > 0 |
9 nm = maxf[em] + 1; n0g : |
xnm = |
2 |
|
2 (0; "); |
|
f(xnm) < m; |
|||||||
|
|
|
|
|
|||||||||||
|
1 + 2nm |
|
|||||||||||||
т. е. f(x) не ограничена снизу. |
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3. ( 385) Показать, что функция |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
f(x) = |
x |
; |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 + x |
|
|
|
|
|
|||
в области 0 x < +1 имеет н и ж н ю ю |
ã ð à í ü m0 = 0 è â åxð õ í þ þ ã ð à í ü M0 = 1. |
||||||||||||||
|
Чтобы доказать, что m |
0 |
= 0 |
|
|
[0;+1) |
|
|
|
|
|||||
|
|
1+x |
|
||||||||||||
|
|
, надо доказать, что inf |
= 0, ò. å. |
||||||||||||
1.8 x 2 [0; +1) 1+xx 0;
2.8 " > 0 9 x 2 [0; +1) : 1+xx < ":
Первое условие, очевидно, выполняется. Далее, для произвольного " 2 (0; 1) неравен-
ñòâî 1+xx < " имеет место при 0 x < 1 " " , следовательно, и второе условие выполняется. Значит, m0 = 0.
Аналогично, чтобы доказать, что M0 = 1, надо доказать, что sup x = 1, ò. å.
1+x
[0;+1)
1.8 x 2 [0; +1) 1+xx 1;
2.8 " > 0 9 x 2 [0; +1) : 1+xx > 1 ":
Первое условие, очевидно, выполняется. Далее, для произвольного " 2 (0; 1) неравен-
ñòâî 1+xx > 1 " имеет место при x > 1 " " , следовательно, и второе условие выполняется. Значит, M0 = 1.
16.2.Предел функции: определение по Гейне
Определение 3. Точка a п р е д е л ь н а я точка множества X, если в любой "- окрестности точки a содержится хотя бы одна точка из X, не совпадающая с a. При этом точка a может принадлежать X; а может и не принадлежать.
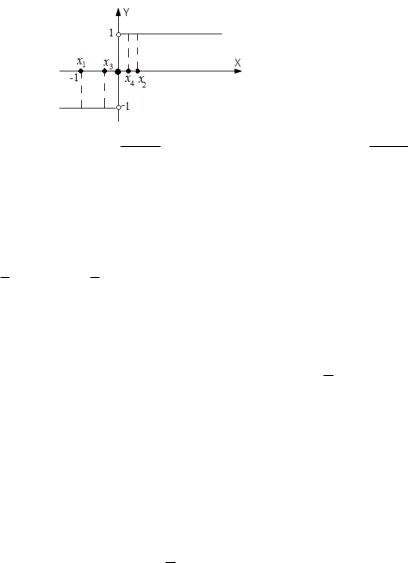
Пример 4. Рассмотрим функцию f(x) на области определения X (ðèñ. 1). Пусть x = aпредельная точка множества X, не принадлежащая этому множеству. Выберем какуюнибудь последовательность значений fxng, сходящуюся к a, xn 6= a. Видим, что соответствующие значения fyng рассматриваемой функции при этом сходятся к числу A.
Очевидно, что в этом примере для любой последовательности значений fxng из множества X такой, что xn ! a ïðè n ! 1, xn 6= a, соответствующая последовательность значений функции fyng будет сходится к A.

О. А. Кузенков, Е. А. Рябова |
3 |
|
|
Рис. 1: На оси Ox отмечены члены последовательности fxng, на оси Oy члены ff(xn)g.
Определение 4. Число A называется пределом функции f в точке a п о Г е й н е, если
1.a предельная точка области определения функции f;
2.для каждой последовательности точек fxng из области определения функции f, сходящихся к a и отличных от a, последовательность ff(xn)g значений функции сходится к A, т. е.
|
|
A = lim f(xn): |
|
|
|
|
|
n!1 |
|
|
|
В этом случае пишут |
|
|
|
|
|
A |
lim f(x) |
èëè f x |
A ïðè x |
! |
a: |
|
= x a |
( ) ! |
|
|
|
|
! |
|
|
|
|
Вместо предел функции в точке a говорят также предел функции при x ! a .
Определение предела функции по Гейне называют также определением н а я з ы к е п о с л е д о в а т е л ь н о с т е й.
Èç определения 4 и единственности предела последовательности следует, что функция не может иметь двух различных пределов в одной точке.
x2 16
Пример 5. Найти предел функции f(x) = x2 4x в точке x = 4.
Область определения этой функции X = fx : x 2 R; x 6= 0; x 6= 4g. Точка x = 4 является предельной точкой этого множества, так как в любой "-окрестности этой точки содержатся точки из X, не совпадающие с x = 4.
Воспользуемся определением по Гейне предела функции в точке. Будем рассматривать данную функцию в некоторой окрестности точки x = 4, например, на интервале (3; 5).
Возьмем какую-либо последовательность fxng такую, что xn 2 (3; 5), xn 6= 4 è lim xn = 4.
n!1
Тогда на основании теорем о пределах последовательностей имеем
|
|
2 |
16 |
|
xn + 4 |
|
lim xn + 4 |
|
||
lim f(xn) = lim |
xn |
= lim |
= |
n!1 |
= 2: |
|||||
|
|
xn |
|
|||||||
n!1 |
n!1 xn2 |
|
4xn |
n!1 |
|
lim xn |
|
|||
|
|
|
|
|
|
|
|
n!1 |
|
|
В силу произвольности выбранной последовательности fxng, согласно определению по
Гейне предела функции в точке
lim x2 16 = 2:
x!4 x2 4x
О. А. Кузенков, Е. А. Рябова |
4 |
|
|
Из определения по Гейне предела функции в точке вытекает
Следствие 16.1. Если существуют последовательности fxng è fxng точек из области определения функции f, сходящихся к точке a и отличных от a, для которых последовательности ff(xn)g è ff(xn)g соответствующих значений функции сходятся к разным пределам или хотя бы одна из них расходится, то функция при x ! a предела не имеет.
Пример 6. Доказать, что функция f(x) = sgn x (ðèñ. 2) не имеет предела в точке x = 0.
|
1)n |
( |
1)n |
|
|
Рис. 2: На оси Ox отмечены члены f |
( |
g, на оси Oy члены fsgn |
|
|
g. |
n |
|
n |
|||
Область определения этой функции X = R. Точка x = 0 является предельной точкой этого множества, так как в любой "-окрестности этой точки содержатся точки из X, не совпадающие с x = 0.
Возьмем две последовательности fxng è fxng точек из X, сходящихся к точке x = 0
11
èотличных от 0: xn = n è xn = n. Соответствующие последовательности ff(xn)g è ff(xn)g являются стационарными: f(xn) = 1, f(xn) = 1 и сходятся одна к едини-
це, другая к минус единице. Значит, предел функции f(x) = sgn x в точке x = 0 не существует.
Доказать, что не существует предел функции f(x) = cos x в точке x = 0.
Заметим, что x = 0 предельная точка D(f). Выберем последовательности fxng, fxng, сходящиеся к 0 и отличные от 0, так, чтобы f(xn) = 1, f(xn) = 0.
Нетрудно видеть, что последовательности
xn = |
1 |
|
; xn = |
2 |
|
; n 2 N; |
2n |
1 + 2n |
|||||
удовлетворяют этим требованиям. Соответствующие им последовательности ff(xn)g è
ff(xn)g значений функции стационарные и сходятся к разным значениям. Это доказывает отсутствие предела функции f(x) = cos x в точке x = 0.
16.3.Арифметические свойства предела функции
Благодаря определению 4 предела функции на языке последовательностей арифмети- ческие свойства предела последовательности легко переносятся на случай предела функции.
Теорема 16.1. Пусть для функций f(x) è g(x) существуют пределы lim f(x) è lim g(x):
x!a x!a

О. А. Кузенков, Е. А. Рябова |
|
|
|
|
|
|
|
|
5 |
|
|
|
|||||||||
Тогда существуют указанные ниже пределы и справедливы равенства |
|
|||||||||
lim (f(x) |
|
g(x)) = lim f(x) |
|
lim g(x); |
(1) |
|||||
x!a |
|
x!a |
x!a |
|
||||||
lim (f(x) |
|
g(x)) = lim f(x) |
|
lim g(x); |
(2) |
|||||
x |
! |
a |
|
x |
! |
a |
! |
|
||
|
|
|
x a |
|
||||||
если, кроме того, lim g(x) 6= 0, òî
x!a
lim f(x)
x!a g(x)
Пример 8. ( 411 а, б) Найти
|
lim f(x) |
|
|
= |
x!a |
: |
(3) |
|
lim g(x) |
|
|
x!a
a) lim |
x2 1 |
; á) lim |
x2 1 |
: |
|
2x2 x 1 |
2x2 x 1 |
||||
x!0 |
x!1 |
|
а) Применяя теоремы о пределе алгебраической суммы (1) и произведения (2), находим предел знаменателя
x!0 |
2 |
|
|
1 = |
x!0 |
x!0 |
x!0 |
x!0 |
x!0 |
|
|
lim |
x2 |
|
x |
|
lim 2 |
lim x |
lim x |
lim x |
lim 1 = |
|
1: |
Предел знаменателя не равен нулю, поэтому по теореме о пределе частного (3) получаем
|
x |
2 |
1 |
|
|
|
lim (x2 |
|
1) |
|
1 |
|
|||||
lim |
|
|
= |
|
x!0 |
|
|
= |
= 1: |
||||||||
2x2 |
|
1 |
|
|
|
||||||||||||
x!0 |
|
x |
|
|
lim (2x2 |
|
x |
|
1) |
|
1 |
|
|||||
|
|
|
|
|
x |
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
б) Здесь числитель и знаменатель стремятся к нулю:
lim |
|
x2 |
1 = 0 |
è lim |
x2 |
|
x |
1 |
; |
x!1 |
|
x!1 |
2 |
|
= 0 |
т. е. имеет место неопределенность вида 00. Теорема о пределе частного (3) непосредственно неприменима.
Äëÿ "раскрытия неопределенности\ надо сократить в числителе и знаменателе одина- ковый сомножитель (x 1), èç-çà которого мы и имеем эту неопределенность. Обратим
внимание, что x 1 6= 0 при x ! 1, так как x "близко\ к единице, но x 6= 1. Разделив числитель и знаменатель на (x 1), получим при x 6= 1 равенство
x2 1 |
= |
x + 1 |
: |
|
|
||
2x2 x 1 2x + 1 |
|
||
Так как lim (2x + 1) = 0, то по теореме о пределе частного (3) найдем |
||||||||||||||||
x!1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
1 |
|
|
x + 1 |
|
|
lim(x + 1) |
|
2 |
|
|||
|
lim |
|
|
= lim |
= |
x!1 |
= |
: |
||||||||
|
2x2 |
|
|
|
|
|
|
|||||||||
|
|
|
1 |
2x + 1 |
3 |
|||||||||||
|
x!1 |
|
x |
|
x!1 |
|
lim(2x + 1) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
16.4.Задачи для самостоятельной работы
383, 384, 387, 390, 412, 414, 419, 420;
Для функции f(x) из задачи 384 доказать, что не существует lim f(x), используя
x!0
следствие 16.1.
